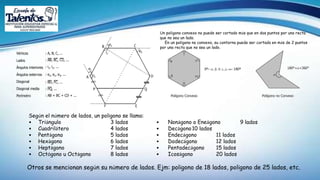
Este documento trata sobre polígonos y su relación con la prevención del Covid-19. Explica qué tipos de polígonos se pueden usar para representar zonas de contagio y cómo los polígonos se pueden relacionar con la vida personal. Luego define los diferentes tipos de polígonos según el número de lados y sus propiedades. Finalmente, propone un ejemplo de cómo dos personas que se encuentran podrían formar un polígono de entre 7 y 9 lados.

1. Polígonos
Sesión
2
Campo Temático:
• Regiones de Contagio
• Problemas Casuísticos
• Prevención

2. • ¿Qué tipo de figuras poligonales se relaciona con los casos de contagio?
• ¿Qué representaciones poligonales se pueden identificar con las zonas de contagio en lima metropolitana?
• ¿como se relaciona los polígonos en la vida personal?

3. Retroalimentación
REPASO DEL TEMA ANTERIOR
¿Qué aspectos importantes
recordamos del tema de triángulos?
¿Cómo aplicó el campo temático
comprendido, ante las figuras
poligonales?

5. Polígono Cronológico de Prevención del Covid - 19

6. Un polígono convexo no puede ser cortado más que en dos puntos por una recta
que no sea un lado.
En un polígono no convexo, su contorno puede ser cortado en más de 2 puntos
por una recta que no sea un lado.





0º 180º
Polígono Convexo


Polígono no Convexo
180°< <360°
Según el número de lados, un polígono se llama:
• Triángulo 3 lados • Nonágono o Eneágono 9 lados
• Cuadrilátero 4 lados • Decágono10 lados
• Pentágono 5 lados • Endecágono 11 lados
• Hexágono 6 lados • Dodecágono 12 lados
• Heptágono 7 lados • Pentadecágono 15 lados
• Octógono u Octágono 8 lados • Icoságono 20 lados
Otros se mencionan según su número de lados. Ejm: polígono de 18 lados, polígono de 25 lados, etc.

7. e
c
O
i
O centro
c ángulo central
e ángulo exterior
i ángulo interior
i i
i
e
1. Equilátero
Tiene todos sus lados congruentes.
2.Equiángulo
Tiene todos sus ángulos congruentes.
i: ángulo interior
e: ángulo exterior
3.Regular
Tiene sus lados congruentes y sus ángulos también congruentes.
Propiedades
1. En todo polígono, el número máximo de diagonales que se pueden trazar desde un
vértice es:
(n - 3) diagonales

8. N =D
n(n - 3)
2
N =DM
n(n - 1)
2
2. En todo polígono el número de diagonales es igual a:
3. El número de diagonales medias de todo polígono es
igual a:
sinteriores = 180º(n - 2)
 externos = 360ºs
4. La suma de los ángulos internos de todo polígono convexo, es igual a:
5. La suma de los ángulos externos de todo polígono convexo es:
6. En un polígono convexo, al trazar todas las diagonales desde 1 solo vértice se forman:

9. Desarrollo del Campo temático

10. Dos personas caminan de manera rectilíneo, si la mujer hace un menor recorrido
hacia P y el hombre realiza el mayor recorrido para dar el encuentro a la mujer
en el punto.
Considerando que cualquiera que llega antes espera a la otra persona, será cierto
afirma que las direcciones rectilíneas que recorren cada uno pueden formar un
polígono de 7, 8 y 9 lados

11. Prevención

12. Metacognición
• ¿ Qué comprendí ?
• ¿Cuál es su opinión sobre el
campo temático tratado?
• ¿Cómo describiría Ud. el
significado del triangulo
cronológico?
• ¿Cómo aplicaría Ud. en su práctica
directiva, el campo temático que
ha comprendido?

13. Recursos Títulos
Libros de Lecturas Links
PDF Enciclopedia Virtual
PDFs
Link
Recursos a utilizar

14. GRACIAS