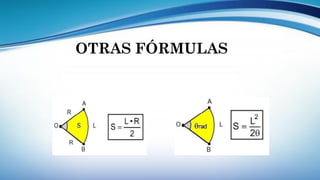
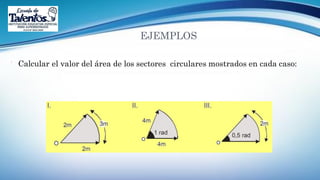
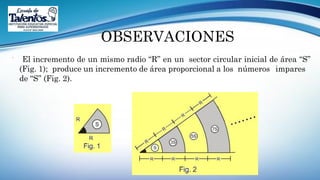
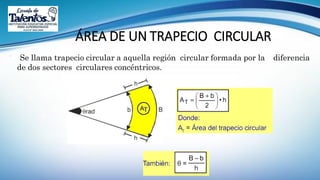
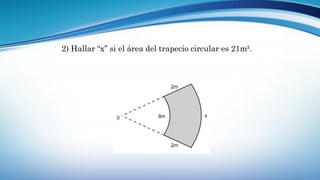
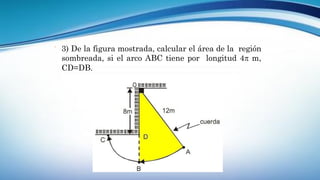
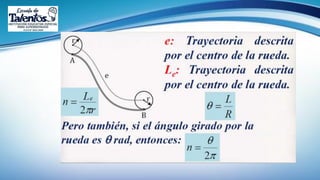
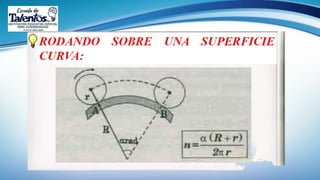
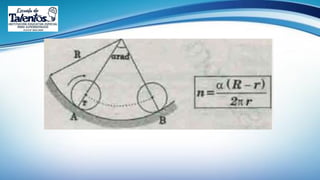
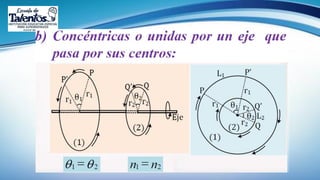
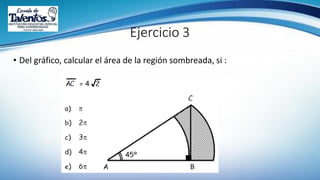
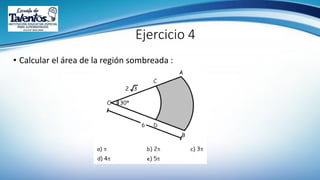
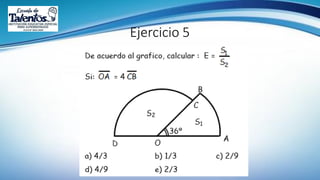
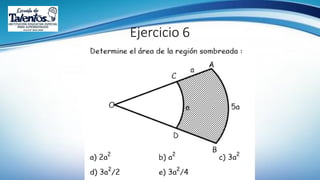
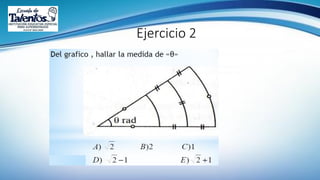
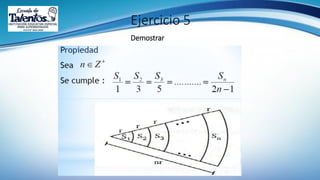
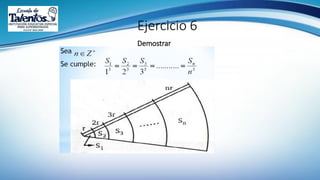
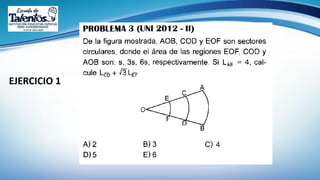
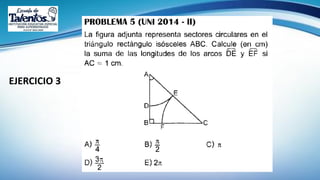
Este documento trata sobre la longitud de arco y el sector circular en trigonometría. Explica que la longitud de arco se calcula multiplicando el número de radianes por el radio de la circunferencia. Un sector circular es la región limitada por dos radios y el arco correspondiente, y su área es igual al producto del cuadrado del radio por la medida del ángulo central en radianes. Finalmente, presenta ejemplos de aplicaciones como el diseño de estructuras y el cálculo del área requerida para asfaltar una curva en una calle