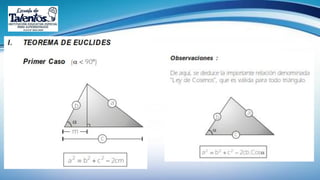
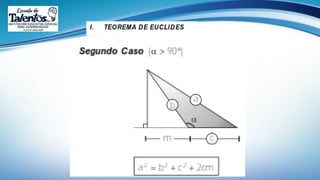
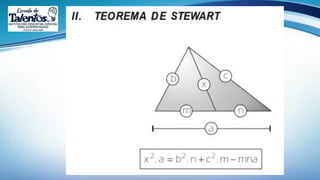
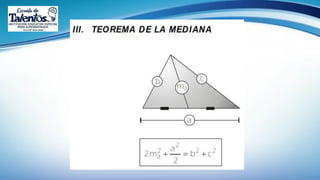
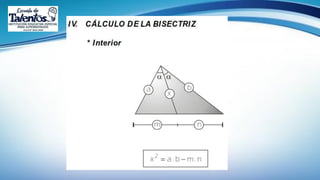
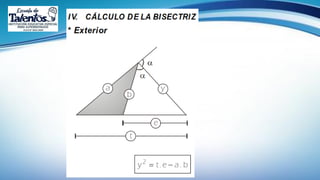
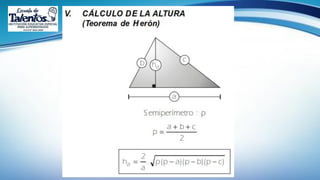
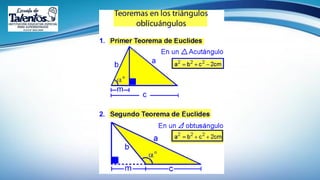
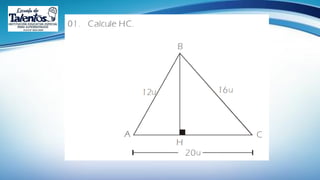
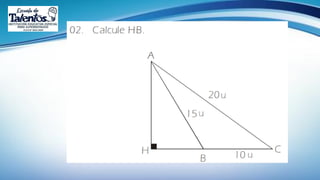
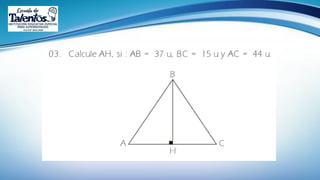
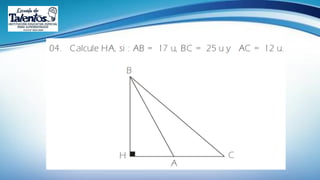
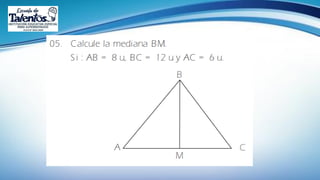
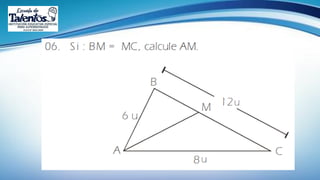
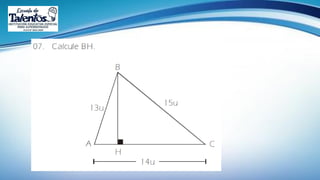
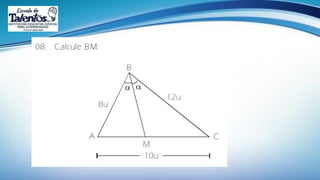
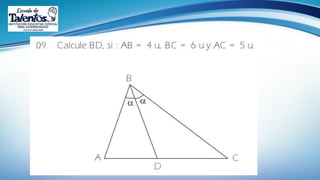
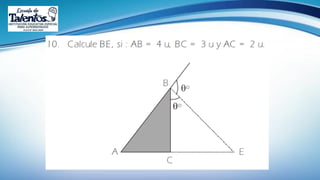
Este documento trata sobre las relaciones métricas en cualquier triángulo. Explica conceptos como triángulos oblicuángulos y obtusángulos, y cómo realizar proyecciones ortogonales y de segmentos de recta. Incluye problemas de aplicación y prevención sobre el Covid-19, así como una sección de metacognición y emprendimiento relacionados con este tema.

1. Relaciones Métricas en
Cualquier Triángulo
Sesión
12
Campo Temático:
• Proyección
• Problemas Casuísticos
• Prevención

2. ¿Quéformasobservas?

3. • 1) ¿Qué entendemos por triangulo oblicuángulo?
• 2) ¿Qué entendemos por triangulo obtusángulo?
• 3) ¿Cómo se lleva a cabo la proyección ortogonal de un punto sobre una recta?
• 4) ¿Cómo se lleva a cabo la proyección de un segmento de recta cualquiera en el espacio sobre
una recta?
• 5) diseño de productos apoyados en proyecciones

5. Retroalimentación
REPASO DEL TEMA ANTERIOR
¿Qué aspectos importantes
recordamos del tema de relaciones
métricas en triángulos rectángulos?.
¿Cómo aplico el campo temático
comprendido, ante las relaciones
geométricas?

7. Campo Temático:
Sesión 12
Relaciones Métricas
en Cualquier
Triángulo
-Semejanza
-Proporcionalidad
-Tipos de Triángulos
-Problemas Casuísticos
-Prevención y Curación

8. Forma Geométrica del Virus Covid 19
Razones y Proporcionalidad

9. Desarrollo del Campo temático

10. Proyeccioneslaterales

11. Relaciones
Métricas en
Cualquier
Triángulo

21. APLICACIÓN REAL DE LAS
RELACIONES METRICAS
EN TRIANGULOS
OBLICUANGULOS

22. Problema No 1
• Hallar la longitud del faro inclinado si se sabe que en el triangulo ABC
que se observa el lado “b” mide 9.9m, los ángulos A, B miden 42° y
53° respectivamente.

23. Problema No 2
Hallar la distancia que existe entre el paquete y el obrero en el instante que en el
triangulo ABC se cumpla que A=37°, B=80°, a=4.5m y c=7.2m

24. Problema No 3
• Una persona de 1.8 metros de estatura camina en la noche en línea
recta a una velocidad de 2.5 m/s. Si pasa junto a un árbol de 6 metros
de altura. Obtener la velocidad del extremo de la sombra que se
genera sobre la calle después de 3 segundos.

25. RELACIONES METRICAS
EN CUALQUIER
TRIANGULO
TEST DE APRENDIZAJE PREVIO

36. Prevención

37. QUÉDATE EN CASA
SALVA VIDAS.
• Ayuda a frenar el coronavirus
• 1. QUÉDATE en casa lo máximo posible
• 2. MANTÉN el distanciamiento social
• 3. LÁVATE las manos con frecuencia
• 4. TOSE cubriéndote con el codo
• 5. LLAMA si tienes síntomas

38. Metacognición
• ¿ Qué comprendí?
• ¿Cuál es su opinión sobre el
campo temático tratado?
• ¿Cómo describiría Ud. el
significado de relaciones métricas
en cualquier triángulo?
• ¿Cómo aplicaría Ud. en su práctica
directiva, el campo temático que
ha comprendido?

39. Emprendimiento
• ¿Cómo aplicaría Ud. en la vida
diaria, los conceptos de las
relaciones métricas en
cualquier triángulo?
• Si desea innovar alguno de los
productos mostrados. ¿Cuál
seria su propuesta?

40. Recursos Títulos
Libros de Lecturas Links
PDF Enciclopedia Virtual
PDFs
Link
Recursos a utilizar

41. GRACIAS