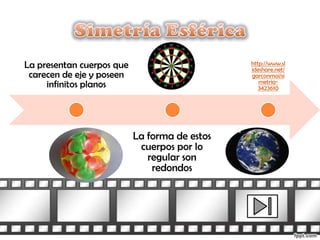
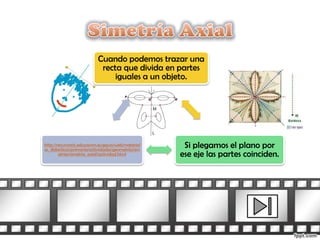
Este documento trata sobre las transformaciones geométricas de simetría. Explica diferentes tipos de simetría como la simetría axial, la simetría central y la simetría reflectiva. También describe propiedades como la conservación de ángulos, distancias y colinealidad bajo transformaciones como rotaciones y traslaciones. El documento incluye ejemplos interactivos para practicar y evaluar el conocimiento sobre estas transformaciones.

2. Lección: La simetría
• Tema: Transformaciones.
• Subtema: Movimientos en el plano y transformaciones
rígidas.
• Conocimientos y habilidades: En esta lección
determinarás las propiedades de la rotación y traslación
de figuras.
• Eje: Forma, espacio y medida.

3. Simetría
Esférica
Reto
Simetría
Axial
Definición
Propiedades
Simetría
Nota: Para conocer Reflectiva
mas acerca de este
tema presiona Simetría
sobre cada de
nombre. Traslación

4. • Simetría…del
latín symmetrĭa
• Cada eje de simetría
• La simetría supone divide a las figuras en
equilibrio unas partes llamadas
planos

5. La presentan cuerpos que http://www.sl
ideshare.net/
carecen de eje y poseen garconmoi/si
metria-
infinitos planos 3423610
La forma de estos
cuerpos por lo
regular son
redondos

6. Cuando podemos trazar una
recta que divida en partes
iguales a un objeto.
http://recursostic.educacion.es/gauss/web/material
es_didacticos/primaria/actividades/geometria/sim
Si plegamos el plano por
etrias/simetria_axial/actividad.html ese eje las partes coinciden.

7. Una mitad es el http://www.disfrutalasm
reflejo de la atematicas.com/geomet
ria/simetria-
otra mitad reflectiva.html
Puede ir
en cualquier
dirección

8. Todos los
puntos de
Movimiento una figura se
en el plano mueven en la
misma
dirección
http://es.scribd.
Se toma com/doc/7002
como base 0744/Simetria-
un vector Rotacion-y-
Traslacion

9. Colinealidad Distancias
Ángulos

10. Se conserva la Colinealidad, es decir, si hay puntos
alineados, en figuras resultantes también lo estarán.

11. Se conservan las
distancias. No
aumentan ni
disminuyen las
distancias del original
a la copia

12. Se conservan las
medidas de los ángulos.
No crecen ni decrecen.

13. Carolina trabaja en un despacho de publicidad, donde tiene que diseñar
un logotipo para uno de los clientes más importantes del despacho, la
empresa “Munguía y asociados”. Son clientes muy exigentes. Por ello han
puesto instrucciones específicas para realizar el logotipo: debe dibujar, en
los cuadrantes restantes figuras simétricas a la que ya está en el segundo
cuadrante respecto a los ejes x, y del plano cartesiano. Es un trabajo muy
importante, por lo que Carolina solicita tu ayuda. ¿Puedes ayudarla?
Aceptas el NO Aceptas
reto el reto

14. Un nuevo reto: Después de que observaste y trazaste figuras usando simetría,
traslación o rotación, debes pasar excelentemente el siguiente reto.
•Instrucciones: Da un clic en el circulo de F si la afirmación es falsa y en el circulo
de V si es verdadera.
2.- Las rectas se vuelven “curvas”
1.- En una reflexión los ángulos
cuando les aplicas una simetría
crecen.
central.
F V F V
3.-En las simetrías, rotaciones, 4.-En las traslaciones se necesita
reflexiones y traslaciones se forzosamente un vector que indique
conservan las longitudes de los dirección y magnitud.
ángulos.
F V F V

15. •Instrucciones: Da un clic en la palabra que indica la respuesta correcta.
1.-Esta simetría nos explica que en cada punto de la figura original existe otro
punto simétrico a la misma distancia del eje y en sentido contrario.
Rotación Traslación Simetría Axial Simetría Central
2.-En esta acción la figura original es un número de grados determinados,
alrededor de un punto fijo que puede estar dentro, sobre o fuera de la figura.
Rotación Traslación Simetría Axial Simetría Central
3.- Este es un caso especial de rotación, en el que a la figura original se le aplica
una rotación de 180 por un punto el cual puede estar, dentro, sobre o fuera de
la figura.
Rotación Traslación Simetría Axial Simetría Central

16. • En una reflexión los ángulos NO crecen,
mantienen su amplitud.

17. • En una reflexión los ángulos NO crecen,
mantienen su amplitud.

18. • Las rectas NO se vuelven “curvas” cuando
les aplicas una simetría central.

19. • Las rectas NO se vuelven “curvas” cuando
les aplicas una simetría central.

20. • 3.-En las simetrías, rotaciones, reflexiones y
traslaciones SI conservan las longitudes de
los ángulos.

21. • 3.-En las simetrías, rotaciones, reflexiones y
traslaciones SI conservan las longitudes de
los ángulos.

22. • 4.-En las traslaciones SI se necesita
forzosamente un vector que indique
dirección y magnitud.

23. • 4.-En las traslaciones SI se necesita
forzosamente un vector que indique
dirección y magnitud.

24. • La simetría axial nos explica que en cada
punto de la figura original existe otro
punto simétrico a la misma distancia del
eje y en sentido contrario.

25. • Es la simetría axial la que nos explica que
en cada punto de la figura original existe
otro punto simétrico a la misma distancia
del eje y en sentido contrario.

26. • En la acción de rotación es donde la figura
original es un número de grados
determinados, alrededor de un punto fijo que
puede estar dentro, sobre o fuera de la figura.

27. • En la acción de rotación es donde la figura
original es un número de grados
determinados, alrededor de un punto fijo que
puede estar dentro, sobre o fuera de la figura.

28. • La simetría central es un caso especial de
rotación, en el que a la figura original se le
aplica una rotación de 180° por un punto el
cual puede estar, dentro, sobre o fuera de la
figura.

29. • Es la simetría central es un caso especial de
rotación, en el que a la figura original se le
aplica una rotación de 180° por un punto el
cual puede estar, dentro, sobre o fuera de la
figura.

30. ¿Crees que también puedes usar algún tipo de traslación?
Finalmente el logotipo quedo así:
¿Qué tipo de simetría usarás?
•Si dijiste simetría de reflexión estas en lo
•Si la trasladas (la recorres) hacia
correcto, te puedes ayudar colocando un espejo
la derecha o hacia abajo sin
sobre cada uno de los ejes para ver cómo debe
moverla de posición hasta que
quedar la figura simétrica conforme la vas
trazando.
quede bien ubicada en otro
•Si dijiste simetría central (girando la figura 180˚)
cuadrante y la vuelves a
también es correcto, si bajas el dibujo original
reproducir otra vez con ayuda el
colocas otra hoja, la reproduces usando papel
carbón, posteriormente la clavas con una
logotipo quedara listo?
tachuela (o algo similar) en el origen del plano,
giras la hoja del dibujo hasta que quede en
sentido contrario y la vuelves a reproducir con
ayuda del papel carbón trazaras también el logo.
Para Contesta las Entrega a tu
comenzar el preguntas en maestro el
reto da un clic. tu cuaderno. logotipo final.

32. • Entrega a tu maestro tus respuestas o en su
caso el logotipo.
• Si aun sigues teniendo dudas, hazle saber al
tu maestro cuales son.

33. Stephanie Haydee Gizeh Claudia
Fernández Juárez Munguía Reynoso
Suarez Berriel. Jiménez. Rodríguez.