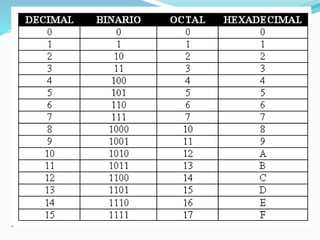
El documento habla sobre los sistemas de numeración, incluyendo el sistema decimal (base 10), binario (base 2), octal (base 8) y hexadecimal (base 16). Explica que los sistemas de numeración utilizan símbolos llamados cifras y están basados en una base determinada. También describe los métodos para convertir entre sistemas de numeración usando el teorema fundamental de la numeración y divisiones sucesivas.

2.  Es el conjunto de símbolos y reglas que se
utilizan para representar cantidades o datos
numéricos.
 A estos símbolos se los denomina cifras.
 Se caracterizan por la base a la que hacen
referencia, esta determina el número de
símbolos.
 Nosotros utilizamos el sistema de numeración
en base 10 (0, 1, 2, 3, 4, 5, 6, 7, 8, 9)

3. Sistemas de numeración
 Los principales sistemas de numeración son:

5. Sistemas de numeración

6. 0, 1, 2, 3, 4, 5, 6,
7

7. 0, 1, 2, 3, 4, 5, 6, 7,8,
9, A, B, C, D, E , F

8. EJERCICIOS:
 Señala los números que no pertenecen a sus
respectivos sistemas de numeración:
234
568(8)
101021(2)
3451(5)
456(8)

9. Teorema fundamental de la numeración (TFN)
Sirve para transformar de cualquier sistema de
numeración al sistema decimal (base 10)
254= 2.102+5.101+4.100
=200+50+4
= 254
283= 2.102+8.101+3.100
=200+80+3
= 283
Los sistemas de numeración que utilizamos
son sistemas posicionales y están basados en
el teorema fundamental de la numeración.

10. 254,125= 2.102+5.101+4.100+1.10-1+2.10-2+5.10-3
=200+50+4+0,1+0,02+0,005
= 254,125
254(8)= 2.82+5.81+4.80
=128+40+4
= 172
254(6)= 2.62+8.61+3.60
=72+48+3
= 123

11. Divisiones Sucesivas
 Sirven para convertir del sistema decimal a cualquier
otro sistema de numeración
BINARIO
125 OCTAL
DECIMAL HEXADECIMAL

12. Se divide el número del sistema decimal entre 2, cuyo resultado entero se
vuelve a dividir entre 2, y así sucesivamente hasta que el dividendo sea
menor que el divisor. Es decir, cuando el número a dividir sea 1 o 0 finaliza la
división.
A continuación se ordenan los restos empezando desde el último al primero,
obteniéndose el número binario correspondiente al número decimal
El número 26 en el sistema
Decimal al transformarlo al
sistema Binario sería 11010, ya
que como dijimos se debe leer a
partir de la última división
realizada

13. Se divide el número del sistema decimal entre 8, cuyo resultado
entero se vuelve a dividir entre 8, y así sucesivamente hasta que el
dividendo sea menor que el divisor. Es decir, cuando el número a
dividir se encuentre entre el 0 y el 7 finaliza la división.
A continuación se ordenan los restos empezando desde el último al
primero, obteniéndose el número octal correspondiente al número
decimal
El número 269 en el sistema
Decimal al transformarlo al
sistema Octal sería 415, ya que
como dijimos se debe leer a partir
de la última división realizada

14. Se divide el número del sistema decimal entre 16, cuyo resultado entero se
vuelve a dividir entre 16, y así sucesivamente hasta que el dividendo sea menor
que el divisor. Es decir, cuando el número a dividir se encuentre entre el 0 y el 15
finaliza la división.
A continuación se ordenan los restos empezando desde el último hasta al
primero, los números obtenidos entre el 10 y el 15 se reemplazan por la letra
correspondiente es decir 10=A, 11=B, así sucesivamente hasta 15=F,
obteniéndose el número correspondiente al número decimal.
El número 1869 en el sistema
Decimal al transformarlo al
sistema Hexadecimal sería 74D,
ya que como dijimos se debe leer
a partir de la última división
realizada

15. Decimal fraccionario a binario?
1. La parte entera se separa para poder
dividirla normalmente de decimal a
binario.
42,375

16. 2. La parte fraccionaria hacemos los siguientes pasos:
• Multiplicamos para 2
• Tomamos la parte entera que ira formando el numero
binario
• Tomamos la parte fraccionaria y seguimos multiplicando
para 2 y así sucesivamente hasta que llegue a 0 o hasta el
numero de dígitos solicitado.
42, 375
Parte
fraccionaria
Resultado de
la parte
fraccionaria

17.  El resultado será la unión de binario a la parte
entera y numero binario a la parte fraccionaria lo
unimos en un solo numero binario.