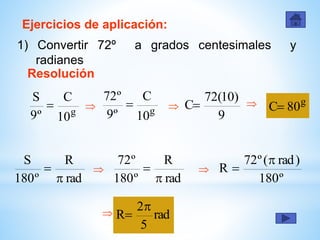
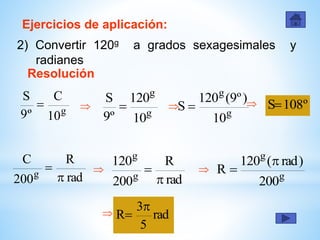
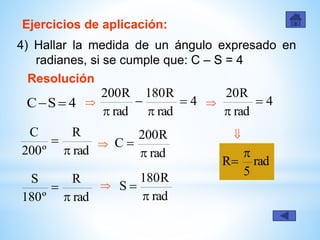
Este documento presenta información sobre diferentes sistemas de medida angular como el sistema sexagesimal, centesimal y radial. Explica las unidades, notaciones y equivalencias de cada sistema. Incluye ejemplos de conversión entre sistemas y ejercicios de aplicación para practicar conversiones.

1. ESCUELA DE POSGRADO
MAESTRÍA EN EDUCACIÓN
MENCIÓN:
GESTIÓN DE ENTORNOS VIRTUALES PARA EL APRENDIZAJE
UNIVERSIDAD CATÓLICA DE SANTA MARÍA
“PRESENTACIÓN EN POWER POINT”
CURSO: HERRAMIENTAS TECNOLOGICAS PARA LA IMPLEMENTACION DE ENTORNOS
VIRTUALES PARA EL APRENDIZAJE
Presentado por: Lic. Erick Bernardo Pelayo Baldárrago
BECA MAESTRO 3.0 - II ETAPA - GRUPO 7.
DOCENTE: Dr. VICTOR PALOMINO FLORES
AREQUIPA - PERÚ

2. SISTEMAS
DE MEDIDA
ANGULAR

3. SISTEMAS DE MEDIDA ANGULAR
1.- El sistema sexagesimal
2.- El sistema centesimal
3.- El sistema radial
6.- Ejercicios propuestos
4.- Relación entre sistemas
5.- Ejercicios de aplicación

4. SISTEMA SEXAGESIMAL
Sistema inglés.
Unidad de medida angular:
Grado sexagesimal (º).
Grado sexagesimal (º) es la
360ava parte de una
circunferencia.

5. SISTEMA SEXAGESIMAL
nciaCircunfere
360
1
O
A
B
1º
Notación:
1º: un grado sexagesimal
1’: un minuto sexagesimal
1’’: un segundo sexagesimal
Equivalencias:
Una vuelta   360º
1º   60’
1’   60’’
1º   3600’’

6. Ejercicios de aplicación :
1) Expresar 3945’ en grados sexagesimales
Resolución
Usando las equivalencias respectivas tenemos
º75,65





'60
º1
'3945

7. Ejercicios de aplicación:






''60
'1
''30
2) Expresar 45º25’30’’ a grados sexagesimales
Primero pasamos los 30’’ a minutos
'5,0
Ahora tenemos 45º25,5’






'60
º1
'5,25 º425,0
Sumamos: 45º + 0,425º
45,425º
45º25’30’’   45,425º

8. Ejercicios de aplicación :
3) Expresar 87,32º en grados, minutos y
segundos sexagesimales
Resolución






º1
'60
º32,0
87º + 0,32º
'2,19
87º + 19’ + 0,2’






'1
''60
'2,0 ''12
87º +19’ + 12’’ 87,32º  87º19’12’’

9. Ejercicios de aplicación :
4) Expresar 4058’’ en grados, minutos y segundos
sexagesimales
Resolución
4058’’ 4058’’  1º7’38’’60’’
6458 7’
38’’
67’ 60’
1º
7’

10. SISTEMA CENTESIMAL
Sistema francés
Grado centesimal, es la 400ava parte de la
circunferencia.
Unidad de medida angular:
Grado centesimal

11. SISTEMA CENTESIMAL
nciaCircunfere
400
1
Notación:
1g: un grado centesimal
1m :un minuto centesimal
1s :un segundo centesimal
Equivalencias:
Una vuelta   400g
1g   100m
1m   100s
1g   10000s
O
A
B
1g

12. Ejercicios de aplicación :
1) Expresar 50g 25m 45s a grados centesimales
Resolución








m
g
m
100
1
25
g
0045,0
Primero pasamos los 45s a grados centesimales








s
g
s
10000
1
45
g
25,0
La expresión 50g 25m 45s podemos escribirla
50g +25m +45s   50g +0,0045g +0,25g
50g +25m +45s   50,2545g

13. Ejercicios de aplicación
2) Expresar 20,3465g a grados , minutos y
segundo centesimales
Resolución








g
m
g
1
100
3465,0
La expresión 20,3465g se puede escribir así
m
65,34
La expresión 20,3465g podemos escribirla
20g +34m +65s   20g 34m 65s
20g + 0,3465g








m
s
m
1
100
65,0
s
65
mm
65,034 

14. SISTEMA RADIAL
Sistema internacional
El radián: que es el ángulo en el centro de
la circunferencia cuya longitud de arco es
igual a la longitud del radio de la
circunferencia.
Unidad de medida:
El radián(rad).

15. SISTEMA RADIAL
Equivalencias:
Una vuelta   2rad
1/2   /2 radO
A
B
r
r
r

16. RELACION ENTRE SISTEMAS DE
MEDIDAS ANGULARES
rad2
R
400
C
º360
S
g 

 rad
R
200
C
º180
S
g 


17. Ejercicios de aplicación:
1) Convertir 72º a grados centesimales y
radianes
Resolución
g
10
C
º9
S
 g
10
C
º9
º72
 
9
)10(72
C  g
80C
rad
R
º180
S


rad
R
º180
º72

 
º180
)rad(º72
R


 rad
5
2
R



18. Ejercicios de aplicación:
2) Convertir 120g a grados sexagesimales y
radianes
Resolución
g
10
C
º9
S

g
g
10
120
º9
S
 
g
g
10
)º9(120
S   º108S
rad
R
200
C
g 

rad
R
200
120
g
g

 
g
g
200
)rad(120
R


 rad
5
3
R



19. Ejercicios de aplicación:
Resolución
rad
R
º180
S


rad
rad
4
5
º180
S


 
rad
rad
4
5
º180
S 





 
 º225S
escentesimalylessexagesimagradosarad
4
5
Expresar)3

rad
R
º200
C


rad
rad
4
5
º200
C


 
rad
rad
4
5
º200
S 





 

g
250S

20. Ejercicios de aplicación:
4) Hallar la medida de un ángulo expresado en
radianes, si se cumple que: C – S = 4
Resolución
4SC  4
rad
R180
rad
R200




 

rad
5
R


rad
R
º200
C


rad
R200
C



rad
R180
S


rad
R
º180
S


4
rad
R20




21. Ejercicios propuestos:
1) Expresar el complemento de 30º en el Sistema
Circular.
a) rad
3

rad
6
 rad
4

rad
5

rad
8

c)b) d) e)
2) Determinar la medida de un ángulo en radianes
sabiendo que 2
8
CR
20
SR




a) rad
6

rad
8
 rad
4

rad
5

rad
10

c)b) d) e)
3) Los ángulos congruentes de un triangulo isósceles
son ( 8x – 3 ) º y ( 9x – 4 )g hallar la medida del
ángulo desigual expresado en radianes
a) rad
3

rad
5
2 rad
10

rad
5
4
rad
2

c)b) d) e)

22. Ejercicios propuestos:
4) Hallar la medida de un ángulo expresado en
radianes si se cumple que 3S – 2C = 14
a) rad
9

rad
10

rad
2

rad
5

rad
8

c)b) d) e)
5) Determinar la medida de un ángulo en radianes
sabiendo que
m
mg
1
11
'1
'1º1
E 
a) rad rad2 rad
4

rad5 rad
10

c)b) d) e)
6) Calcular el valor de
a) 160 171 162 163 174c)b) d) e)
20
2
CRSR5





23. Gracias.