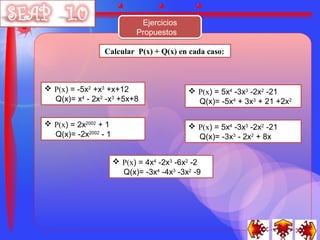
Este documento presenta un software educativo sobre adición de polinomios dirigido a estudiantes de segundo año de educación básica. Incluye definiciones, clasificaciones y ejemplos resueltos de polinomios, así como instrucciones y ejercicios propuestos sobre adición de polinomios.

1. Universidad de Carabobo
Facultad de Ciencias de la Educación
Dirección de Postgrado
Programa: Educación Matemática
Autores:
Licda. Katherine Lugo
Licda. Francis Cardozo
Julio de 2012

2. El siguiente material es un Software Educativo
dirigido a los estudiantes de 2do año de Educación
Básica y contiene contenidos referentes a la adición
de polinomios

3. Polinomios Ejercicios Resueltos
Adición de Ejercicios
Polinomios Propuestos
Actividades

4. Polinomios
Definición de Clasificación de los
Polinomio Polinomios
Elementos de un Orden de los
Polinomio Polinomios

5. Definición de
Polinomio
Un polinomio del griego, «poli»-muchos y «νόμος»-
división, y el latín «binomius») es
una expresión constituida por un conjunto finito
de variables (no determinadas o desconocidas)
y constantes (números fijos llamados coeficientes),
utilizando únicamente las operaciones aritméticas de
suma, resta y multiplicación, así como
exponentes enteros positivos. En otras palabras, es
una combinación lineal de productos de potencias
enteras de una o de varias indeterminadas.

6. Elementos de un
Polinomio
Un polinomio sobre Q de variable x tiene la forma: anxn+
an-1xn-1+… + a1x + a0 donde an, an-1… + a1, a0 son
números racionales que son llamados coeficientes del
polinomio.
Cada uno de los sumandos anxn , an-1xn-1… a1x , a0 se
llaman términos del polinomio.
El termino a0 se llama término constante, ya que
multiplica a x0 que es igual a uno.
El grado de un polinomio es el mayor exponente con el
que aparece la variable con coeficiente no nulo.

7. Clasificación de los
Polinomios
Algunos polinomios reciben un nombre especial según el
numero de términos no semejantes:
Monomios: Es el polinomio que esta formado por un
solo termino. Por ejemplo: 6x5; -x4; 15x3 son monomios.
 Binomio: Es un polinomio formado por dos términos.
Fíjate en los ejemplos: P(x)=10x4-x3; Q(x)x3 +1;
Trinomio: Es un polinomio formado por tres términos.
Por ejemplo: P(x)=8x4+x3+x2; Q(x)=6x5-x4+15x3
El polinomio cero o polinomio nulo Es aquel cuyos
coeficientes son todos iguales a 0. P(x)=0
El polinomio constante: Esta formado por un solo
término constante. Por ejemplo: P(x)= 10; Q(x)= -3

8. Orden de los
Polinomios
Ordenas un polinomio de forma decreciente significa
colocar los términos, según su grado, de mayor a menor.
Ejemplo: el polinomio 9x5 + 6x10 + 3 + 5x3 + 2x4 se escribe
en forma decreciente así: 6x10 + 9x5 + 2x4 + 5x3 + 3
Ordenar un polinomio en forma creciente significa
escribir los términos del polinomio, según su grado, de
menor a mayor. Ejemplo: 4x4 + 3x3 - x + 2x2 se escribe en
forma creciente así: - x + 2x2 + 3x3 + 4x4

9. Adición de
Polinomios
Para sumar polinomios los colocamos uno
debajo del otro, de forma en que los
términos semejantes queden en columnas;
luego se reducen los términos semejantes
obteniendo la suma.

10. Adición de
Polinomios
Pasos para la adición de polinomios
Se ordena el polinomio de forma decreciente o
creciente.
Se completa el polinomio.
Se ordenan los polinomios de igual grado, uno
debajo del otro.
Se efectúa una suma algebraica entre los
coeficientes.

11. Ejercicios Resueltos
Ejemplo N°1
Suma 2x2 + 6x + 5 y 3x2 - 2x - 1
Junta los términos similares: 2x2 + 3x2 + 6x - 2x + 5 - 1
Suma los términos similares: (2+3)x2 + (6-2)x + (3-1)
= 5x2 + 4x + 4
Ejemplo N°2
Suma: (2x2 + 6y + 3xy) + (3x2 - 5xy - x) + (6xy + 5)
Ponlos alineados en columnas y suma:
2x2 + 6y + 3xy
3x2 - 5xy - x
6xy +5
5x2 + 6y + 4xy - x + 5

12. Ejercicios Resueltos
Ejemplo N°3
Suma -4x3 + 7x2 + x + 5 y 9x2 - 5x - 10
Junta los términos similares: -4x3 + 7x2 + 9x2 + x - 5x + 5 - 10
Suma los términos similares: -4x3 + (7+9)x2 + (1-5)x + (5-10)
= -4x3 + 16x2 - 4x - 10
Ejemplo N°4
Suma: (5x3 - 12x2 + 3y + 5xy) + (6x3 + 8x2 - 3xy - x) + (6xy - 6)
Ponlos alineados en columnas y suma:
5x3 - 12x2 + 3y + 5xy
6x3 + 8x2 - 3xy - x
6xy + 5
11x3- 4x2 + 3y + 8xy - x + 5

13. Ejercicios Resueltos
Ejemplo N°5
HALLAR = A + B
A(x) = 0m4 + ½ m3 + 0m2 + 0m + 6
B(x) = 3m4 - ½ m3 + 0m2 -12m + 7
A+B = 3m4 +0/2 m3 +0m2 +12m + 13
4to ejemplo de
Suma
HALLAR = A + B
A(x) = -4m4 + 5 m3 + 10m2 + 8m - 7
B(x) = 2m4 - 6 m3 + 2m2 - 13m - 9
A+B = -2m4 - m3 + 12m2 - 5m - 16

14. Actividades
INSTRUCCIONES: Elige una alternativa de las que se te presentan,
luego pulsa la respuesta que consideres correcta y verás lo que
sucede …
¡Ahora suma,
juega
y diviértete!

15. ¿De que forma se
¿De que forma se
ordenan los
ordenan los
polinomios para la
polinomios para la
suma?
suma?
 En forma decreciente o creciente.
 En forma decreciente según los
coeficientes.
 En forma creciente.

16. M+N
M+N
M(x)=0p33+1/6p22+5p+0
M(x)=0p +1/6p +5p+0
N(x)=3p33+3/8p2+8p+16
N(x)=3p +3/8p2+8p+16
 0p6 + 4/14p4 + 13p + 0
 3p9 + 41/81p2 + 31p + 61
 3p3 + 51/18p2 + 13p + 16

17. P+Q
P+Q
P(x)=5x +3x33+2x22+x+21
44
P(x)=5x +3x +2x +x+21
Q(x)=0x44+3x33+2x22+8x+20
Q(x)=0x + 3x +2x +8x+20
 0x4+3x6 + 4x4 + 8x + 30
 5x4+6x3 + 4x2 + 9x + 41
 5x4+6x3 + 4x2 + 8x + 41

18. ¿Cuántos términos tiene el
¿Cuántos términos tiene el
siguiente polinomio:
siguiente polinomio:
P(x)=5x44+3x33+2x22+x+21
P(x)=5x +3x +2x +x+21
4
3
5

19. Es el polinomio que esta
Es el polinomio que esta
formado por un solo termino. Por
formado por un solo termino. Por
ejemplo: 6x55;-x44;15x33
ejemplo: 6x; -x; 15x
 Monomio.
 Binomio.
 Trinomio.

20. Ejercicios
Propuestos
Calcular P(x) + Q(x) en cada caso:
 P(x) = -5x2 +x3 +x+12  P(x) = 5x4 -3x3 -2x2 -21
Q(x)= x4 - 2x2 -x3 +5x+8 Q(x)= -5x4 + 3x3 + 21 +2x2
 P(x) = 2x2002 + 1  P(x) = 5x4 -3x3 -2x2 -21
Q(x)= -2x2002 - 1 Q(x)= -3x3 - 2x2 + 8x
 P(x) = 4x4 -2x3 -6x2 -2
Q(x)= -3x4 -4x3 -3x2 -9

21. Muy bien

22. Muy bien

23. Muy bien

24. Muy bien

25. Muy bien

31. "La matemática es la llave de
oro que abre todas las
ciencias"
Duruy