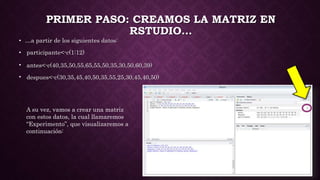
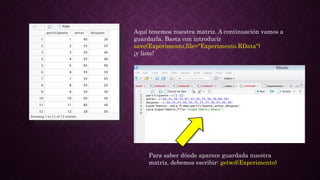
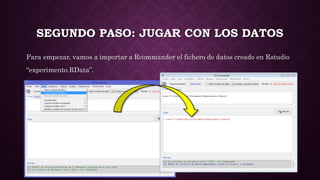
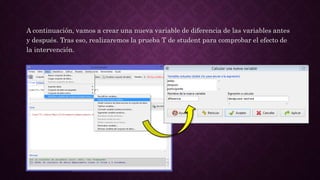
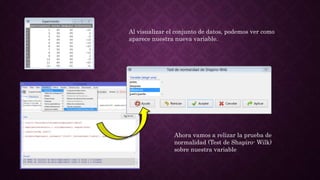
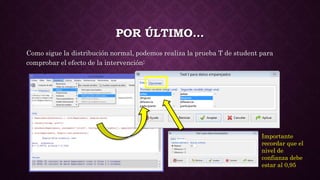
Este documento presenta los pasos para analizar los datos de un experimento antes y después de una intervención utilizando R. Primero, se crea una matriz con los datos de participantes, mediciones antes y después. Luego, se importan los datos a RCommander y se crea una nueva variable de diferencia. Se realizan pruebas de normalidad y T de Student, mostrando que hay una diferencia estadísticamente significativa entre antes y después. Finalmente, un boxplot ilustra el cambio entre ambas variables, corroborando que la intervención tuvo efecto.

1. EJERCICIO TEMA 11:
T DE STUDENT
Mariló Páyer Pérez
Macarena grupo 1
Subgrupo 3

2. PRIMER PASO: CREAMOS LA MATRIZ EN
RSTUDIO…
• …a partir de los siguientes datos:
• participante<-c(1:12)
• antes<-c(40,35,50,55,65,55,50,35,30,50,60,39)
• despues<-c(30,35,45,40,50,35,55,25,30,45,40,50)
A su vez, vamos a crear una matriz
con estos datos, la cual llamaremos
“Experimento”, que visualizaremos a
continuación:

3. Aquí tenemos nuestra matriz. A continuación vamos a
guardarla. Basta con introducir
save(Experimento,file="Experimento.RData")
¡y listo!
Para saber dónde aparece guardada nuestra
matriz, debemos escribir: getwd(Experimento)

4. SEGUNDO PASO: JUGAR CON LOS DATOS
Para empezar, vamos a importar a Rcommander el fichero de datos creado en Rstudio
“experimento.RData”.

5. A continuación, vamos a crear una nueva variable de diferencia de las variables antes
y después. Tras eso, realizaremos la prueba T de student para comprobar el efecto de
la intervención.

6. Al visualizar el conjunto de datos, podemos ver como
aparece nuestra nueva variable.
Ahora vamos a relizar la prueba de
normalidad (Test de Shapiro- Wilk)
sobre nuestra variable

7. ¿QUÉ NOS DICE EL TEST DE NORMALIDAD?
P-value tiene un valor de 0,7225. Como es mayor
que el error que asumimos ( 0,05) podemos
aceptar nuestra hipótesis nula y decir que sigue
una distribución normal.
RECORDEMOS QUE…
• Ho: La muestra se ajusta a la distribución normal (p>.05… se acepta la Ho)
• H1: La muestra NO se ajusta a la distribución normal (p≤.05)

8. POR ÚLTIMO…
Como sigue la distribución normal, podemos realiza la prueba T de student para
comprobar el efecto de la intervención:
Importante
recordar que el
nivel de
confianza debe
estar al 0,95

9. Como p valor es 0,03098 y hemos establecido un margen de error del
0,05, podemos afirmar que existe una diferencia estadísticamente
significativa.

10. BOXPLOT
Vamos a realizar un boxplot de ambas situaciones (antes y después) para compararlas

11. • Observando los boxplot, podemos afirmar que se ha producido un cambio entre
ambas variables, observando cómo, por ejemplo, la media ha disminuido casi 10
puntos.
• Para corroborar esta teoría, podemos ver el resumen numérico:
Con esto, afirmamos que la intervención ha producido efecto