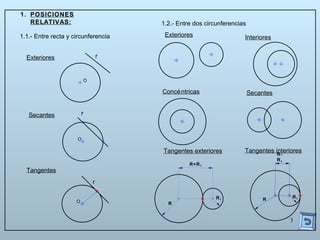
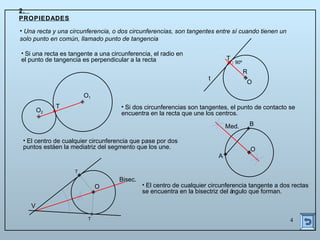
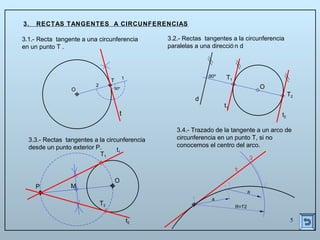
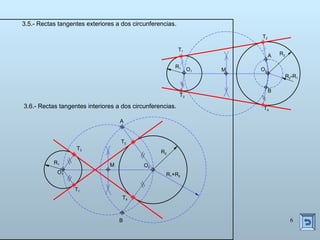
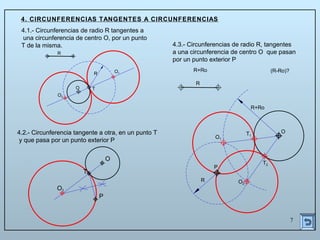
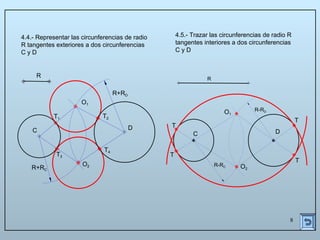
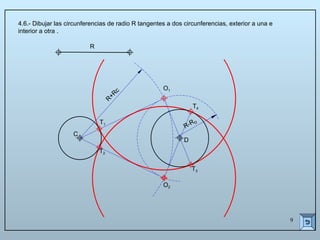
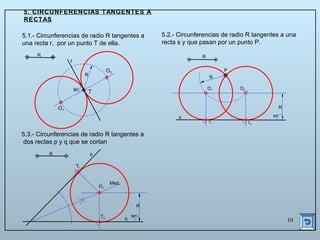
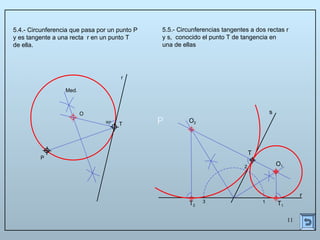
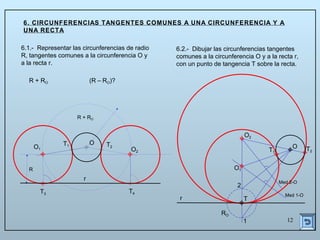
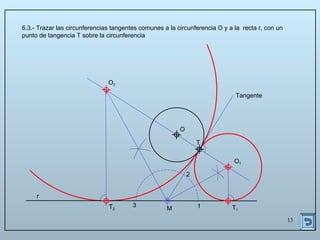
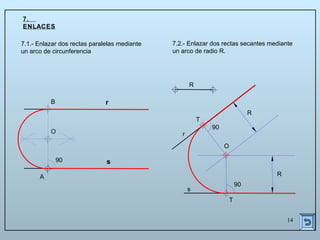
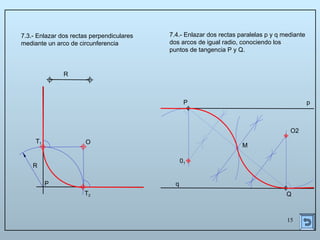
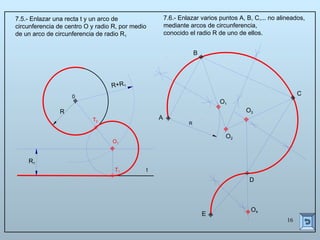
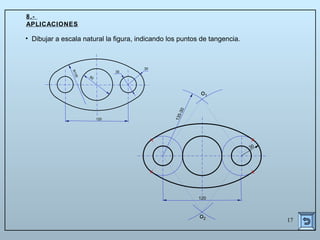
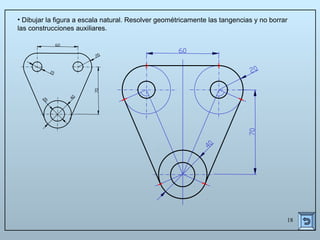
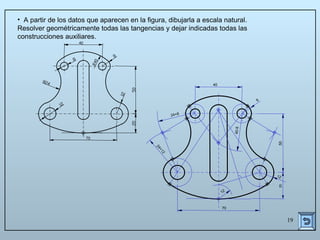
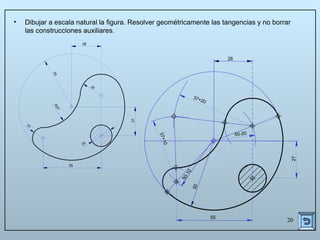
Este documento describe las propiedades y construcciones geométricas de las tangencias entre circunferencias y rectas. Explica cómo construir tangencias exteriores e interiores entre dos circunferencias o una circunferencia y una recta, así como cómo unir puntos o líneas mediante arcos de circunferencia tangentes. Finalmente, proporciona ejemplos prácticos de problemas geométricos que involucran tangencias.

1. 1Construcciones básicas
TANGENCIAS

2. 2
6.- Circunferencias tangentes comunes a una circunferencia y a una recta.
7.- Enlaces.
1.- Posiciones relativas.
CONTENIDO
2.- Propiedades.
3.- Rectas tangentes a circunferencias.
4.- Circunferencias tangentes a circunferencias.
5.- Circunferencias tangentes a rectas.
8.-
Aplicaciones

3. 3
InterioresExteriores
Tangentes interiores
SecantesConcéntricas
Tangentes exteriores
R
R1
R+R1
R
R1
R-
R1
1. POSICIONES
RELATIVAS:
1.1.- Entre recta y circunferencia
1.2.- Entre dos circunferencias
r
O
r
O
r
O
Exteriores
Secantes
Tangentes

4. 4
2.
PROPIEDADES
• Si una recta es tangente a una circunferencia, el radio en
el punto de tangencia es perpendicular a la recta
• Si dos circunferencias son tangentes, el punto de contacto se
encuentra en la recta que une los centros.
• El centro de cualquier circunferencia que pase por dos
puntos estáen la mediatriz del segmento que los une.
• El centro de cualquier circunferencia tangente a dos rectas
se encuentra en la bisectriz del ángulo que forman.
• Una recta y una circunferencia, o dos circunferencias, son tangentes entre sí cuando tienen un
solo punto en común, llamado punto de tangencia
R
90º
O
t
T
O1
O2
T
O
A
BMed.
Bisec.
O
V
T
T

5. 5
3. RECTAS TANGENTES A CIRCUNFERENCIAS
3.1.- Recta tangente a una circunferencia
en un punto T .
3.2.- Rectas tangentes a la circunferencia
paralelas a una direcció n d
3.3.- Rectas tangentes a la circunferencia
desde un punto exterior P.
3.4.- Trazado de la tangente a un arco de
circunferencia en un punto T, si no
conocemos el centro del arco.
t1
t2
T1
T2
d
O
O
P M
t1
t2
T1
T2
90º
a
a
R=T2
O
T 1
2
90º
t

6. 6
3.5.- Rectas tangentes exteriores a dos circunferencias.
3.6.- Rectas tangentes interiores a dos circunferencias.
A
B
T1
T3
T2
T4
MO1 O2
R1
R2
R2-R1
R1+R2
R2
O2
R1
O1
T2
T1
T3
T4
M
A
B

7. 7
4. CIRCUNFERENCIAS TANGENTES A CIRCUNFERENCIAS
4.1.- Circunferencias de radio R tangentes a
una circunferencia de centro O, por un punto
T de la misma.
R
O
R
T
O1
O2
4.3.- Circunferencias de radio R, tangentes
a una circunferencia de centro O que pasan
por un punto exterior P
P
O
R
R
R+Ro
T1
T2
O1
O2
4.2.- Circunferencia tangente a otra, en un punto T
y que pasa por un punto exterior P
O
T
P
O1
R+Ro (R-Ro)?

8. 8
R
C D
4.4.- Representar las circunferencias de radio
R tangentes exteriores a dos circunferencias
C y D
4.5.- Trazar las circunferencias de radio R
tangentes interiores a dos circunferencias
C y D
O1
O2
T
T
T
T
R-RD
R-RC
R+RC
R
C D
O1
O2
T1 T2
T3
T4
R+RD

9. 9
4.6.- Dibujar las circunferencias de radio R tangentes a dos circunferencias, exterior a una e
interior a otra .
R
C
D
R
+R
c
R-RD
O1
O2
T1
T3
T2
T4

10. 10
5. CIRCUNFERENCIAS TANGENTES A
RECTAS
5.1.- Circunferencias de radio R tangentes a
una recta r, por un punto T de ella.
5.2.- Circunferencias de radio R tangentes a una
recta s y que pasan por un punto P.
5.3.- Circunferencias de radio R tangentes a
dos rectas p y q que se cortan
R
s
P
R
R
90º
O1 O2
T1 T2
R p
q
O1
T1
T2
Med.
90º
R
O1
O2
r
T
R
R
90

11. 11
5.4.- Circunferencia que pasa por un punto P
y es tangente a una recta r en un punto T
de ella.
r
T
P
O
Med.
90º
5.5.- Circunferencias tangentes a dos rectas r
y s, conocido el punto T de tangencia en
una de ellas
T
s
r
T2 T1
O2
O1
1
2
3
P

12. 12
T2
6.1.- Representar las circunferencias de radio
R, tangentes comunes a la circunferencia O y
a la recta r.
6. CIRCUNFERENCIAS TANGENTES COMUNES A UNA CIRCUNFERENCIA Y A
UNA RECTA
6.2.- Dibujar las circunferencias tangentes
comunes a la circunferencia O y a la recta r,
con un punto de tangencia T sobre la recta.
R + RO (R – RO)?
R + RO
T4T3
T1 T2
R
O
r T
RO
1
2
Med 1-O
O1
T1
Med 2-O
O2
O
r
O1 O2

13. 13
6.3.- Trazar las circunferencias tangentes comunes a la circunferencia O y a la recta r, con un
punto de tangencia T sobre la circunferencia
O
r
T
Tangente
1
2
3
M
O1
T1
T2
O2

14. 14
R
r
s
7.
ENLACES
7.1.- Enlazar dos rectas paralelas mediante
un arco de circunferencia
7.2.- Enlazar dos rectas secantes mediante
un arco de radio R.
r
s
A
90
B
O
R
R
O
T
T
90
90

15. 15
R
P
7.3.- Enlazar dos rectas perpendiculares
mediante un arco de circunferencia
R
T1
T2
O
P
Q
p
q
7.4.- Enlazar dos rectas paralelas p y q mediante
dos arcos de igual radio, conociendo los
puntos de tangencia P y Q.
M
01
O2

16. 16
7.6.- Enlazar varios puntos A, B, C,... no alineados,
mediante arcos de circunferencia,
conocido el radio R de uno de ellos.
A
B
C
D
E
O1
O2
O3
O4
R
0
t
7.5.- Enlazar una recta t y un arco de
circunferencia de centro O y radio R, por medio
de un arco de circunferencia de radio R1
O1
T1
T2
R+R1
R
R1

17. 17
120
30
135-30
60
30
30
R135
120
o1
o2
• Dibujar a escala natural la figura, indicando los puntos de tangencia.
8.-
APLICACIONES

18. 18
• Dibujar la figura a escala natural. Resolver geométricamente las tangencias y no borrar
las construcciones auxiliares.

19. 19
24+8
24+12
40-8
12
12
8
70
50
40
20
• A partir de los datos que aparecen en la figura, dibujarla a escala natural.
Resolver geométricamente todas las tangencias y dejar indicadas todas las
construcciones auxiliares.

20. 20
50-20
50R37
10
20
27
28
55
20
28
37+20
37+10
50
55
27
50-10
• Dibujar a escala natural la figura. Resolver geométricamente las tangencias y no borrar
las construcciones auxiliares.