Este documento presenta dos ejercicios sobre probabilidad y distribuciones. El primer ejercicio calcula la probabilidad de que 60 o menos de 72 pruebas para detectar heroína en sangre estén correctamente evaluadas (1.15% de probabilidad), menos de 60 estén correctas (0.44% de probabilidad), y exactamente 60 estén correctas (0.71% de probabilidad). El segundo ejercicio analiza el nivel de glucosa en sangre de diabéticos, calculando la probabilidad de que sea inferior a 120 mg/100ml (50%), entre 90-130 mg/100

1. Función deFunción de
probabilidad yprobabilidad y
distribucióndistribución
TAREA 7

2. EJERCICIO 1EJERCICIO 1
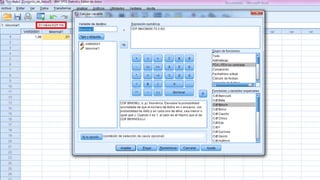
Una prueba de laboratorio para detectar heroína en sangre tiene un 92% de precisión. Si se analizan 72
muestras en un mes. Calcular las siguientes probabilidades:
a) 60 o menos estén correctamente evaluadas: P[60 o menos pruebas estén correctamente
evaluadas] = P[X ≤ 60]
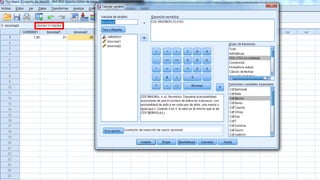
b) Menos de 60 estén correctamente evaluadas: P[menos de 60 pruebas estén correctamente
evaluadas] = P[X < 60] = P[X ≤ 59]
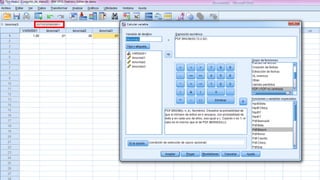
c) Exactamente 60 estén correctamente evaluadas: P[exactamente 60 estén correctamente
evaluadas] = P[X = 60]

3. a) 60 o menos estén correctamente evaluadas
1. Elegimos Transformar → Calcular variable
2. Nombraremos la nueva variable: binomial1
3. En grupo de funciones seleccionaremos FDA y FDA no centrada, en funciones Cdf.Binom
4. En la ecuación insertaremos los datos ( c=60, n=72, p=0.92)
EL RESULTADO SERÁ 1.15% DE PROBABILIDAD DE QUE 60 PRUEBAS O MENOSEL RESULTADO SERÁ 1.15% DE PROBABILIDAD DE QUE 60 PRUEBAS O MENOS
ESTÉN CORRECTAMENTE EVALUADASESTÉN CORRECTAMENTE EVALUADAS

5. b) Menos de 60 estén correctamente evaluadas
1. Elegimos Transformar → Calcular variable
2. Nombraremos la nueva variable: binomial2
3. En grupo de funciones seleccionaremos FDA y FDA no centrada, en funciones
Cdf.Binom
4. En la ecuación insertaremos los datos ( c=59, n=72, p=0.92)
EL RESULTADO SERÁ 0.44% DE PROBABILIDAD DE QUE 60 PRUEBAS O MENOSEL RESULTADO SERÁ 0.44% DE PROBABILIDAD DE QUE 60 PRUEBAS O MENOS
ESTÉN CORRECTAMENTE EVALUADASESTÉN CORRECTAMENTE EVALUADAS

7. c) Exactamente 60 estén correctamente evaluadas
1. Elegimos Transformar → Calcular variable
2. Nombraremos la nueva variable: binomial·
3. En grupo de funciones seleccionaremos FDP y FDP no centrada, en funciones
Pdf.Binom
4. En la ecuación insertaremos los datos ( c=60, n=72, p=0.92)
EL RESULTADO SERÁ 0.71% DE PROBABILIDAD DE QUE 60 PRUEBAS ESTÉNEL RESULTADO SERÁ 0.71% DE PROBABILIDAD DE QUE 60 PRUEBAS ESTÉN
CORRECTAMENTE EVALUADASCORRECTAMENTE EVALUADAS

9. EJERCICIO 2EJERCICIO 2
Se ha estudiado el nivel de glucosa en sangre en ayunas en un grupo de diabéticos. Esta variable se supone
que sigue una distribución Normal, con media 120 mg/100 ml y desviación típica 5 mg/100 ml. Se pide:
a) Obtener la probabilidad de que el nivel de glucosa en sangre en un diabético sea inferior a 120
mg/100 ml.
b) ¿Qué porcentaje de diabéticos tienen niveles de glucosa en sangre comprendidos entre 90 y 130
mg/100 ml?
c) Hallar el valor de la variable caracterizado por la propiedad de que el 25% y 50% de todos los
diabéticos tiene un nivel de glucosa en ayunas inferior a dicho valor.

10. a) Obtener la probabilidad de que el nivel de glucosa en sangre en un
diabético sea inferior a 120 mg/100 ml.
1. Elegimos Transformar → Calcular variable
2. Nombraremos la nueva variable: normal1
3. En grupo de funciones seleccionaremos FDA y FDA no centrada, en funciones
Cdf.Normal
4. En la ecuación insertaremos los datos ( c=120, media=120, desv_tip=5)
EL RESULTADO SERÁ 50% DE PROBABILIDAD DE QUE EL NIVEL DE UNEL RESULTADO SERÁ 50% DE PROBABILIDAD DE QUE EL NIVEL DE UN
DIABÉTICO SEA INFERIOR A 120mg/100mlDIABÉTICO SEA INFERIOR A 120mg/100ml

12. b) ¿Qué porcentaje de diabéticos tienen niveles de glucosa en sangre comprendidos entre 90 y
130 mg/100 ml?
1. Elegimos Transformar → Calcular variable
2. Nombraremos la nueva variable: normal2
3. En grupo de funciones seleccionaremos FDA y FDA no centrada, en funciones
Cdf.Normal
4. Realizaremos la resta de la frecuencia acumulada de 130 o menos – 89 o menos, ya que
el 90 está incluido
EL RESULTADO SERÁ 98% DE PROBABILIDAD DE QUE EL NIVEL DE UNEL RESULTADO SERÁ 98% DE PROBABILIDAD DE QUE EL NIVEL DE UN
DIABÉTICO ESTÉ COMPRENDIDO ENTRE 130mg/100ml y 90mg/100mlDIABÉTICO ESTÉ COMPRENDIDO ENTRE 130mg/100ml y 90mg/100ml

14. c) Hallar el valor de la variable caracterizado por la propiedad de que el 25% y 50% de todos los
diabéticos tiene un nivel de glucosa en ayunas inferior a dicho valor.
1. Elegimos Transformar → Calcular variable
2. Nombraremos la nueva variable: normal3 y normal4
3. En grupo de funciones seleccionaremos GL inversos, en funciones Idf.Normal
4. Realizaremos la operación para el percentil 25 y 50
EL RESULTADO SERÁ 116,3 mg/100ml PARA EL PERCENTIL 25 y 120 mg/100mlEL RESULTADO SERÁ 116,3 mg/100ml PARA EL PERCENTIL 25 y 120 mg/100ml
PARA EL PERCENTIL 50.PARA EL PERCENTIL 50.
LOS PACIENTES QUE SE HALLEN EN DICHOS PERCENTILES TENDRÁN ESALOS PACIENTES QUE SE HALLEN EN DICHOS PERCENTILES TENDRÁN ESA
GLUCOSAGLUCOSA