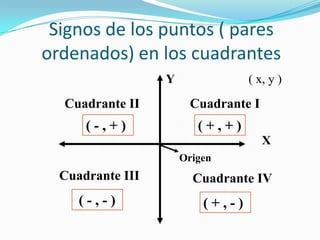
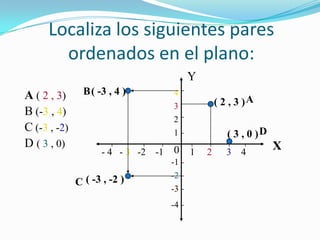
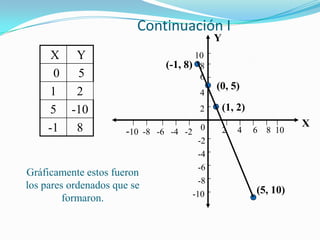
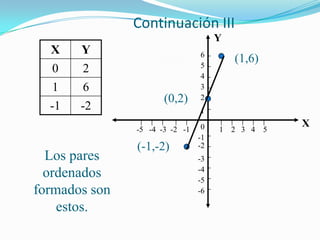
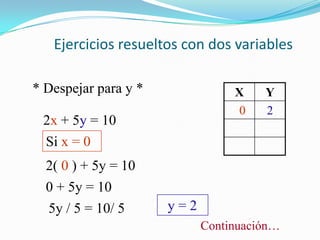
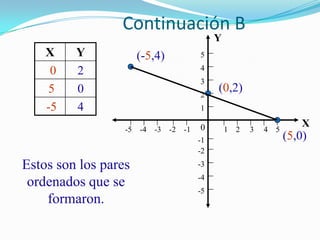
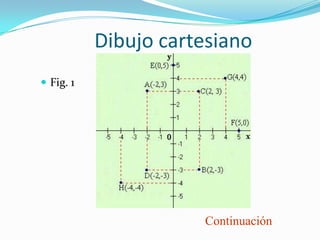
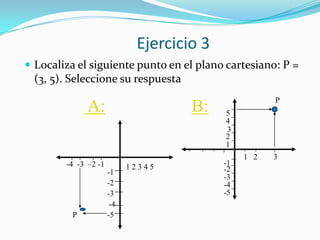
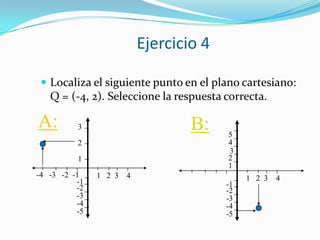
Este documento introduce la geometría analítica y el sistema de coordenadas cartesianas. Explica qué son las abscisas y ordenadas, cómo se definen los cuadrantes y pares ordenados, y cómo localizar puntos en el plano. Incluye ejemplos de ecuaciones y pares ordenados, así como una breve historia del desarrollo de este sistema por René Descartes.

1. Geometría Analítica
Tema 1.

2. Índice:
 Introducción
 Definición de Sistema de Coordenadas
 Definición de Par Ordenado
 Signos de los puntos en los cuadrantes
 Ejemplo de Par Ordenado
 Ejercicios resueltos
 Localizar pares ordenados en el plano
 Resuelve las ecuaciones
 Ejercicios resueltos con dos variables
 Un poco de historia no hace mal
 Ejercicios para practicar

3. Introducción
 Estas paginas han sido creadas con el objetivo de ayudar
al estudiante a entender mejor el funcionamiento y la
utilidad del Sistema de Coordenadas o Plano
Cartesiano. En la mismas encontrarás varios ejercicios
de practica, su explicación y procedimiento.
 Además podrá conectar a otras Páginas de Internet
relacionadas al tema.

4. Definición de Sistema de
Coordenadas
Es un sistema de ejes
coordenados, en que a cada punto
del plano le corresponde un par
ordenado de números reales, al
número del eje x se conoce como
abscisa, al eje Y ordenada.

5. Definición de abscisa
Abscisa: los números tomados
sobre el eje X que miden la
distancia en magnitud y el signo
desde el origen. El eje X se
llama, eje de las abscisas.

6. Definición de ordenada
Ordenadas: los números tomados
sobre el eje Y miden la distancia en
magnitud y signo desde el origen.
El eje Y recibe el nombre de
ordenada.

7. Coordenadas (x,y)
 Sabemos como se construye una recta
numérica. La línea horizontal es el eje de x, la
vertical es el eje de y y su intersección es el
origen. Estos ejes dividen el plano en cuatro
zonas llamadas cuadrantes.

8. Definición de Par Ordenado
Par de números de la forma ( x, y ) utilizados para
localizar puntos en un plano, se expresan en forma
de pares ordenados. El orden en que se escribe es
muy importante.

9. Signos de los puntos ( pares
ordenados) en los cuadrantes
Y ( x, y )
Cuadrante II Cuadrante I
(-,+) (+,+)
X
Origen
Cuadrante III Cuadrante IV
(-,-) (+,-)

10. Ejemplo de Par Ordenado
Ejemplo:
En el par ordenado ( 3 , 5) el 3
corresponde al número localizado en el eje
de ( x ) y el 5 corresponde al número
localizado en el eje de ( y ).

11. Ejercicios resueltos:
Y
Par Ordenado ( 3 , 5) (3,5)
5
4
3
0 2
1
X
1 2 3 4
Origen

12. Localiza los siguientes pares
ordenados en el plano:
Y
A ( 2 , 3) B ( -3 , 4 ) 4
3 ( 2 , 3 )A
B (-3 , 4)
2
C (-3 , -2) 1 ( 3 , 0 )D
D ( 3 , 0) X
- 4 - 3 -2 -1 0 1 2 3 4
-1
-2
C ( -3 , -2 )
-3
-4

13. Resuelve las ecuaciones y dibuja las
gráficas ( x, y )
Ejemplo # 1 y = - 3x + 5
Si x = 0 y = -3 (0) + 5 = 0 + 5 = 5 (0,5)
Si x = 1 y = -3 (1) + 5 = -3 + 5 = 2 ( 1 , 2 )
Si x = 5 y = -3 (5) + 5 = -15 + 5 = -10 ( 5, -10 )
Si x = -1 y = -3 (-1) + 5 = 3 + 5 = 8 ( -1, 8 )

14. Continuación I
Y
X Y 10
(-1, 8) 8
0 5 6
(0, 5)
1 2 4
5 -10 2 (1, 2)
-1 8 X
-10 -8 -6 -4 -2 0 2 4 6 8 10
-2
-4
-6
Gráficamente estos fueron
-8
los pares ordenados que se (5, 10)
formaron. -10

15. Continuación II
Ejercicio # 2 ( x, y ) y = 4x + 2
Si x = 0 y = 4 (0) + 2 = 0 + 2 = 2 (0,2)
Si x = 1 y = 4 (1) + 2 = 4 + 2 = 6 ( 1 , 6 )
Si x = -1 y = 4 (-1) + 2 = -4 + 2 = - 2 ( -1,-2 )
X Y
Variable 0 2 Variable
independiente 1 6 dependiente
-1 -2

16. Continuación III
Y
X Y 6
5
(1,6)
0 2
4
1 6 3
(0,2) 2
-1 -2 1
0 X
-5 -4 -3 -2 -1 1 2 3 4 5
-1
(-1,-2) -2
Los pares -3
-4
ordenados -5
formados son -6
estos.

17. Ejercicios resueltos con dos variables
* Despejar para y * X Y
0 2
2x + 5y = 10
Si x = 0
2( 0 ) + 5y = 10
0 + 5y = 10
5y / 5 = 10/ 5 y=2
Continuación…

18. * Despejar para y *
X Y
2x + 5y = 10 0 2
5 0
Si x = 5
2( 5 ) + 5y = 10
10 + 5y = 10 5y = 10 - 10
5y = 0
Continuación…

19. Continuación, ejercicio anterior
* Despejar para y * X Y
2x + 5y = 10 0 2
5 0
Si x = -5
-5 4
2( -5 ) + 5y = 10
-10 + 5y = 10 5y = 10 + 10
5y = 20
5y/5 = 20/5 y=4
Continuación…

20. Continuación B
Y
X Y (-5,4) 5
0 2 4
3
5 0 2
(0,2)
-5 4 1
0 X
-5 -4 -3 -2 -1 1 2 3 4 5
-1 (5,0)
-2
Estos son los pares -3
-4
ordenados que se
-5
formaron.

21. Un poco de historia no hace mal
 Las Coordenadas son grupos de números que
describen una posición: a lo largo de una línea, en
una superficie o en el espacio. La latitud y longitud
o la declinación y ascensión recta, son sistemas de
coordenadas en la superficie de una esfera: en el
globo de la Tierra o en el globo de los cielos.
Continuación

22. Continuación historia
 El sistema de coordenadas cartesianas
fue conocido con el nombre de René
Descartes ("De-kart"), un científico y
filósofo francés que, hacia el año
1600, ideó una forma sistemática de
designar cada punto en el plano por
medio de dos números.
Continuación

23. Continuación de historia
El sistema se basa en dos líneas
rectas ("ejes"), perpendiculares entre
sí, cada una marcada con las
distancias desde el punto donde se
juntan ("origen"). (vea el dibujo en
la próxima pagina).
Continuación

24. Dibujo cartesiano
 Fig. 1
Continuación

25. Continuación histórica
La distancia en un eje se llama "x"
y en el otro "y". Dado un punto P
se dibujan, desde él, líneas
paralelas a los ejes y los valores
de "x" e "y" definen totalmente el
punto. En honor a
Descartes, (figura 2) se conoce
como sistema cartesiano.

26.  René
Descartes

27. Practicar para no olvidar

28. Ejercicio 1
 ¿Cuales signos corresponden al primer cuadrante en
el plano cartesiano? Recuerda que se gira contrario a
la manecilla del reloj:
 A: ( + , - )
 B: ( + , + )

29. Ejercicio 2
 ¿Cuales signos corresponden al tercer cuadrante en el
plano cartesiano?:
 A: ( - , - )
 B: ( + , + )

30. Ejercicio 3
 Localiza el siguiente punto en el plano cartesiano: P =
(3, 5). Seleccione su respuesta
P
A: B: 5
4
3
2
1
1 2 3
-4 -3 –2 -1 12345 -1
-1 -2
-3
-2 -4
-3 -5
-4
P -5

31. Ejercicio 4
 Localiza el siguiente punto en el plano cartesiano:
Q = (-4, 2). Seleccione la respuesta correcta.
A: 3 B: 5
2 4
3
1 2
1
-4 -3 -2 -1 1 2 3 4 1 2 3 4
-1 -1
-2 -2
-3 -3
-4 -4
-5 -5

32. Ejercicio 5
 Localiza el siguiente punto en el plano cartesiano:
R = (-1, -3). . Seleccione la respuesta correcta.
A: B:
3 R
3
2
2
1
1
-4 -3 -2 -1 1 2 3 4
-1 -4 -3 -2 -1
-2 -1
-2
R -3 -3
-4 -4
-5

33. Ejercicio 6
 Resuelve la ecuación y = 2x + 5 cuando x = 1.
Selecciona la alternativa correcta:
A: B:
(1,7) (3,5)

34. Ejercicio 7
 Resuelve la ecuación y = 3x + 7 cuando x = 2.
Selecciona la alternativa correcta:
A B
( 3 , 10 ) ( 2 , 13 )

35. Ejercicio 8
 Resuelve la ecuación y = 2x + 5 cuando x = 4
 A: ( 5 , 10 )
 B: ( 4 , 13 )
 C: ( 13 , 4 )

36. Ejercicio 9
 Resuelve la ecuación y = 2x + 5 cuando x = 5
 A: ( 2 , 5 )
 B: ( 5 , 15)
 C: ( 4 , 10 )

37. Ejercicio 10
 Resuelve la ecuación y = 2x + 5 cuando x = 0
 A: ( 0 , 5 )
 B: ( 5 , 2 )
 C: ( 1 , 4)

38. Direcciones en Internet relacionadas al tema
 http://www.cut-the-knot.org/Curriculum/index.shtml
 http://jahumada.metro.inter.edu/mrsg1010/unidad3/u3s1t1.htm
 http://omega.ilce.edu.mx:3000/sites/telesec/prope/htmlb/sec_39.html
 http://www.nuevaalejandria.com/archivos-curriculares/
 http://www.kn.pacbell.com/wired/bluewebn/index.cfm
 http://www.shodor.org/interactivate/activities/graphit/
 http://www.salonhogar.com/