Funciones exponenciales

JUSTIFICACIÓN
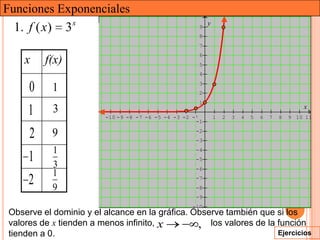
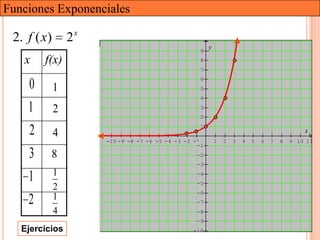
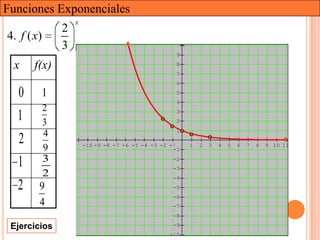
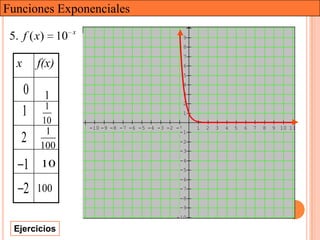
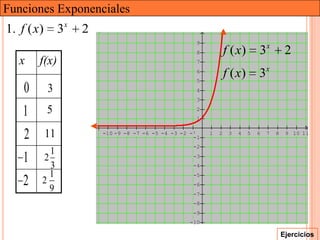
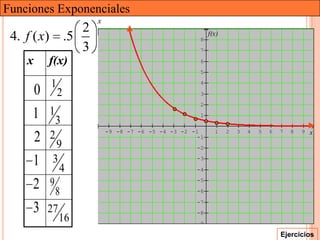
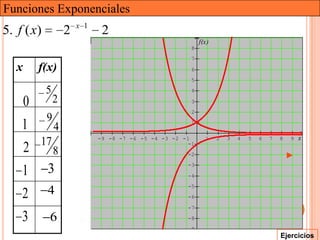
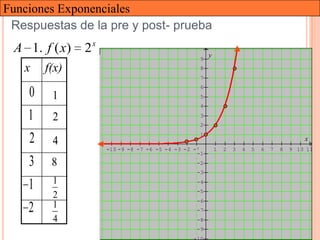
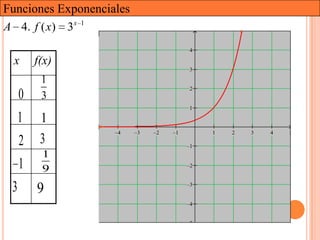
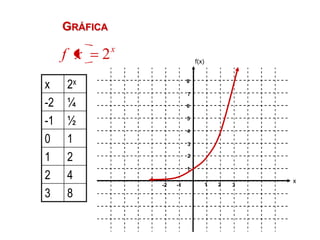
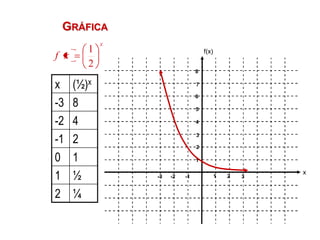
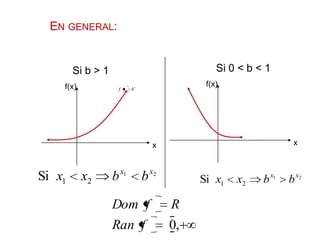
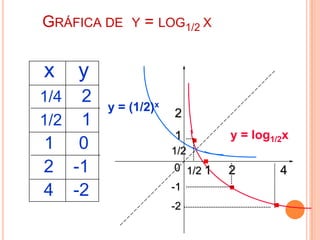
Las funciones exponenciales son
una de las familias
de funciones más importantes en
las matemáticas
por la gran cantidad de
aplicaciones que tienen..

Funciones Exponenciales
Pre-prueba
A. Traza la gráfica las B. Resuelve las siguientes
siguientes de funciones de ecuaciones exponenciales
exponenciales
1. f ( x ) 2 x
1. 23 x 6
2x 3

x
2. f ( x) 5
1
x 2. 34 x 2
3 x 4

3. f ( x )
3
3. 9x 3x 1
4. f ( x) 3x 1

5. f ( x ) e x

Definición de una función exponencial
•Sea b 0 y b 1 un número real. A una
función de la forma f ( x) b x
b.
•La x puede asumir cualquier valor real por lo que
el dominio de las funciones exponenciales es el
conjunto de los números reales, R , .
•Como la b 0 y b 1 los resultados al evaluar
las funciones exponenciales son números positivos
por lo tanto el alcance será, A 0, .
•Si b 1 la función será f ( x) 1 una función
constante, que no es exponencial.

“Estas funciones se conocen como funciones
exponenciales porque el exponente es variable.”

Ejemplos de funciones exponenciales
1. f ( x) 3x
2. f ( x) 4 x
x
2
3. f ( x)
3
4. f ( x) 5 x
x
5. f ( x) 10

Gráficas de funciones exponenciales

Ejemplos:
Traza la gráfica de las siguientes funciones
exponenciales.

1. f ( x) 3x Solución
2. f ( x) 2 x Solución
x
1
3. f ( x) Solución
2
x
2
4. f ( x) Solución
3
5. f ( x) 10 x Solución

1. f ( x) 3x 9
y
8
7
6
x f(x) 5
4
3
0 1 2
1
1 3 x
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 9 10 11
-1

2 9 -2
-3

1 -4
1 3
-5
-6
1
2 9
-7
-8
-9
-10
Observe el dominio y el alcance en la gráfica. Observe también que si los
valores de x tienden a menos infinito, x , los valores de la función
tienden a 0. Ejercicios

x
2. f ( x) 2
y
9
x f(x) 8
7
6
0 1 5
4

1 2 3
2
1
2 4 x
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 9 10 11
-1
3 8 -2
-3
1
1 -4
-5
2 -6
2 1 -7
4 -8
-9
Ejercicios -10

x
1
3. f ( x) y
2 9
8
x f(x) 7
6
5
0 1 4
3
1
1 2
2
1
x
1
2 4
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1
-1
1 2 3 4 5 6 7 8 9 10 11

-2

1 2 -3
-4
-5
2 4 -6
-7
-8
-9
Ejercicios -10

x
2
4. f ( x)
3
9

x f(x) 8
7
6

0 1 5
4
2 3
1 3 2
1
4
2 9 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 9 10 11
-1

1 3 -2
-3
2 -4
2 9 -5
-6
4 -7
-8

Ejercicios -9
-10

x
5. f ( x) 10 9
8
7
x f(x) 6
5
4
0 1 3
2
1
1 1
10
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 9 10 11
1 -1
2 100
-2
-3
-4
1 10 -5
-6

2 100 -7
-8
-9
-10

Ejercicios


Resumen de las propiedades de las funciones
exponenciales

1. Las funciones exponenciales pasan por el punto
(0,1).
2. Si b > 0 la función es creciente.
3. Si b < 0 la función es decreciente.
4. El eje de x es una asíntota horizontal.
5. El dominio es el conjunto de los números reales.
6. El alcance es el conjunto de números reales
positivos.
7. Las funciones exponenciales son uno a uno.


Transformaciones de las funciones exponenciales
Al igual que las funciones estudiadas anteriormente
podemos transformar las funciones exponenciales
variando sus parámetros (números) para producir
traslaciones, reflexiones, estiramientos y
contracciones. Las funciones que resultan de estas
transformaciones se conocen como funciones de
forma exponencial. Veremos algunos ejemplos a
continuación.


Transformaciones de las funciones exponenciales
Traza la gráfica de las siguientes funciones.
1. f ( x) 3x 2 Solución
x 1
2. f ( x) 2 Solución
x
1
3. f ( x) 2 Solución
2
x
2
4. f ( x) .5 Solución
3
x 1
5. f ( x) 2 2 Solución

6. f ( x) 2 x 2 Solución

1. f ( x) 3x 2
9
8 f ( x) 3x 2
x f(x) 7
6
5
f ( x) 3x
0 3 4
3

1 5 2
1

2 11 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1
-1
1 2 3 4 5 6 7 8 9 10 11

-2
1
1 2
3
-3
-4
1 -5
2 2
9 -6
-7
-8
-9
-10

Ejercicios

x 1
2. f ( x) 2 9
8
x f(x) 7
6
1 5

0 2
4
3
2
1 1 1

-10 -9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 9 10 11
2 2 -1
-2
-3
3 4 -4
-5
1
1 -6

4 -7

2 1 -8
-9
8 -10

Ejercicios

x
1
3. f ( x) 2 8
f(x)

2 7

x f(x) 6
5
4

0 2 3
2

1 1 1

-9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 9 x
-1
2 1 -2
2
-3

3 1
4
-4
-5
-6
1 4 -7
-8

2 8 -9

Ejercicios

x
2
4. f ( x) .5 8
8
f(x)
f(x)

3 7
7

x f(x) 6
6
5

1 4
0 2 3
2

1 1 1
3
-9 -8 -7 -6 -5 -4 -3 -2
-9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5
5 6
6 7
7 8
8 9
9 xx
2 2 -1
9 -2

1 3 -3

4 -4
-5
2 9
8 -6
-6
-7
-7
3 27 -8
-8
16 -9
-9

Ejercicios

x 1
5. f ( x) 2 2
f(x)
8
7
x f(x) 6
5

5 4

0 2 3
2
9
1 4
1

-9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 9 x
17 -1
2 8 -2
-3
1 3 -4
-5
2 4 -6

-7

3 6 -8
-9
Ejercicios

x 2
6. f ( x) 2
2 2 4 1 1
a. f ( 2) 2 2 x y
24 16 -2 1/16
1 2 3 1 1
b. f ( 1) 2 2 3 -1 1/8
2 8
0 1/4
2 1 1
c. f (0) 20 2
2 1 1/2
22 4
1 1 2 1
1 2 1
d . f (1) 2 2 1 3 2
2 2
2 2 0
e. f (2) 2 2 1
3 2
f . f (3) 2 21 2
Ejercicios

x 2
f ( x) 2 4

x y 3

-2 1/16 2

-1 1/8 1

0 1/4
-4 -3 -2 -1 1 2 3 4
1 1/2
-1
2 1
-2
3 2
-3
4 3
-4

Ejercicios

RESOLVER ECUACIONES EXPONENCIALES IGUALANDO LAS BASES.
LAS FUNCIONES EXPONENCIALES SON FUNCIONES UNO A UNO, POR
x y
LO TANTO a a SI Y SOLO SI X = Y .
ESTA PROPIEDAD NOS PERMITE RESOLVER ECUACIONES
EXPONENCIALES IGUALANDO LAS BASES. O SEA SI LAS BASES SON
IGUALES ENTONCES LOS EXPONENTES SON IGUALES.
Ejemplos:
Resuelve las siguientes ecuaciones.
3x 8 x 2 Solución
1. 2 2
4x 6 x
2. 3 3 Solución

x x 1
3. 27 3 Solución

4x 2
1
4. 2x 2 Solución
2
x
x 2 2
5. 16 Solución
64
6 x 10 x 1
2 3
6. Solución
3 2
x 2
4x 2 1 Solución
7. e
e
x2 2 x x2 5 Solución
8. 4 2

3x 8 x 2
1. 2 2 Verificación
33 8 3 2
3x 8 x 2 2 2
9 8 1
3x x 2 8
2 2

2x 6 2 2
x 3
C.S 3

Ejercicios

4x 6 x
6 6
4 6
4x 6 x 3 5
3 5

4x x 6 24 30 6
5 5 5
3 3
5x 6
6 6
6 3 5
3 5
x
5
6
C.S
5
Ejercicios

x x 1
1 1
3 x x 1 1
3 3 27 2
3 2

1 3
3x x 1 3 2 2
3 3
2x 1 3 3
2 2
1 3 3
x
2

1
C.S
2
Ejercicios

4x 2
1 x 2
4. 2
2
1 4x 2 x 2
2 2
4x 2 x 2
2 2
4x 2 x 2
5x 4
4
4 C.S
x 5
5
Ejercicios

x
x2 2
5. 16
64
4 x2 5 x
2 2
5
2
C.S. = 0,
4x 5x 4

4 x2 5x 0
x 4x 5 0
x 0 4x 5 0
5
x
4 Ejercicios


6 x 10 x 1
2 3
6. 7x 11
3 2
x 1 11
6 x 10 1 x
2 2 7
3 3
11
C.S.=
6x 10 x 1 7

6x x 1 10

Ejercicios

x 2
4x 2 1
7. e
e
4x 2 x 2
4x 2 x 2
4x 2 x 2
4x 2 x 2
4x x 2 2
4x x 2 2
3x 0
5x 4
x 0 4
x
4 5
C.S.= 0,
5
Ejercicios

x2 2 x x2 5
8. 4 2
2 x2 2 x x2 5
2 2
2 2
2x 4x x 5
2 2
2x x 4x 5 0
2
x 4x 5 0
x 5 x 1 0
x 5 0 x 1 0 C.S. 5, 1
x 5 x 1
Ejercicios

Funciones ExponencialesLAS FUNCIONES EXPONENCIALES
APLICACIONES DE
LAS FUNCIONES EXPONENCIALES TIENEN MUCHAS
APLICACIONES EN CIENCIAS, MATEMÁTICAS, COMERCIO Y
EN OTRAS DISCIPLINAS. VEREMOS AQUÍ ALGUNAS DE
ESAS APLICACIONES.

1. Fórmula de interés compuesto
r nt
A P 1
m
A es la cantidad acumulada o valor futuro
P es el principal de la inversión
r es la tasa de interés anual
n es el número de periódos de tiempo por año
t es el número años

2. Fórmula de interés continuo
A Pe it
A es la cantidad acumulada o valor futuro
P es el principal de la inversión
i es el interés anual
t es el número de años de la inversión

3. Fórmula de crecimiento y decaimiento exponencial
A t A0e kt
A es la cantidad acumulada luego de un tiempo t
A0 es la cantidad inicial
k es la constante de crecimiento o decaimiento,
t es el tiempo
Si k 0 hay crecimiento o aumento en el valor de A,
si k 0 elvalor de A decae o decrece.

4. Fórmula de enfriamiento de Newton
u t T u0 T e kt , k 0

u es la temperatura del objeto en un tiempo t
T es la temperatura del medioambiente
u0 es la temperatura inicial del objeto
t es el tiempo
k es una constante negativa

5. Fórmula de crecimiento logístico
c
P t
1 ae bt
P es la población en un tiempo t
a , b, c son constantes, c 0, b 0
t es el tiempo en años
c es la capacidad de crecimiento pues lim P t c
t

Resuelve el ejercicio.
1) Una muestra de 700 gramos de plomo 210 decae a polonio 210 de acuerdo a la
siguiente función, A(t) = 700e-0.032t, donde t es el tiempo en años. Encuentra la
cantidad de plomo 210 en la muestra luego de 60 años. (redondea a gramos)
A) 103g B) 64g C) 4775g D) 75g

2) Una muestra de 900 gramos de plomo 210 decae a polonio 210 de acuerdo a la
siguiente función, A(t) = 900e-0.032t, donde t es el tiempo en años. Encuentra la
cantidad de plomo 210 en la muestra luego de 100 años. (redondea a gramos)
A) 37g B) 56g C) 22,079 g D) 27g

3) Desde 1950, el crecimiento de la población mundial en millones de personas puede
ser aproximada por la función exponencial A(t) = 2600e0.018t, donde t es el número de
años desde 1950. Estima la población en el año 2003 al millón más cercano.
A) 6,629 millones B) 6,872 millones
C) 6,750 millones D) 36,152,864 millones

4) Desde 1950, el crecimiento de la población mundial en millones de personas puede
ser aproximada por la función exponencial A(t) = 2600e0.018t, donde t es el número de
años desde 1950. Estima la población en el año 2015 al millón más cercano.
A) 8,228 millones B) 8,529 millones C) 8,377 millones D) 313,486,458 millones

Encuentra el valor futuro de un principal P invertido durante m años a una tasa
de interés nominal anual r y compuesto como se indica. Redondea a dos lugares
decimales.
5) P = $1,000, m = 10, r = 7% compuesto anual
A) $1,967.15 B) $1,838.46 C) $2,104.85 D) $967.15

6) P = $1,000, m = 4, r = 9% compuesto semianual
A) $422.1 B) $1,411.58 C) $1,360.86 D) $1,422.10

7) P = $480, m = 2, r = 17% compuesto trimestralmente
A) $189.65 B) $642.35 C) $669.65 D) $657.07

8) P = $12,000, m = 8, r = 8% compuesto trimestralmente
A) $22,171.07 B) $22,211.16 C) $10,614.49 D) $22,614.49

Encuentra el valor presente de una cantidad A compuesto a una tasa de interés r por t
años. Redondea a centavos.
9) A = $5,600, t = 3, r = 8% compuesto anual
A) $7,938.32 B) $1,154.54 C) $4,445.46 D) $4,801.10

10) A = $10,500, t = 3, r = 4% compuesto semianual
A) $8,889.96 B) $9,707.84 C) $1,165.54 D) $9,334.46

11) A = $6,500, t = 8, r = 13% compuesto trimestral
A) $2,445.04 B) $2,411.69 C) $2,335.78 D) $4,164.22

12) A = $10,000, t = 4, r = 18% compuesto mensual
A) $4,893.62 B) $2,500.00 C) $8,363.87 D) $11,956.18

Resuelve el ejercicio.
13) La media vida del silicón-32 es 710 años. Si tenemos una muestra de 30 gramos. ¿Qué
cantidad habrá luego 300 años?
A) 22.383 B) 0 C) 29.134 D) 1.604

14) La media vida del silicón-32 es 710 años. Si tenemos una muestra de 40 gramos. ¿ Qué
cantidad habrá luego 300 años?
A) 29.845 B)0 C) 38.845 D)2.138

15) Un tronco fosilizado contiene un 28% de la cantidad normal de
carbono-14. ¿ Qué edad en años tiene el fósil? Use 5600 años como la media vida del
carbono 14.
A) 26,873 B)2649 C) 34,489 D) 10,266

carbono- 14. ¿ Qué edad en años tiene el fósil? Use 5600 años como la media vida del
carbono-14.
A) 27,429 B)2876 C) 34,262 D)9709

carbono-14. ¿ Qué edad en años tiene el fósil? Use 5600 años como la media vida del
carbono 14.
A) 20,685 B) 1123 C) 36,015 D) 16,453

18) Un termómetro con una lectura de 11 C se ubica en un salón con una temperatura
constante de 20 C. Si el termómetro tiene una lectura de 17 C luego de 6 minutos,
encuentra la lectura del termómetro luego de estar en el salón durante 10 minutos.
A) 7.91 C B) 18.56 C C) 21.44 C D) 20 C

19) Un termómetro con una lectura de 13 C se ubica en un salón con una temperatura
constante de 20 C. Si el termómetro tiene una lectura de 18 C luego de 6 minutos,
encuentra la lectura del termómetro luego de estar en el salón durante 9 minutos.
A) 11.350C B) 18.93 C C) 21.07 C D) 20 C

20) Un carnicero guarda una carne cuya temperatura es de 98 F colocándola en una
nevera con una temperatura constante de 35 F. Si la temperatura de la carne bajó a 91 F
en 5 minutos, ¿ Cuánto tiempo le tomará a la carne alcanzar una temperatura de 52 F?
Ley de enfriamiento de Newton:
U = T + (U0 – T)ekt : T = Ta + (T0 - Ta)ekt.
A) 18 minutos B) 56 minutos C) 3 minutos D) 16 minutos

930
21) La ecuación de crecimiento logístico P(t) =
1 30e 0.348t
modela la población de cierto tipo de bacterias en un plato de cultivo luego de t horas.
¿Cuánto tardará en que el número de bacterias sea de 620?
A) 2.86 horas B) 11.77 horas C) 8.61 horas D) 6.02 horas

240
22) La ecuación de crecimiento logístico P(t) =
1 59e 0.189t
representa la población de una especie introducida en un nuevo territorio luego de t
años. Encuentra la población luego de 20 años de introducida la especie.
A) 178 B) 102 C) 240 D) 113

Resuelve el ejercicio. Redondea a tres lugares.

23) Encuentra la tasa de interés anual que se requiere para duplicar una
inversión en 4 años.
A) 18.921% B) 17.329% C)9.46% D)31.607%

24) Encuentra el tiempo que se requiere para duplicar una inversión si la tasa de
interés es de 5.25% compuesto continuo.
A) 14.114 años B) 20.926 años C) 6.601 años D) 13.203 años

25) Encuentra el tiempo que se requiere para triplicar una inversión si la tasa de
interés es de 7.25% compuesto continuo.
A) 16.362 años B) 9.561 años C)7.577años D) 15.153 años


Post-prueba
B. Resuelve las siguientes
A. Traza la gráfica las
de ecuaciones exponenciales
siguientes de funciones
exponenciales 1. 23 x 6
2x 3

1. f ( x ) 2 x 4x 2 x 4
2. f ( x) 5 x 2. 3 3
x
1 x x 1
3. f ( x ) 3. 9 3
3
x 1
4. f ( x) 3
5. f ( x ) e x

Respuestas de la pre y post- prueba
x
A 1. f ( x) 2 y
9
x f(x) 8
7
6
0 1 5
4

1 2 3
2
1
2 4 x
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 9 10 11
-1
3 8 -2
-3
1
1 -4
-5
2 -6
2 1 -7
4 -8
-9

A 2. f ( x) 5 x
y

x f(x)

0 1

1 5 x

2 25
1
1 5
1
2
25

x
1
A 3. f ( x)
3
y

x f(x)

0 1
1
1 3
1
2 9
x

1 3
2 9

A 4. f ( x) 3x 1

x f(x)
1
0 3

1 1
2 3
1
1 9
3 9

A 5. f ( x) e x , e 2.71
y

x f(x)

0 1

1 e
x
2
2 e
1
1 e
1
2 2
e


3
B 1. 2 3x 6
2 x 3 x
2

2
B 2. 3 4x 2
3 x 4 x
5

x x 1
B 3. 9 3 x 1

DEFINICIÓN
La función f definida por:
f x bx , b 0 y b 1
Se llama función exponencial con base b.

GRÁFICA
x
f x 2 f(x)

x 2x 8

7

-2 ¼ 6

-1 ½ 5

4
0 1 3

1 2 2

1
2 4 x
-2 -1 1 2 3

3 8

GRÁFICA
x
1 f(x)
f x
2
8

x (½)x 7

6
-3 8 5

-2 4 4

-1 2 3

2

0 1 1

1 ½ -3 -2 -1 1 2 3
x

2 ¼

EN GENERAL:

Si b > 1 Si 0 < b < 1
f(x) f(x)
f x bx

x x

x1 x2
Si x1 x2 b b Si x1 x2 b x1 b x2

Dom f R
Ran f 0,

FUNCIÓN EXPONENCIAL NATURAL:

Es la función exponencial cuya base es igual a
“e”, donde e = 2.71828… f(x)
8

x ex 7

-2 0.14 6

5
-1 0.37 4

0 1 3

2
1 2.72 1

2 7.39 -2 -1 1 2 3
x

3 20.01

Función Logarítmica: Introducción
PREGUNTA DE REFLEXIÓN

 ¿A qué exponente debe elevarse 10 para
producir los números:
a. 1000 ?
b. 0,001 ?
c. -1000 ?
d. 50 ?

LOGARITMO COMÚN (EN BASE 10)

y = log x significa 10y = x

Ejemplos:
log 1= 0, Porque 100=1
log 0,01 = -2, Porque 10-2=0,01
log 10 = ½ , Porque 101/2 = 10

LOGARITMO NATURAL COMÚN (BASE E)

y = ln x significa ey = x
Ejemplos:
ln 1= 0, Porque e0=1
ln 10 = 2,3025… Porque e2,3025…=10
ln ek = k , Porque ek = k

LOGARITMO EN BASE “A”

y = loga x significa ay = x

 donde a: base
y: exponente

FORMA
EXPONENCIAL LOGARÍTMICA

•32 = 9 •log3 9 = 2
•4-3 = 1/64 •log4 (1/64) = -3
•(1/5)-2 = 25 •log1/5 25 = -2
•103 = 1000 •log 1000 = 3
•e0 = 1 •ln 1 = 0

FUNCIÓN LOGARITMO
La función logaritmo de base a, donde a>0y
a 1, se define como:

f(x) = logax

Observación:
1. Si x1 x2 , entonces loga x1 loga x2
2. Si loga x1= loga x2, entonces x1= x2

GRÁFICAS DE Y = 2X, Y = LOG2 X

x y y = 2x

1/4 -2
1/2 -1
2
1 . . y = log 2x
1 0 1/2
.
2
4
1
2
-1 .
0 1/2 1 2 4

-2

GRÁFICAS DE Y = EX, Y = LNX
y

y

x

x

GRÁFICA DE Y = LOG1/2 X

x y
1/4 2
y = (1/2)x 2
1/2 1
1 . y = log1/2x
1
2
0
-1
1/2
.
4 -2
0 1/2 1
-1 . .
2 4

-2

GRÁFICA DE Y = LOGAX PARA A >1

y = bx De la gráfica:
loga1 = 0
b
logaa = 1
1 y = log bx
loga0 no definido
1 b logax < 0 si x<1
logax > 0 si x>1
Es creciente

FUNCIÓN EXPONENCIAL
1. Graficar: y = e-x
2. Graficar: y = ex+2
3. Graficar: y = ex + 3

4. La población proyectada P de una ciudad
0.05t
está dada por: P 100,000e
Donde t es el número de años después
de 1990. Pronosticar la población para el
año 2010.

FUNCIÓN LOGARÍTMICA
Graficar las siguientes funciones, indicando su
dominio y rango:
1. y = ln(x-3)
2. y = ln(-x)
3. y = ln(x+1) – 2
4. y = -ln(x+3) + 1

Funciones exponenciales

Más contenido relacionado

La actualidad más candente

Similar a Funciones exponenciales

Más de Carlos Calle

Funciones exponenciales