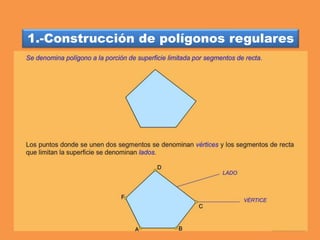
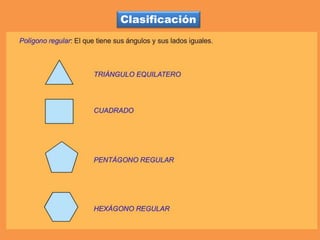
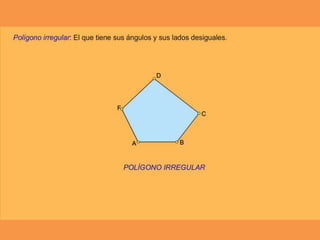
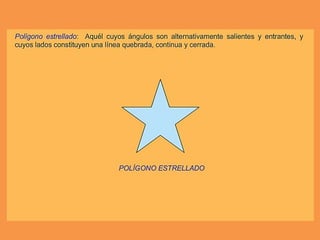
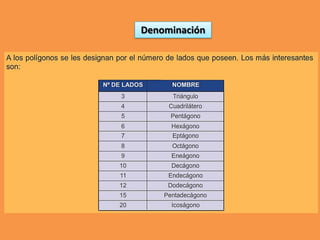
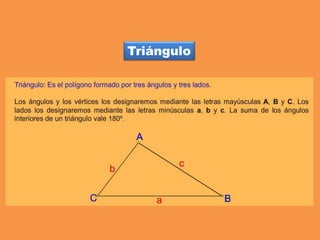
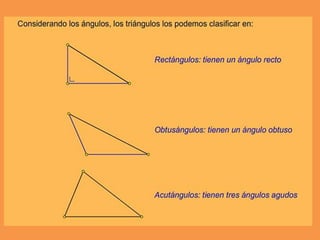
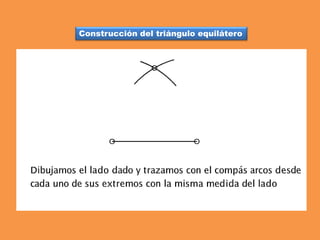
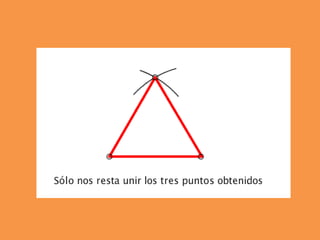
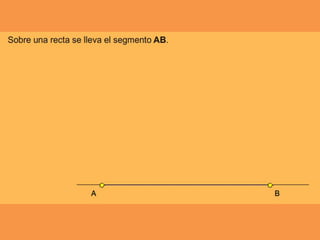
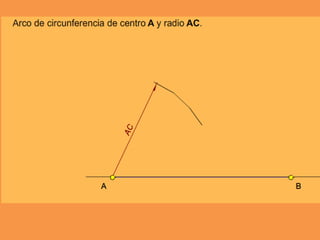
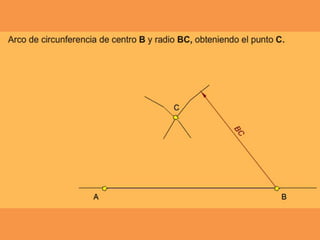
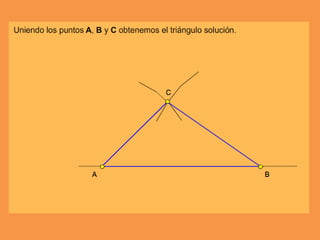
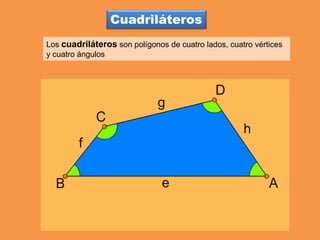
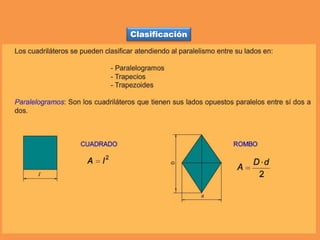
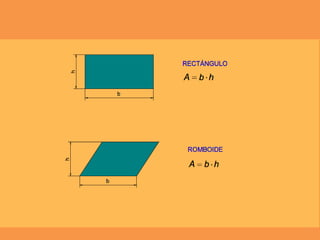
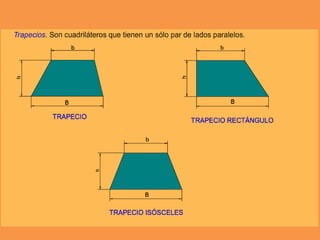
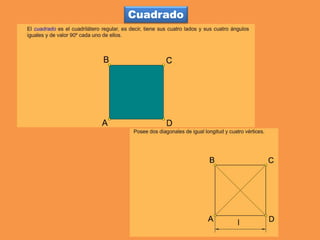
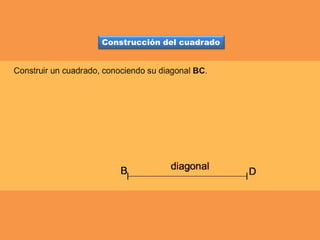
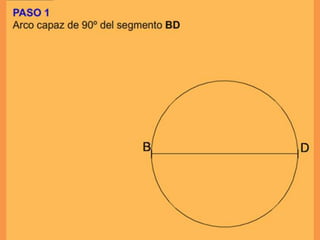
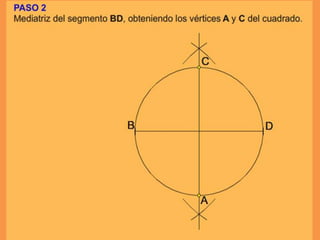
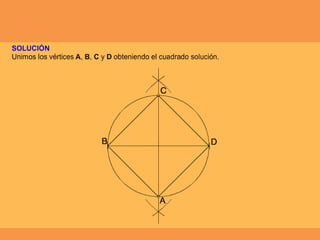
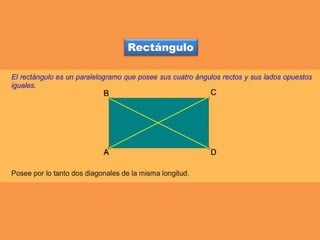
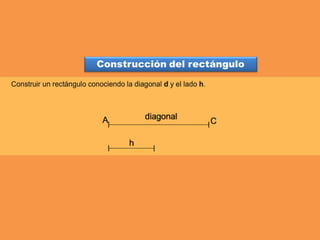
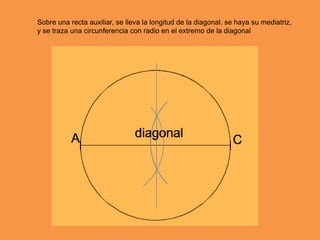
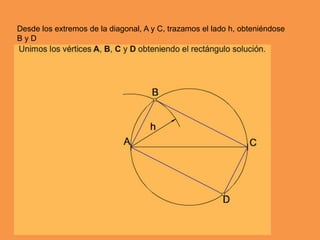
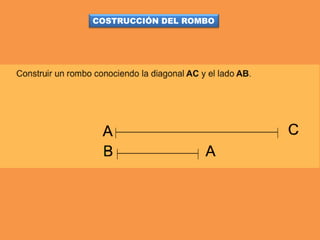
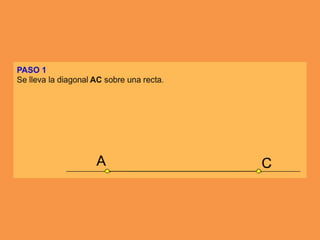
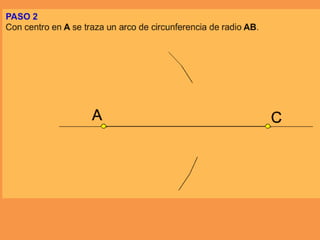
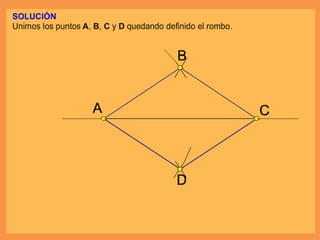
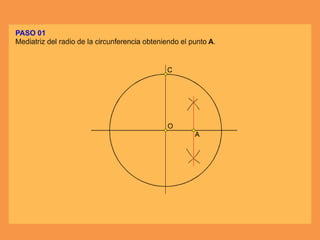
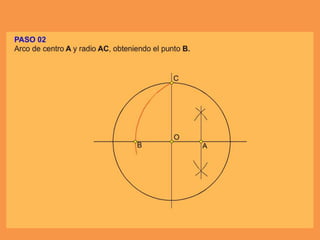
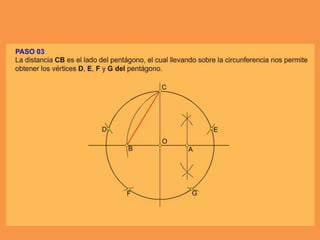
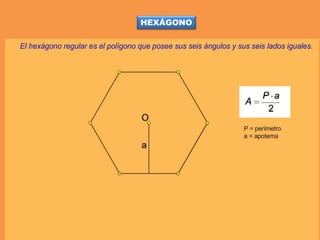
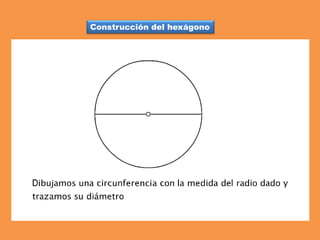
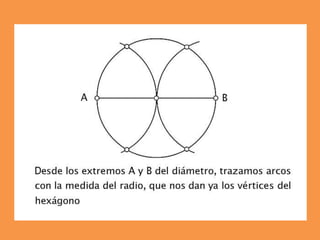
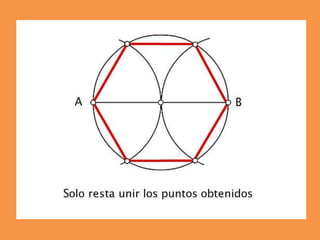
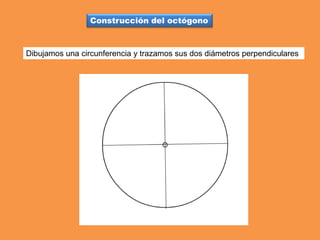
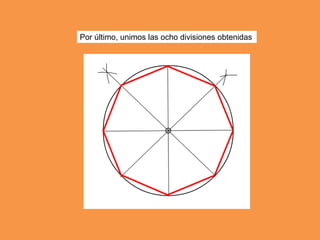
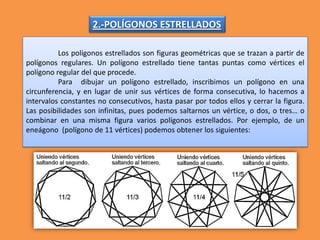
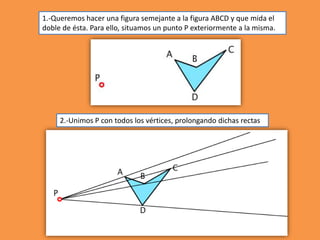
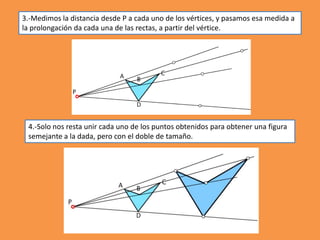
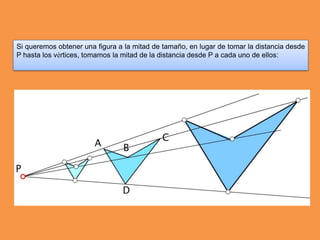
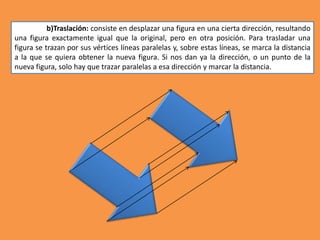
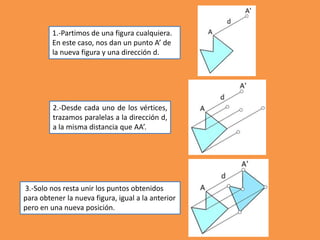
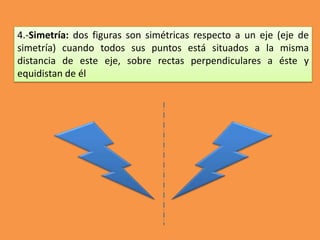
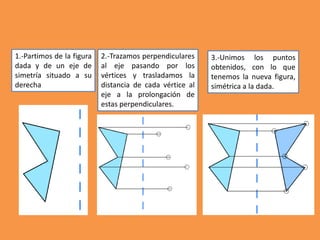
Este documento presenta los conceptos básicos de trazados geométricos en dibujo técnico para segundo año de ESO. Explica cómo construir polígonos regulares como triángulos, cuadrados y hexágonos, y describe polígonos estrellados y transformaciones geométricas como semejanza, traslación y simetría.

1. DIBUJO TÉCNICO 2º ESO
TEMA 1.- TRAZADOS BÁSICOS
IES. FUENTE NUEVA

2. 1.-Construcción de polígonos regulares

3. Clasificación

6. Denominación

7. Triángulo

10. Construcción del triángulo equilátero

12. Construcción del triángulo escaleno

17. Los cuadriláteros son polígonos de cuatro lados, cuatro vértices
y cuatro ángulos
Cuadriláteros

18. Clasificación

22. Cuadrado

23. Construcción del cuadrado

27. Rectángulo

29. Sobre una recta auxiliar, se lleva la longitud de la diagonal. se haya su mediatriz,
y se traza una circunferencia con radio en el extremo de la diagonal

30. Desde los extremos de la diagonal, A y C, trazamos el lado h, obteniéndose
B y D

31. Rombo

32. COSTRUCCIÓN DEL ROMBO

37. PENTÁGONO

43. HEXÁGONO

44. Construcción del hexágono

47. Construcción del octógono
Dibujamos una circunferencia y trazamos sus dos diámetros perpendiculares

48. Trazamos las bisectrices de dos de los cuatro ángulos,
que prolongamos hacia el ángulo opuesto

49. Por último, unimos las ocho divisiones obtenidas

50. 2.-POLÍGONOS ESTRELLADOS
Los polígonos estrellados son figuras geométricas que se trazan a partir de
polígonos regulares. Un polígono estrellado tiene tantas puntas como vértices el
polígono regular del que procede.
Para dibujar un polígono estrellado, inscribimos un polígono en una
circunferencia, y en lugar de unir sus vértices de forma consecutiva, lo hacemos a
intervalos constantes no consecutivos, hasta pasar por todos ellos y cerrar la figura.
Las posibilidades son infinitas, pues podemos saltarnos un vértice, o dos, o tres… o
combinar en una misma figura varios polígonos estrellados. Por ejemplo, de un
eneágono (polígono de 11 vértices) podemos obtener los siguientes:

51. A partir de los polígonos estrellados se pueden obtener
diferentes y muy ricas composiciones ornamentales, como podemos
observar en los siguientes ejemplos:

52. 3.-TRANSFORMACIONES GEOMÉTRICAS
Las transformaciones geométricas son modificaciones sobre formas
geométricas o figurativas. Al llevar a cabo estas transformaciones se mantienen los
valores básicos de las figuras, aunque se producen variaciones en sus medidas, posición u
orientación. Este curso veremos las siguientes transformaciones geométricas:
-Semejanza
-Traslación
-Simetría
a)Semejanza: dos figuras son semejantes o proporcionales cuando, sus formas
son iguales, pero varían sus medidas (la figura resultante es más grande o más pequeña,
pero sigue conservando la misma forma). Existen varios procedimientos para dibujar una
figura semejante a otra, veremos a continuación uno de ellos.
Figuras semejantes

53. 1.-Queremos hacer una figura semejante a la figura ABCD y que mida el
doble de ésta. Para ello, situamos un punto P exteriormente a la misma.
2.-Unimos P con todos los vértices, prolongando dichas rectas

54. 3.-Medimos la distancia desde P a cada uno de los vértices, y pasamos esa medida a
la prolongación da cada una de las rectas, a partir del vértice.
4.-Solo nos resta unir cada uno de los puntos obtenidos para obtener una figura
semejante a la dada, pero con el doble de tamaño.

55. Si queremos obtener una figura a la mitad de tamaño, en lugar de tomar la distancia desde
P hasta los vértices, tomamos la mitad de la distancia desde P a cada uno de ellos:

56. b)Traslación: consiste en desplazar una figura en una cierta dirección, resultando
una figura exactamente igual que la original, pero en otra posición. Para trasladar una
figura se trazan por sus vértices líneas paralelas y, sobre estas líneas, se marca la distancia
a la que se quiera obtener la nueva figura. Si nos dan ya la dirección, o un punto de la
nueva figura, solo hay que trazar paralelas a esa dirección y marcar la distancia.

57. 1.-Partimos de una figura cualquiera.
En este caso, nos dan un punto A’ de
la nueva figura y una dirección d.
2.-Desde cada uno de los vértices,
trazamos paralelas a la dirección d,
a la misma distancia que AA’.
3.-Solo nos resta unir los puntos obtenidos
para obtener la nueva figura, igual a la anterior
pero en una nueva posición.

58. 4.-Simetría: dos figuras son simétricas respecto a un eje (eje de
simetría) cuando todos sus puntos está situados a la misma
distancia de este eje, sobre rectas perpendiculares a éste y
equidistan de él

59. 1.-Partimos de la figura
dada y de un eje de
simetría situado a su
derecha
2.-Trazamos perpendiculares
al eje pasando por los
vértices y trasladamos la
distancia de cada vértice al
eje a la prolongación de
estas perpendiculares.
3.-Unimos los puntos
obtenidos, con lo que
tenemos la nueva figura,
simétrica a la dada.