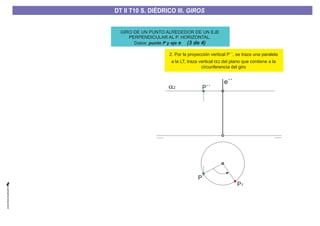
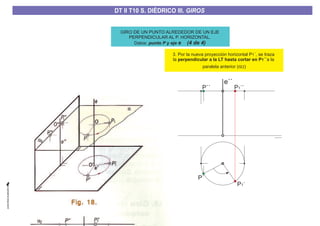
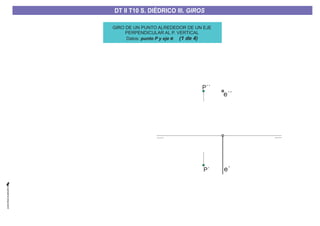
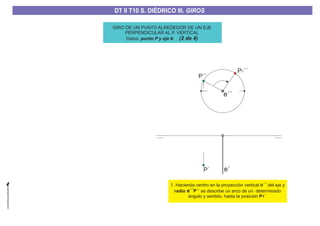
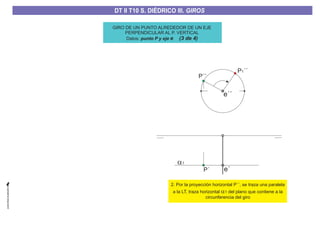
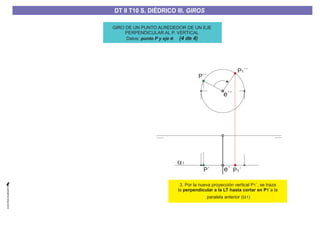
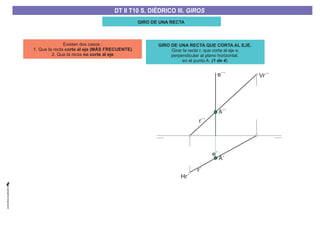
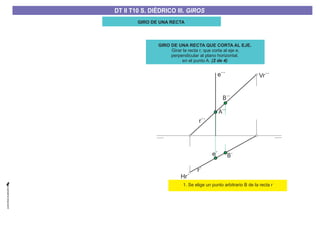
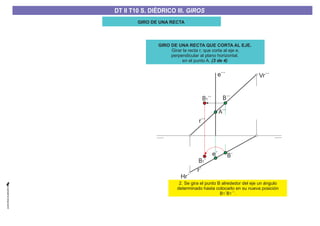
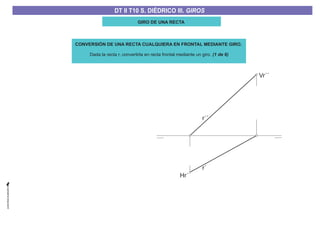
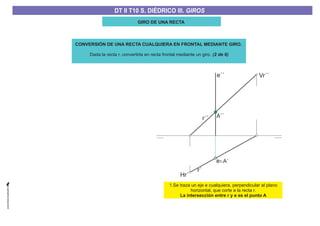
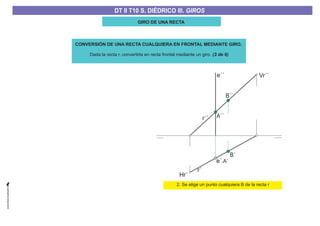
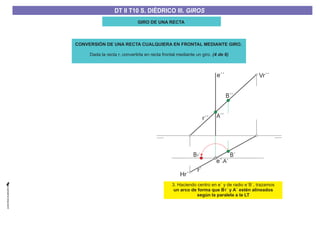
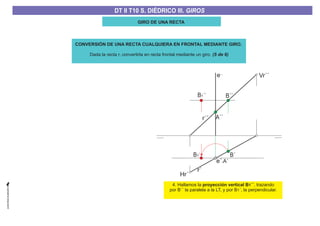
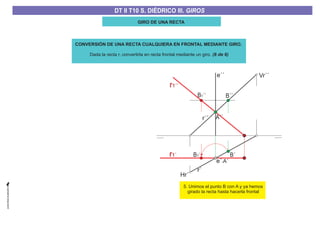
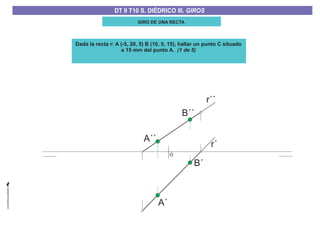
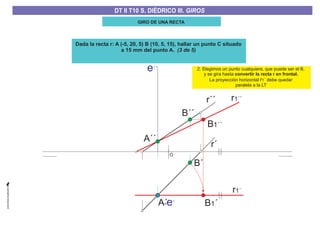
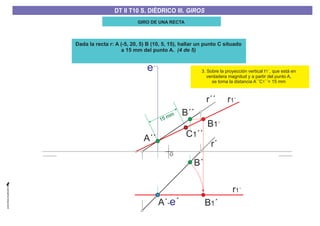
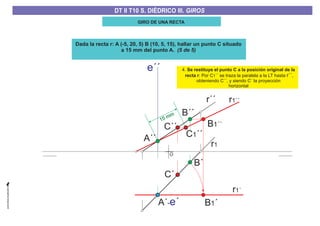
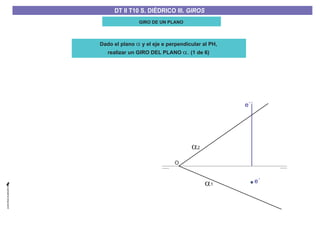
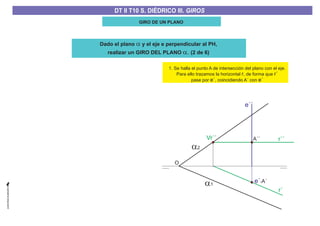
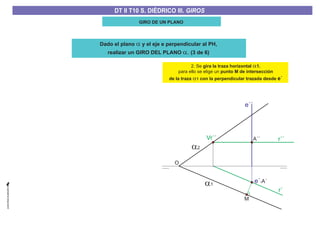
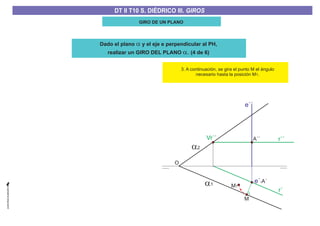
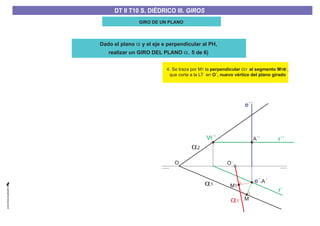
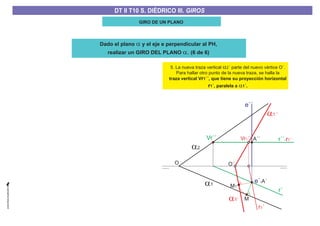
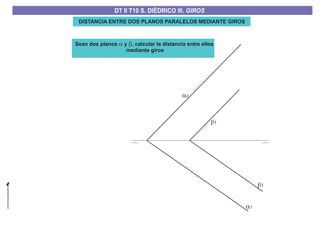
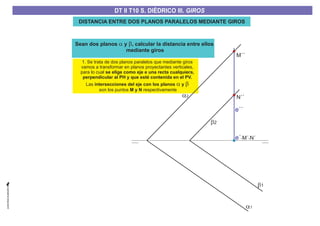
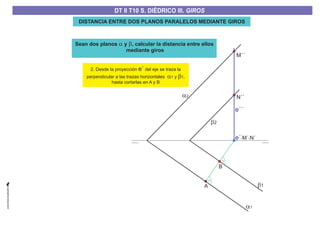
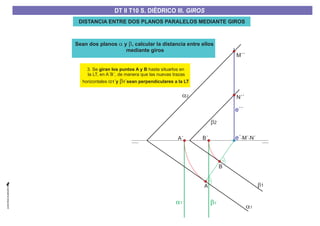
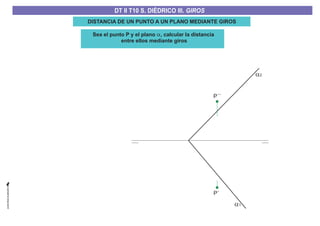
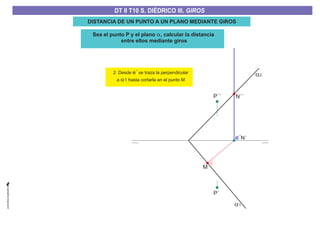
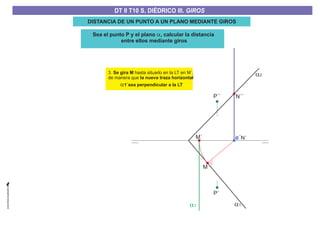
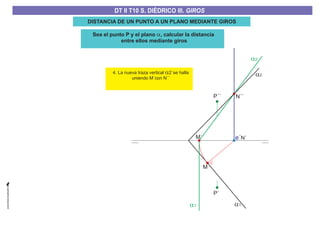
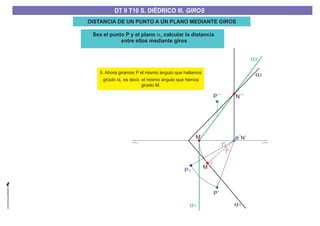
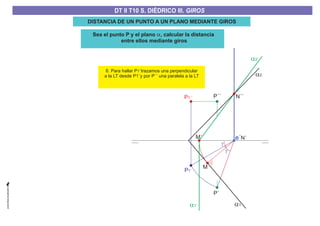
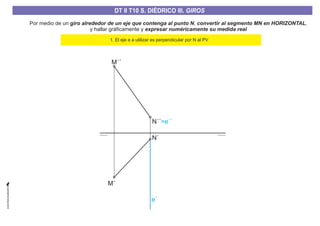
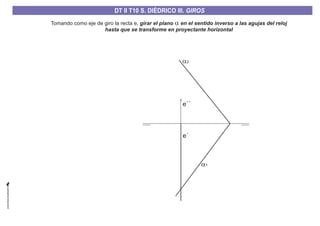
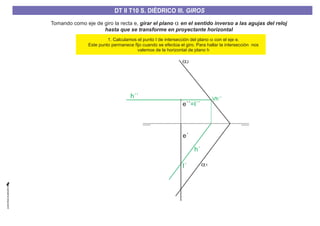
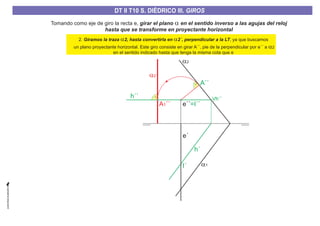
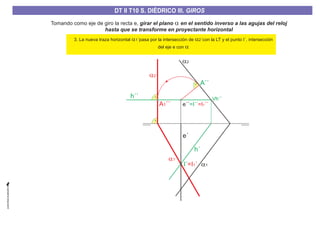
El documento aborda el concepto de giros en dibujo técnico, específicamente el giro de puntos y rectas alrededor de ejes perpendiculares al plano horizontal y vertical. Se detallan diferentes enfoques y pasos para interpretar y realizar estos giros mediante proyecciones que permiten transformar las posiciones de los elementos geométricos. Además, se analizan casos donde las rectas pueden cortar o no cortar el eje y cómo convertir rectas ordinarias en rectas frontales mediante giros.