El capítulo 2 sobre canales inalámbricos analiza modelos de propagación, como el espacio libre y la tierra plana, que predicen la intensidad de la señal en función de la distancia entre el transmisor y el receptor. Destaca la pérdida de trayectoria y su relación con la potencia transmitida y recibida, y proporciona ejemplos prácticos de cálculo, incluyendo transformaciones a decibelios. Además, explora la influencia de factores como la reflexión en la propagación de señales en entornos urbanos y rurales.


![Inverse-square law (caso general - física)
S → fuente.
r → puntos de medición.
Lineas → flujo que emana de la
fuente.
El número total de líneas de flujo
depende la intensidad de la
fuente y es constante respecto al
incremento de la distancia.
Gran densidad de líneas de flujo
(líneas por unidad de área)
significa un campo fuerte.
A
A
Ar
2r
S
3r
Referencia: [Wikipedia, 2016a]
La densidad de líneas de flujo es inversamente proporcional al
cuadrado de la distancia de la fuente al punto de medición, porque el
área de la superficie de la esfera incrementa con el cuadrado del radio.
La intensidad del campo es inversamente proporcional al cuadrado de
la distancia de la fuente al punto de medición.
fasandoval@utpl.edu.ec CI CI-Large-Scale Path Loss 4 / 68](https://image.slidesharecdn.com/blargescalepathlossresumen2019-200106134114/85/CI19-2-Presentaciones-Large-scale-path-loss-4-320.jpg)
![Modelo de Propagación en Espacio Libre (PEL)
Ecuación de espacio libre de Friis
El modelo de espacio libre predice la intensidad de señal
recibida cuando el trayecto de propagación Tx–Rx es sin
obstrucciones (LOS).
Gobernado por la ecuación de espacio libre de Friis
Pr(d) =
PtGtGrλ2
(4π)2d2L
(1) Tx Rx
Pr(d) y Pt → Potencia Rx (función de d) y potencia Tx.
Gt y Gr → Ganancia de la antena de Tx y Rx.
λ → longitud de onda [metros].
d → distancia Tx–Rx [metros].
L ≥ 1 → Factor de pérdida del sistema (no relacionado con la
propagación).
fasandoval@utpl.edu.ec CI CI-Large-Scale Path Loss 5 / 68](https://image.slidesharecdn.com/blargescalepathlossresumen2019-200106134114/85/CI19-2-Presentaciones-Large-scale-path-loss-5-320.jpg)
![Modelo de Propagación en Espacio Libre
Acotaciones: Ecuación de espacio libre de Friis
La ganancia de la antena está relacionada con la apertura efectiva Ae
G =
4πAe
λ2
(2)
La apertura efectiva Ae esta relacionada con el tamaño físico de la antena.
λ esta relacionado con la frecuencia
λ =
c
f
=
2πc
ωc
f → frecuencia de la portadora [Hertz]
ωc → portadora de la frecuencia [radianes por segundo]
c → velocidad de la luz [m/s]
Pt y Pr se expresa en unidades similares.
Gt y Gr son adimensionales.
L → Atenuación en la línea de transmisión, pérdidas en filtros, y
antenas del sistema de comunicación.
L = 1 → no existe pérdidas en el hardware del sistema.
fasandoval@utpl.edu.ec CI CI-Large-Scale Path Loss 6 / 68](https://image.slidesharecdn.com/blargescalepathlossresumen2019-200106134114/85/CI19-2-Presentaciones-Large-scale-path-loss-6-320.jpg)
![Effective isotropic radiaded power (EIRP)
Radiador isotrópico: antena ideal que radia potencia con
ganancia unitaria uniformemente en todas las direcciones.
Se emplea (usualmente) como referencia de la ganancia de
la antena en un sistema inalámbrico.
Potencia isotrópica radiada equivalente (effective isotropic
radiaded power) [EIRP]: cantidad de potencia que emitiría
una antena isotrópica teórica para producir la densidad de
potencia observada en la dirección de máxima ganancia de
una antena.
EIRP = PtGt
En la práctica la ganancia de una antena es dada en
unidades de dBi (ganancia en dB respecto a una fuente
isotrópica).
fasandoval@utpl.edu.ec CI CI-Large-Scale Path Loss 7 / 68](https://image.slidesharecdn.com/blargescalepathlossresumen2019-200106134114/85/CI19-2-Presentaciones-Large-scale-path-loss-7-320.jpg)
![Pérdida en trayectoria (Path Loss)
Representa la atenuación de la señal como una cantidad
positiva medida en dB.
Es la diferencia (en dB) entre la potencia efectiva
transmitida y la potencia recibida y puede o no incluir el
efecto de las ganancias de las antenas.
PL[dB] = 10 log
Pt
Pr
= −10 log
GtGrλ2
(4π)2d2
Si no se considera el efecto de las antenas (asumen
ganancia unitaria):
PL[dB] = 10 log
Pt
Pr
= −10 log
λ2
(4π)2d2
fasandoval@utpl.edu.ec CI CI-Large-Scale Path Loss 8 / 68](https://image.slidesharecdn.com/blargescalepathlossresumen2019-200106134114/85/CI19-2-Presentaciones-Large-scale-path-loss-8-320.jpg)
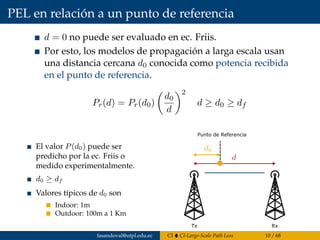
![Validez de la Ec. de Friis
El modelo de espacio libre de Friis es válido para valores de d
correspondientes a campo lejano (far-field) de la antena de transmisión.
d ≥ df , df es la distancia Fraunhofer o far-field.
Para antenas electromagnéticamente largas (ej: ant. radar - directivas) es:
df =
2D2
λ
D → mayor dimensión lineal física de la antena.
df debe satisfacer: df >> D and df >> λ.
Source
1 wavelength
NEAR-FIELD REGION
reactive radiative
TRANSITION ZONE FAR-FIELD REGION
The maximum overall
dimension of the source
antenna 5D5 is a prime
factor in determining
this boundary
The far-field generally
starts at a distance
of 2D²/λ out to infinity
x
λ/2π
=
0.159
wavelength
2 wavelengths from 2 wavelengths to infinity
Referencia: [Wikipedia, 2016b]
Región de campo para antena electromagnéticamente corta (ej. AM broadcast).
fasandoval@utpl.edu.ec CI CI-Large-Scale Path Loss 9 / 68](https://image.slidesharecdn.com/blargescalepathlossresumen2019-200106134114/85/CI19-2-Presentaciones-Large-scale-path-loss-9-320.jpg)



![Ejemplo: Transformación a dBs
Si un transmisor produce 50 Watts de potencia, exprese la
potencia transmitida en unidades de (a) dBm, y (b) dBW.
Solución:
Parámetros:
Potencia transmitida: Pt = 50 W
(a) Potencia transmitida (dBm)
Pt( dBm) = 10 log[Pt(W)/(1 mW)]
= 10 log[50 · 10−3
]
= 47.0 dBm
Potencia transmitida (dBW)
Pt( dBW) = 10 log[Pt(W)/(1 W)]
= 10 log[50]
= 17.0 dBW
fasandoval@utpl.edu.ec CI CI-Large-Scale Path Loss 12 / 68](https://image.slidesharecdn.com/blargescalepathlossresumen2019-200106134114/85/CI19-2-Presentaciones-Large-scale-path-loss-14-320.jpg)


![Operaciones con dB
Importante: Las siguientes operaciones pueden realizarse:
dBW ± dB = dBW
dBm ± dB = dBm
dBW − dBW = dB
dBm − dBm = dB
Por el contrario:
Nunca multiplique dBW con dB.
PT · GT = 10 W · 10 = 100 W 20 dBW
⇔ PT [ dBW] + GT [ dBi] = 10 dBW + 10 dBi = 20 dBW
Nunca sume varias cantidades en dBW o dBm.
10 dBW + 3 dBW + 6 dBW 10 W · 2 W · 4 W = 80 W3
¿Qué unidad es W3
?...???
La potencia no puede ser medida en dB.
Las ganancias/pérdidas no pueden ser medidas en dBm o dBW.
fasandoval@utpl.edu.ec CI CI-Large-Scale Path Loss 14 / 68](https://image.slidesharecdn.com/blargescalepathlossresumen2019-200106134114/85/CI19-2-Presentaciones-Large-scale-path-loss-17-320.jpg)


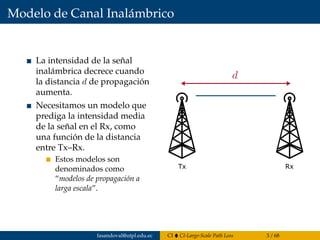
![Modelo de Tierra Plana
Para distancias cortas (se puede despreciar la curvatura
terrestre [decenas de Kms]) + Terreno liso.
Para f < 150MHz, alturas de antenas reducidas y
polarización vertical, considerar también la onda de
superficie (adicional a RD y RR).
La OdS es dominante para f < 10 MHz, polarización
vertical (antena Tx monopolo) y terreno buen conductor
(metodología propia de cálculo - no aplica MTP).
fasandoval@utpl.edu.ec CI CI-Large-Scale Path Loss 17 / 68](https://image.slidesharecdn.com/blargescalepathlossresumen2019-200106134114/85/CI19-2-Presentaciones-Large-scale-path-loss-20-320.jpg)
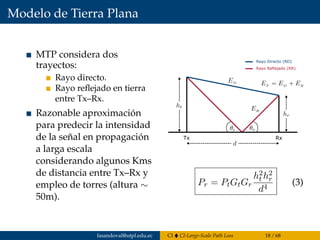
![Modelo de Tierra Plana
La potencia recibida en MTP decae respecto a la cuarta
potencia de la distancia entre Tx–Rx.
En MTP la potencia recibida decae mucho más rápido que
en espacio libre (d2).
La pérdida por trayectoria en el MTP en dB puede
expresarse como:
PL[dB] = 40 log d − (10 log Gt + 10 log Gr + 20 log ht + 20 log hr)
fasandoval@utpl.edu.ec CI CI-Large-Scale Path Loss 19 / 68](https://image.slidesharecdn.com/blargescalepathlossresumen2019-200106134114/85/CI19-2-Presentaciones-Large-scale-path-loss-22-320.jpg)




![Propagación por Difracción
Obstáculos en la propagación.
Según el modelo sencillo de óptica geométrica, no habría
propagación.
7.6 Propagación por difracción
Problema
• La propagación encuentra un obstáculo:
Por el modelo sencillo de óptica geométrica no habría propagación
Si recurrimos a un modelo más exacto se comprueba que sí es posible
Objetivos: modelar este fenómeno y calcular las pérdidas
- para obstáculos agudos o redondeados, aislados ó múltiples
- y ver cómo se trabaja en la práctica
Referencia: [Murillo, 2008]
Considerando un modelo más exacto, se comprueba que si es
posible.
7.6 Propagación por difracción
Problema
• La propagación encuentra un obstáculo:
Por el modelo sencillo de óptica geométrica no habría propagación
Si recurrimos a un modelo más exacto se comprueba que sí es posible
Objetivos: modelar este fenómeno y calcular las pérdidas
- para obstáculos agudos o redondeados, aislados ó múltiples
- y ver cómo se trabaja en la práctica
Referencia: [Murillo, 2008]
Problema a resolver:
Modelar este fenómeno.
Calcular las pérdidas para obstáculos agudos, redondeados,
aislados o múltiples.
fasandoval@utpl.edu.ec CI CI-Large-Scale Path Loss 24 / 68](https://image.slidesharecdn.com/blargescalepathlossresumen2019-200106134114/85/CI19-2-Presentaciones-Large-scale-path-loss-28-320.jpg)
![Difracción
Difracción (física)
“Fenómeno característico de ondas que se basa en la desviación de estas al
encontrar un obstáculo o al atravesar una rendija” [wikipedia].
Principio de Huygens
“Todo punto de un frente de onda inicial puede considerarse como una
fuente de ondas esféricas secundarias que se extienden en todas las
direcciones con la misma velocidad, frecuencia y longitud de onda que el
frente de onda del que proceden” [wikipedia].
La difracci´on
El principio de Huygens exprime el hecho de que un frente de onda
se comporta como una fuente secundaria para formar un nuevo
frente de onda.
Referencia: [Wagemakers and Borja, a]
fasandoval@utpl.edu.ec CI CI-Large-Scale Path Loss 25 / 68](https://image.slidesharecdn.com/blargescalepathlossresumen2019-200106134114/85/CI19-2-Presentaciones-Large-scale-path-loss-29-320.jpg)
![Difracción
Cuando la onda intercepta
un obstáculo, éste se
convierte en una fuente
secundaria.
Si el obstáculo consiste en
una barrera
Un nuevo frente de onda
se forma (deformado).
Los objetos situados
detrás de la barrera
pueden recibir la onda.
Como consecuencia del principio de difracci´on, cuando la onda
intercepta un obst´aculo, el obst´aculo se convierte en una fuente
secundaria. Aqu´ı tenemos la difracci´on por una apertura peque˜na
frente a la longitud de onda.
Referencia: [Wagemakers and Borja, a].
Difracción por una apertura pequeña frente a la longitud
de onda.
La difracci´on
Si el obst´aculo consiste en una barrera, un nuevo frente de onda se
forma, este esta deformado por objetos situados detr´as de esta
barrera pueden recibir la onda.
Referencia: [Wagemakers and Borja, a].
Difracción cuando el obstáculo consiste en una barrera.
fasandoval@utpl.edu.ec CI CI-Large-Scale Path Loss 26 / 68](https://image.slidesharecdn.com/blargescalepathlossresumen2019-200106134114/85/CI19-2-Presentaciones-Large-scale-path-loss-30-320.jpg)
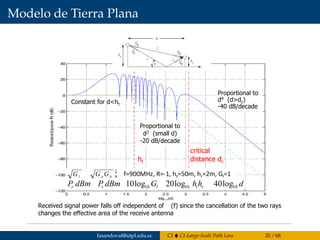
![Difracción
¿Qué pasa si llegan fases opuestas?
Aunque llega atenuada, por tener mayor trayecto, contribuye
negativamente en recepción.
Tx Rx
Las trayectorias con fases opuestas marcan distintas zonas de Fresnel.
El campo en Rx coincide en primera aproximación con la contribución
de la primera zona de Fresnel. Referencia: [Murillo, 2008]
fasandoval@utpl.edu.ec CI CI-Large-Scale Path Loss 27 / 68](https://image.slidesharecdn.com/blargescalepathlossresumen2019-200106134114/85/CI19-2-Presentaciones-Large-scale-path-loss-31-320.jpg)
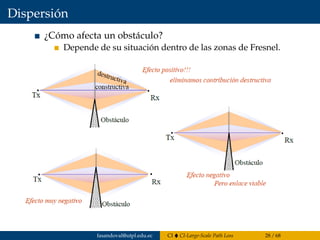
![Zonas de Fresnel
Los puntos de reflexión/difracción destructiva pueden ser identificados
definiendo el término rn (radio de las zonas de Fresnel)
rn =
nλd1d2
d1 + d2
La reflexión/difracción en el punto rn para valores impares de n causa
interferencia destructiva.
Ya que, la diferencia en longitud de la trayectoria es en el orden de λ, la
señal reflejada/difractada puede ser tan fuerte como el RD y causar la
cancelación.
La ecuación rn define una secuencia de elipsoides con el Tx y el Rx en
los focos.
The destructive reflection/diffraction points can then be identified by defining
a term, hn, such that
(8.20)
Reflectors/diffraction at hn for odd values of n will cause destructive interfer-
ence. Since the difference in path lengths is on the order of l, the reflected/dif-
fracted signal may be as strong as the direct signal and cause cancellation.
The equation for hn defines a sequence of ellipsoids with the transmit and
receive antennas as the foci. Diffractors or reflectors at the odd-numbered
Fresnel zone boundaries will cause destructive interference. Figure 8.8 shows
a diagram of the Fresnel zones defined by a point-to-point link. Note that this
diagram is two-dimensional, whereas the actual Fresnel zones are three-
dimensional ellipsoids. For large h or small d1 and d2, the antenna pattern may
attenuate the undesired signal. For omnidirection (vertical) antennas, there
may be attenuation of the undesired signal in elevation, but not in azimuth.
From the preceding analysis, it is clear that any reflectors/diffractors within
the field of view should not be near an odd Fresenel zone boundary to avoid
signal loss. It is also important that the first Fresnel zone be clear of obstruc-
tions because this can seriously degrade the available signal energy. Due to
Huygen’s principle, covered in the next section, the diffracted electromagnetic
energy that fills the shadow at the receive end of the link reduces the energy
that arrives at the receiver. If the first Fresnel zone is not clear, then free-space
loss does not apply and an adjustment term must be included. For most appli-
h
n d d
d d
n =
+
l 1 2
1 2
A B
Third Fresnel
Zone
Fourth Fresnel
Zone
Second Fresnel Zone
First Fresnel Zone
Figure 8.8 Fresnel zones between a transmitter and receiver.
Referencia: [Seybold, 2005]
T R
Referencia: [Murillo, 2008]
fasandoval@utpl.edu.ec CI CI-Large-Scale Path Loss 29 / 68](https://image.slidesharecdn.com/blargescalepathlossresumen2019-200106134114/85/CI19-2-Presentaciones-Large-scale-path-loss-33-320.jpg)
![Zonas de Fresnel
La primera zona de Fresnel debe permanecer sin obstrucción porque
puede causar serias degradaciones en la energía de la señal disponible.
Si la primera zona de Fresnel no está despejada, el modelo de espacio
libre no puede ser aplicado y es necesario incluir un término de ajuste.
Para la mayoría de aplicaciones, tener despejado el 60% de la primera
zona de Fresnel es suficiente.
El punto 0.6h corresponde al valor v = −0.8 del parámetro de
difracción de Fresnel-Kirchhoff y resulta en pérdida por difracción de
0dB.
v es negativo → el RD no está obstruido.
178 FADING AND MULTIPATH CHARACTERIZATION
A B
h
0.6h
0.4h
First Fresnel
Zone Ellipsoid
Maximum
Allowable
Blockage
Keep Clear
Figure 8.9 Fresnel zone blockage geometry.
Referencia: [Seybold, 2005]
fasandoval@utpl.edu.ec CI CI-Large-Scale Path Loss 30 / 68](https://image.slidesharecdn.com/blargescalepathlossresumen2019-200106134114/85/CI19-2-Presentaciones-Large-scale-path-loss-34-320.jpg)



![Cálculo de las pérdidas por difracción
Obstáculos (−0.6r1 < h, f > 30MHz):
1era aproximación:
Obstáculo agudo (OAg) o filo de cuchillo (Knife-edge).
Obstáculo redondeado (ORe), definido por el radio de
curvatura en la cima r
Se considera también:
Obstáculo aislado.
Obstáculos múltiples.
Referencia: [Seybold, 2005]
fasandoval@utpl.edu.ec CI CI-Large-Scale Path Loss 33 / 68](https://image.slidesharecdn.com/blargescalepathlossresumen2019-200106134114/85/CI19-2-Presentaciones-Large-scale-path-loss-38-320.jpg)

![Obstáculo Agudo
Referencia: [Murillo, 2008]
fasandoval@utpl.edu.ec CI CI-Large-Scale Path Loss 35 / 68](https://image.slidesharecdn.com/blargescalepathlossresumen2019-200106134114/85/CI19-2-Presentaciones-Large-scale-path-loss-40-320.jpg)
![Ejemplo: Obstáculo Agudo
Considere un enlace de comunicación entre dos radios de mano a f = 150MHz según
el esquema. Calcular las pérdidas de propagación debido a la difracción.
Since the blockage is below the line of sight, the values of h and v are neg-
ative. The following parameters are known:
Using the expression for the Fresnel–Kirchhoff diffraction parameter, (8.19),
yields
From the plot in Figure 8.12, the diffraction loss can be estimated as 0.75 or
-2.5dB, or the Lee approximation to the diffraction integral can be used
directly to get
n = -0 395.
h
d d
= - =
= =
5 2
200 8001 2
m m
m m
,
,
l
182 FADING AND MULTIPATH CHARACTERIZATION
Figure 8.13 Knife-edge diffraction geometry for Example 8.3.Referencia: [Seybold, 2005]
fasandoval@utpl.edu.ec CI CI-Large-Scale Path Loss 36 / 68](https://image.slidesharecdn.com/blargescalepathlossresumen2019-200106134114/85/CI19-2-Presentaciones-Large-scale-path-loss-41-320.jpg)
![Ejemplo: Obstáculo Agudo
Considere un enlace de comunicación entre dos radios de mano a f = 150MHz según
el esquema. Calcular las pérdidas de propagación debido a la difracción.
Since the blockage is below the line of sight, the values of h and v are neg-
ative. The following parameters are known:
Using the expression for the Fresnel–Kirchhoff diffraction parameter, (8.19),
yields
From the plot in Figure 8.12, the diffraction loss can be estimated as 0.75 or
-2.5dB, or the Lee approximation to the diffraction integral can be used
directly to get
n = -0 395.
h
d d
= - =
= =
5 2
200 8001 2
m m
m m
,
,
l
182 FADING AND MULTIPATH CHARACTERIZATION
Figure 8.13 Knife-edge diffraction geometry for Example 8.3.Referencia: [Seybold, 2005]
Solución:
Parámetros:
h = −5m, λ = 2m.
d1 = 200m, d2 = 800m.
Calcular v
v = h
2(d1 + d2)
λd1d2
= −0.395.
A través de la figura se puede estimar Ld o a través de la aproximación de Lee:
Ld = 20 log(0.5 − 0.62v) = −2.6 dB
fasandoval@utpl.edu.ec CI CI-Large-Scale Path Loss 36 / 68](https://image.slidesharecdn.com/blargescalepathlossresumen2019-200106134114/85/CI19-2-Presentaciones-Large-scale-path-loss-42-320.jpg)

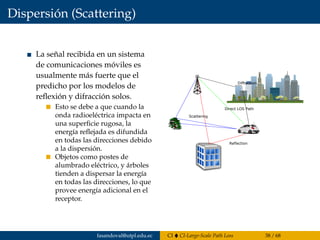

![Clasificación de los entornos urbanos
Los problemas de propagación dependen fuertemente del
entorno.
En general se clasifica el entorno en cuatro clases:
Zona rural.
Sub-urbano.
Urbano.
Urbano denso.
Se puede desarrollar modelos específicos para cada tipo de
entorno.
Existen clasificaciones más objetivas donde intervienen:
La densidad de superficie de los edificios.
El volumen medio de los edificios.
Altura media, etc.
Tomado de: [Wagemakers and Borja, b].
fasandoval@utpl.edu.ec CI CI-Large-Scale Path Loss 40 / 68](https://image.slidesharecdn.com/blargescalepathlossresumen2019-200106134114/85/CI19-2-Presentaciones-Large-scale-path-loss-46-320.jpg)
![Clasificación de los entornos urbanosClasificaci´on de entornos urbanos
Definiciones sacadas de la norma ITU-R P1411-3.
Tomado de: [Wagemakers and Borja, b].
fasandoval@utpl.edu.ec CI CI-Large-Scale Path Loss 41 / 68](https://image.slidesharecdn.com/blargescalepathlossresumen2019-200106134114/85/CI19-2-Presentaciones-Large-scale-path-loss-47-320.jpg)
![Clasificación de los entornos urbanos
Tomado de: [Wagemakers and Borja, b].
fasandoval@utpl.edu.ec CI CI-Large-Scale Path Loss 42 / 68](https://image.slidesharecdn.com/blargescalepathlossresumen2019-200106134114/85/CI19-2-Presentaciones-Large-scale-path-loss-48-320.jpg)
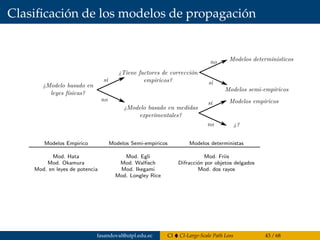

![Modelos empíricos y semi-empíricos
Varios modelos han sido desarrollados para modelar la
intensidad de señal recibida en escenarios prácticos de
comunicaciones inalámbricas urbanas.
Los modelos empíricos de pérdidas en variados entornos
son construidos a partir de medidas realizadas in situ.
Reflejan la realidad y pueden dar una idea del peor caso.
Modelos empiricos y semi-empiricos
Se han construidos modelos empiricos de perdidas en entornos
variados a partir de medidas realizadas in situ. Estos modelos
reflejan la realidad y pueden dar una idea del peor caso, es decir
una cuato superior razonable para las perdidas.
En la figura se presenta un ejemplo de como se ajustan medidas
Ejemplo de ajuste de medidas experimentales a un modelo a trozos.
Referencia: [Wagemakers and Borja, b]
fasandoval@utpl.edu.ec CI CI-Large-Scale Path Loss 45 / 68](https://image.slidesharecdn.com/blargescalepathlossresumen2019-200106134114/85/CI19-2-Presentaciones-Large-scale-path-loss-51-320.jpg)



![Modelo Okumura
oubt, check the results using known test cases, or engineering judgment. For
nstance, if increasing the antenna height increases the median path loss, then
he sign of the antenna height correction factor is clearly reversed.
Figure 7.9 shows plots of Amu versus frequency for various distances. Figure
.10 shows the base station height gain factor in urban areas versus effective
100
10
20
30
40
BasicmedianattentuationAmu(f,d)(dB)
50
60
70
hm = 3 m
hb = 200 m
Urban area
200 300 500
Frequency f (MHz)
700 1000 2000 3000
100
100
80
80
60
60
50
50
40
40
30
30
20
20
10
10
5
5
2
2
1
1 d(km)
igure 7.9 Plot of Amu versus frequency for use with the Okumura model. (Figure 4.7
Ref. 13, courtesy of Wiley.)Gráfica de Amu versus frecuencia.
Referencia: [Seybold, 2005]
height for various distances, while Figure 7.11 shows the vehicle antenna
height gain factor versus effective antenna height for various frequencies and
levels of urbanization. Figure 7.12 shows how the base station antenna height
is measured relative to the mean terrain height between 3 and 15km in the
direction of the receiver.
Example 7.4. Consider a system with the following parameters:
PROPAGATION IN BUILT-UP AREAS 149
30
20
10
–10
–20
–30
20 30 50
Base station effective antenna height hte (m)
70 100 200 300 500 700 1000
0
d (km)
d(km)
100
80
70
60
50
40
20
1
3
5
10
70~
100
60
40
20
1~10
HeightgainfactorHtu(hte,d)(dB)
Urban area
hte = 200 m
Figure 7.10 Plot of Htu, the base station height correction factor, for the Okumura
model. (Figure 4.8 from Ref. 13, courtesy of Wiley.)
Gráfica de Htu, el factor de corrección de la altura de la
BS.
Referencia: [Seybold, 2005]
fasandoval@utpl.edu.ec CI CI-Large-Scale Path Loss 49 / 68](https://image.slidesharecdn.com/blargescalepathlossresumen2019-200106134114/85/CI19-2-Presentaciones-Large-scale-path-loss-55-320.jpg)
![Modelo Okumura
150 NEAR-EARTH PROPAGATION MODELS
2000
1000
700
400
200
100
100
200
400~
1000
20
15
10
AntennaheightgainfactorHru(hre,f)(dB)
5
0
–5
1 2 3 5 7 10
Vehicular station antenna height hre (m)
400 MHz
200 MHz
Urban area
MediumcityLargecity
f(MHz)
Figure 7.11 Plot of Hru, the mobile station height correction factor for the Okumura
model. (Figure 4.9 from Ref. 13, courtesy of Wiley.)
h te
h t
h
Gráfica de Hru, el factor de corrección de la altura de la
estación móvil.
Referencia: [Seybold, 2005]
200
400~
1000
Antennaheightgainf
5
0
–5
1 2 3 5 7 10
Vehicular station antenna height hre (m)
400 MHz
200 MHz
Large
Figure 7.11 Plot of Hru, the mobile station height correction factor for the Okumura
model. (Figure 4.9 from Ref. 13, courtesy of Wiley.)
3 km 15 km
Average height
h te
h t
h
Figure 7.12 Measuring effective transmitter height. (Figure 4.10 from Ref. 13, cour-
tesy of Wiley.)
Medida de la altura efectiva del transmisor. Altura de
antena de la BS relativo a la altura media del terreno entre
3 y 15 Km en dirección del Rx.
Referencia: [Seybold, 2005]
fasandoval@utpl.edu.ec CI CI-Large-Scale Path Loss 50 / 68](https://image.slidesharecdn.com/blargescalepathlossresumen2019-200106134114/85/CI19-2-Presentaciones-Large-scale-path-loss-56-320.jpg)


![Modelo Hata
El modelo Hata (a veces llamado modelo Okumura-Hata) presenta una
aproximación analítica para la información gráfica provista por el
modelo Okumura.
Existen tres fórmulas diferentes para áreas: urbanas, sub-urbanas y
abiertas.
Áreas urbanas
L50(dB) = 69.55 + 26.16 log(fc) − 13.82 log(ht) − a(hr)
+ [44.9 − 6.55 log(ht)] log(d)
donde
150 < fc < 1500, fc en MHz.
30 < ht < 200, ht en m.
1 < d < 20, d en Km.
a(hr) → factor de corrección de la altura de la antena del móvil. Para
ciudades pequeñas o medianas:
a(hr) = (1.1 log(fc) − 0.7)hr − (1.56 log(fc) − 0.8); 1 ≤ hr ≤ 10 m
y para ciudades grandes:
a(hr) =
8.29(log(1.54hr))2 − 1.1, fc ≤ 200 MHz
3.2(log(11.75hr))2 − 4.97, fc ≤ 400 MHz
fasandoval@utpl.edu.ec CI CI-Large-Scale Path Loss 52 / 68](https://image.slidesharecdn.com/blargescalepathlossresumen2019-200106134114/85/CI19-2-Presentaciones-Large-scale-path-loss-59-320.jpg)


![Ejemplo: Modelo Hata
Considere el sistema con los siguientes parámetros:
ht = 68 m
hr = 3 m
f = 870 MHz, λ = 0.345 m
d = 3.7 m
¿Cuál es la pérdida de trayectoria predicha usando el modelo de Okumura?
Solución:
L50dB = 69.55 + 26.16 log(870) − 13.82 log(68) − a(hr)
+ [44.9 − 6.55 log(68)] log(3.7)
donde el factor de corrección de la altura de la antena (asumiendo una
ciudad grande) es
a(3) = 3.2(log(11.75 · 3))2
− 4.97 = 2.69
El resultado final es L50(dB) = 137.1 dB, que difiere del ejemplo anterior por
7.4.
fasandoval@utpl.edu.ec CI CI-Large-Scale Path Loss 54 / 68](https://image.slidesharecdn.com/blargescalepathlossresumen2019-200106134114/85/CI19-2-Presentaciones-Large-scale-path-loss-62-320.jpg)

![Modelo Cost 231
Las pérdidas por trayectoria (mediana) es dada por:
L50(dB) = 46.3 + 33.9 log(fc) − 13.82 log(ht) − a(hr)
+ [44.9 − 6.55 log(ht)] log(d) + C
donde
fc → frecuencia en MHz.
ht → la altura de la estación base en metros.
hr → la altura de la estación móvil en metros.
a(hr) → factor de corrección de la altura de la antena móvil
definido anteriormente.
d → es la distancia del enlace en Km.
C = 0 dB para ciudades medianas o centros sub-urbanos
con densidad media de árboles.
C = 3 dB para centros metropolitanos.
fasandoval@utpl.edu.ec CI CI-Large-Scale Path Loss 56 / 68](https://image.slidesharecdn.com/blargescalepathlossresumen2019-200106134114/85/CI19-2-Presentaciones-Large-scale-path-loss-64-320.jpg)







![Ejemplo: Balance del Enlace
Considere el siguiente escenario: radio de la célula d = 8 Km, frecuencia portadora
fc = 2.1 GHz, altura de la antena de Tx ht = 40 m, altura de la antena Rx hr = 2 m,
margen requerido igual a 10 dB, T = 293 K, ancho de banda B = 30 KHz, noise figure
5 dB, la ganancia de la antena de Rx Gr = 5 dB, las pérdidas por cables Lc = 3 dB, la
ganancia de la antena de Tx Gt = 12 dB, y la potencia de interferencia es igual a la
potencia de ruido. Calcule la potencia de transmisión requerida considerando un BER
= 10−4 para BPSK en el receptor.
Solución:
1 Cálculo de las pérdidas por trayectoria empleando el modelo Hata para ciudad
grande:
a(hr) = 3.2 (log10(11.75 × 2))2
− 4.97
= 1.04 dB
L50(dB) = 69.55 + 26.16 log(fc) − 13.82 log(ht) − a(hr)
+ [44.9 − 6.55 log(ht)] log(d)
L50(dB) = 69.55 + 26.16 log(2100) − 13.82 log(2) − 1.04
+ [44.9 − 6.55 log(2)] log(8)
L50 = 69.55 + 86.90 − 22.14 − 1.04 + 31.07
= 164.34 dB
fasandoval@utpl.edu.ec CI CI-Large-Scale Path Loss 64 / 68](https://image.slidesharecdn.com/blargescalepathlossresumen2019-200106134114/85/CI19-2-Presentaciones-Large-scale-path-loss-73-320.jpg)



![References I
[Murillo, 2008] Murillo, J. (2008).
Radiación y radiocomunicación.
[Seybold, 2005] Seybold, J. S. (2005).
Introduction to RF propagation.
John Wiley & Sons.
[Wagemakers and Borja, a] Wagemakers, A. and Borja, I.
Modelos de propagación electromagnética: Modelos determinísticos de propagación.
[Wagemakers and Borja, b] Wagemakers, A. and Borja, I.
Modelos de propagación electromagnética: Propagación en entorno urbano.
[Wikipedia, 2016a] Wikipedia (2016a).
Inverse-square law.
https://en.wikipedia.org/wiki/Inverse-square_law.
[Online; accessed 09-April-2016].
[Wikipedia, 2016b] Wikipedia (2016b).
Near and far field.
https://en.wikipedia.org/wiki/Near_and_far_field.
[Online; accessed 09-April-2016].
fasandoval@utpl.edu.ec CI CI-Large-Scale Path Loss 68 / 68](https://image.slidesharecdn.com/blargescalepathlossresumen2019-200106134114/85/CI19-2-Presentaciones-Large-scale-path-loss-77-320.jpg)