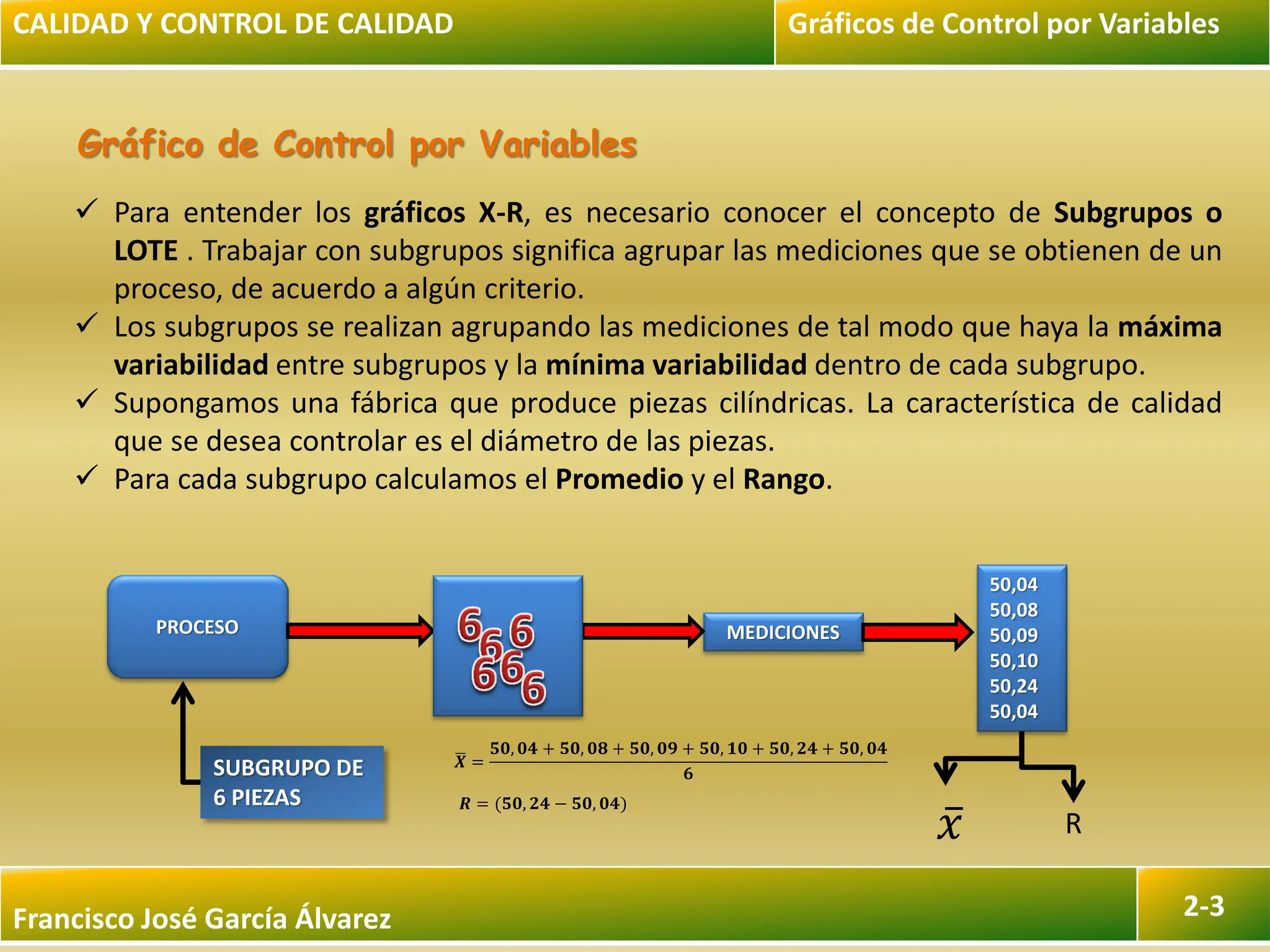
El documento describe los objetivos y procedimientos para la construcción e interpretación de gráficos de control por variables, enfocándose en gráficos X-R y X-S. Se explican conceptos como subgrupos, límites de control, y se establecen las instrucciones prácticas para su uso y análisis de variabilidad en procesos. Además, se abordan índices de capacidad del proceso y su relación con las especificaciones de calidad.