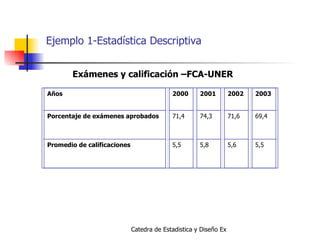
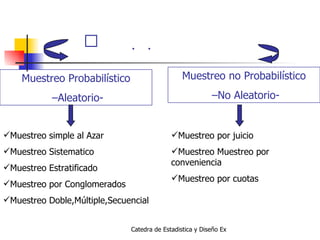
El documento presenta información sobre estadística y diseño experimental. Explica conceptos básicos como población, muestra, variables, estadística descriptiva e inferencial. También describe métodos de muestreo probabilísticos como el muestreo simple aleatorio y no probabilísticos. Finalmente, destaca la importancia de la estadística en la investigación científica.

1. Estadística y Diseño Experimental

2. El pensamiento estadístico algún día será tan necesario , para ser un buen ciudadano , como la habilidad de leer y escribir. H.G. Wells -1903

3. Cuál es el significado de Estadística????

6. . Población total según grupo de edad y sexo Comodoro Rivadavia- Grupos de edad Mujeres Varones Frecuencia % Frecuencia % Hasta 9 años 13590 19.3% 12492 18.1% De 10 a 14 años 7042 10.0% 7454 10.8% De 15 a 19 años 6268 8.9% 5866 8.5% De 20 a 24 años 5775 8.2% 7385 10.7% De 25 a 29 años 5211 7.4% 6557 9.5% De 30 a 39 años 9860 14.0% 8420 12.2% De 40 a 49 años 8099 11.5% 7868 11.4% De 50 a 59 años 7394 10.5% 6764 9.8% De 60 a 69 años 4014 5.7% 3865 5.6% De 70 y mas años 3169 4.5% 2347 3.4% Total 70422 100.0% 69018 100.0%

7. La Estadística se ocupa de los métodos y procedimientos para recoger, clasificar, resumir, hallar regularidades y analizar los datos , siempre y cuando la variabilidad e incertidumbre sea una causa intrínseca de los mismos; así como de realizar inferencias a partir de ellos, con la finalidad de ayudar a la toma de decisiones y en su caso formular predicciones .

8.  Estadística Descriptiva Es la Ciencia que se ocupa de la Recolección y Organización de datos mediante la presentación en Tablas y Gráficos y del Resumen de información numérica mediante el Cálculo de Medidas Descriptivas. Estadística Inferencial Conjunto de métodos que hacen posible la estimación de una característica de la población o la toma de decisión referente a una población, basándose tan sólo en los resultados de la muestra.

9. Ejemplo 1-Estadística Descriptiva Exámenes y calificación –FCA-UNER Años 2000 2001 2002 2003 Porcentaje de exámenes aprobados 71,4 74,3 71,6 69,4 Promedio de calificaciones 5,5 5,8 5,6 5,5

10. Ejemplo 2- Estadística Inferencial Población: mayor de 18 años, en el ámbito geográfico AMBA (Ciudad de Buenos Aires y Gran Buenos Aires). Tamaño de la muestra: 303 Conoce el Programa de Salud Sexual y Procreación Responsable ? ENCUESTA DE OPINIÓN PÚBLICA SOBRE SALUD REPRODUCTIVA - el Ministerio de Salud de la Nación 2003 Aplicando Intervalos de Confianza puede inferirse con un 95% de confianza que entre 21% y 31 % de la población mayor a 18 años del AMBA conoce el Programa Si conoce 26% No conoce 74%

11.   Población Muestra Unidad elemental Observación Variables

12.   

13. Conjunto (universo) de “entidades”, llamadas unidades elementales tales como personas, animales, plantas , establecimientos escolares, avícolas, tamberos..., vehículos...., que posee una característica común observable o medible que define al grupo. Una población se define en tiempo y espacio. Conjunto de observaciones realizadas a todas las unidades elementales “entidades” de la población. Establecimientos Tamberos de Entre Ríos . 200 7 Alumnos ingresantes a la FCA-UNER . 200 8 Alumnos inscriptos a la FCA-UNER. 200 8 Alumnos que cursan Estadística y D. Experimental FCA-UNER.200 8 . 

14.  Grupo de unidades elementales seleccionado mediante un procedimiento científico ( Muestreo ) para representar a la población . Conjunto de observaciones realizadas a las unidades elementales de la muestra .  Es el resultado de observar - clasificar o medir - una característica a las unidades elementales de una muestra o población.

15. Característica, propiedad o atributo , con respecto a la cual los elementos de una muestra o población difieren de un modo verificable.        VARIABLES

16.  Cuantitativas pueden medirse y expresarse en forma numérica Cualitativas son no medibles y se expresan en forma de clases categorías Discretas Continuas Nominales Ordinales

17.   Son aquellas que sólo asumen un número finito de valores ( números enteros). Numero de plantas de trigo / m. de surco Número de chauchas/ planta de soja Número de gallinas/ jaula. Numero de niños desnutridos/ hospital Número de plantas de trigo atacadas/ m2

18. Son aquellas que pueden tomar un número infinito de valores dentro de un intervalo dado .   Temperaturas mínimas diarias en Invierno (°C ) 1 °C  X  5 °C Peso de Niños recién nacidos (Kg) 2 Kg  X  5 Kg Altura de hombres adultos (m) 1.5 mt  X  2mt Volumen de agua caída ( mm 3 ) Rendimiento de un cultivo ( Kg/ha) Area foliar ( cm) Edad ( años/ meses)

19. Son aquellas que si bien no pueden medirse, sus categorías pueden ordenarse en una escala numérica   Calificaciones Sobresaliente :9-10 Distinguido: 8-9 Bueno: 6-7 Aprobado: 4-5 Insuficiente:1-23 Reprobado: 0 Grado de Resistencia al Cancro del Tallo-Soja Resistente: 5 M oderadamente resistente :4 M oderadamente susceptible:3 S usceptible :2 Altamente susceptible :1 Grado de Alcoholismo No bebedor: 0 Bebedor Moderado:1 Bebedor Habitual :3 Bebedor Excesivo:4 Alcoholico: 5

20.   Son aquellas cuyas clases son excluyentes, no pueden medirse ni adoptar una escala ordinal Sexo : Femenino ;Masculino Razas de Ganado Bovino : Shorthorn ; Criolla; Hereford;Aberdeen Angus.. Color de flor: Púrpura; Blanco Forma de Hoja: Ancho; Angosta Nacionalidad :Argentino, Uruguayo, Chileno,.....

21.   Son aquellas basadas en dos o mas variables medidas en forma independiente cuyas relaciones se expresan de determinada forma : Tasas, Razones, Proporciones Índices Kg. aumento de peso/Kg. alimento consumido. Kg., aumento de peso/calorías consumida. Porcentaje de grasa Butirosa de la leche Tasa de Mortalidad Fetal: número de Muertes Fetales / número total de nacidos (vivos + muertos), en un área y año dado. Indices de precios

22.  El rol de la Estadística en la Investigación es el de proveer herramientas útiles para el diseño de experimento, estudios observacionales y relevamientos muestrales . Tipos de Investigación Según Objetivos Análisis Exploratorio Descriptivo Análisis Confirmatorio Inferencial Según Recolección de datos Diseño de Experimentos Estudios Observacionales Relevamientos muestrales

23. Según el modo de recolectar los datos........ Diseños de Experimento: S on diseñados y controlados por el investigador.” Provocan” un fenómeno bajo condiciones controladas . Ej. Aplicación de diferentes dosis de un fertilizante para evaluar el rendimiento de diferentes variedades de trigo. Estudios observacionales S urgen como resultado de un proceso de observación bajo ciertas condiciones dadas . Ej. Datos publicados de registros de temperaturas mínimas y máximas en la ultima década del siglo XX, en la ciudad de Paraná. Relevamientos muestrales S e vinculan con encuestas de opinión aplicando métodos de muestreo para la selección de individuos. Ej. Evaluar la opinión de los estudiantes universitarios respecto a diferentes aspectos del funcionamiento del Departamento Alumnado y Biblioteca de la facultad donde cursan su carrera.

24.  Cuando no es posible medir cada uno de los individuos de una población , se toma una muestra representativa de la misma. Razones que justifican el uso de muestras Población muy grande , potencialmente infinita Dificultades en localizar a todos los elementos de la población Disponibilidad de r ecursos presupuestarios Disponibilidad de r ecursos humanos calificados Destrucción de los elementos al tomar las observaciones. Otos...

25. ... bajo que condiciones, resulta apropiada una muestra? ??? ... qué significa que una muestra sea representativa??? Hacer representativa una muestra tomada en una población supone : que posea un tamaño adecuado que el método de selección -muestreo - utilizado sea el correcto, de manera que todas las unidades de muestreo de la población, estén representadas de forma adecuada. .... qué alcance tiene obtener una muestra representativa??? Poder aplicar métodos de la Estadística Inferencial que permitan extrapolar o tomar decisiones a toda la población, en base a la información obtenida a de la muestra

26. Métodos de muestreos Muestreo no Probabilístico – no aleatorio- Muestreo Probabilístico – Aleatorio- Cada unidad de muestreo tiene la misma posibilidad de ser seleccionada por ende,su probabilidad es conocida Es representativo Es mas costoso El error de muestreo es factible de medir Cada unidad de muestreo se elige por medio de un juicio según opinión del investigador. Carece de representatividad. Es menos costoso El error de muestreo es dificil de evaluar

27.  Muestreo Probabilístico – Aleatorio- Muestreo no Probabilístico – No Aleatorio- Muestreo simple al Azar Muestreo Sistematico Muestreo Estratificado Muestreo por Conglomerados Muestreo Doble,Múltiple,Secuencial Muestreo por juicio Muestreo Muestreo por conveniencia Muestreo por cuotas

28. Muestreo Simple al Azar Cómo se obtiene la muestra????? Se conoce el tamaño N de la Población y las unidades de muestreo están perfectamente identificadas y numeradas Se ha definido el tamaño n de la muestra Todas las unidades de muestreo son escogidas independientemente unas de otras y TODAS las N unidades tienen la siguiente probabilidad de incluidas en la muestra : -1/N ,si el muestreo es con reposición y 1/( N-1), si el muestreo es sin reposición Para la elección de las unidades de muestreo se hace uso de la Tabla de Números Aleatorios

29. Población : N= 30 establecimientos Tamberos en un Departamento Muestra: n=10 Numero del Establecimiento Nombre del Productor 1 BoccaJ.P 2 ........... 3 ........... 4 ........... ................................................................................ 27 ................ 28 ............... 29 ............. 30 Miro, J.S

30. 1 4 1 5 9 2 6 5 3 5 8 9 7 9 3 2 3 8 4 6 2 6 4 3 3 8 3 2 7 9 5 0 2 8 8 4 1 9 7 1 6 9 3 9 9 3 7 5 1 0 5 8 2 0 9 7 4 9 4 4 5 9 2 3 0 7 8 1 6 4 0 6 2 8 6 2 0 8 9 9 8 6 2 8 0 3 4 8 2 5 8 4 2 1 1 7 0 6 7 9 8 2 1 4 8 0 8 6 5 1 3 2 8 2 3 0 6 6 4 7 0 9 3 8 4 4 6 0 9 5 5 0 5 8 2 2 3 1 7 2 5 3 5 9 4 0 8 1 2 8 4 8 1 1 1 7 4 5 0 2 8 4 1 0 2 7 0 1 9 3 8 5 2 1 1 0 5 5 5 9 6 4 4 6 2 2 9 4 8 9 5 4 9 3 0 3 8 1 9 6 4 4 2 8 8 1 0 9 7 5 6 6 5 9 3 3 4 4 6 1 2 8 4 7 5 6 4 8 2 3 3 7 8 6 7 8 3 1 6 5 2 7 1 2 0 1 9 0 9 1 4 5 6 4 8 5 6 6 9 2 3 4 6 0 3 4 8 6 1 0 4 5 4 3 2 6 6 4 8 2 1 3 3 9 3 6 0 7 2 6 0 2 4 9 1 4 1 2 7 3 7 2 4 5 8 7 0 0 6 6 0 6 3 1 5 5 8 8 1 7 4 8 8 1 5 2 0 9 2 0 9 6 2 8 2 9 2 5 4 0 9 1 7 1 5 3 6 4 3 6 7 8 9 2 5 9 0 3 6 0 0 1 1 3 3 0 5 3 0 5 4 8 8 2 0 4 6 6 5 2     Punto de partida Número de serie que integra la muestra