Tema5 Características Generales de las Ondas

Curso2006-2007
UniversidadComplutense 1/351/35
Tema 5
Características generales de las ondas

Curso2006-2007
Cuerda con cuentas
Cuerda elástica de masa despreciable sometida a una tensión T0 en el equi-
librio con N masas m separadas por una distancia l.
l =
l
cos αi−1
l 1 + O(α2
i−1)
Empleando la ley de Hooke
T T0

Curso2006-2007
Fuerza paralela que actúa sobre la partícula i
T0 cos αi − T0 cos αi−1
T0
2
α2
i−1 − α2
i → 0
mientras que la componente perpendicular es
mÿi = T0 sen αi − T0 sen αi−1 T0 tan αi − T0 tan αi−1
Definiendo ω2
0 ≡ T0/ml obtenemos
ÿi + ω2
0 (2yi − yi+1 − yi−1) = 0 y0 = yN+1 = 0

Curso2006-2007
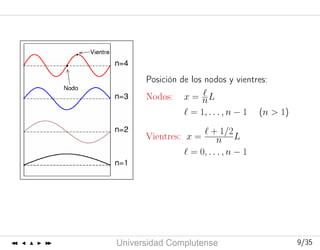
Determinación de los modos normales
yi(t) = Ai cos ωt con A0 = AN+1 = 0.
2ω2
0 − ω2
Ai − ω2
0 (Ai+1 + Ai−1) = 0 i = 1, 2, . . . N
Usando como solución Ai = B sen(iθ)
cos θ =
2ω2
0 − ω2
2ω2
0
Las condiciones de contorno se cumplen si
sen [(N + 1)θ] = 0 =⇒ ωn = 2ω0 sen
nπ
2(N + 1)
n = entero

Curso2006-2007
ωn y −ωn son físicamente equivalentes: n ≥ 0.
n = 0 es un modo de traslación: n > 0.
n = N + 1 implica θ = π y Ai = 0.
ωN+2 = ωN ωN+3 = ωN−1 . . . ω2N+1 = ω1.
Por tanto, los modos normales son
yin(t) = B sen
inπ
N + 1
cos ωnt i, n = 1, 2, . . . , N

Curso2006-2007
Límite contínuo
N → ∞, l → 0, m → 0 con L ≡ (N + 1)l = cte y M ≡ mN = cte.
Las frecuencias más bajas veriﬁcan que
ωn ω0
nπ
N + 1
=
nπ
L
T0
µ
= nω1 ω1 =
π
L
T0
µ
yn(x, t) = B sen
nπx
L
cos(nω1t) n = 1, 2, . . .
Solución general
ψ(x, t) =
∞
n=1
Bn sen(κnx) cos(ωnt + δn)

Curso2006-2007
Ondas en una cuerda vibrante
|T1| |T2| T0
Segunda ley de Newton
µ∆x
∂2
ψ
∂t2
T0
∂ψ
∂x x+∆x
− T0
∂ψ
∂x x
T0∆x
∂2
ψ
∂x2
Deﬁniendo v ≡ T0/µ obtenemos la ecuación de ondas
1
v2
∂2
ψ
∂t2
=
∂2
ψ
∂x2

Curso2006-2007
Modos normales.
Condiciones de contorno ψ(0, t) = ψ(L, t) = 0. Onda estacionaria.
ψ(x, t) = A(x) cos(ωt + δ) =⇒ A (x) + κ2
A(x) = 0
donde se cumple la relación de dispersión para la cuerda
ω = κv
La solución buscada es A(x) = α sen κx + β cos κx. A(0) = 0 =⇒ β = 0
y A(L) = 0 =⇒ κL = nπ. Los modos normales son
ψn(x, t) = α sen
nπx
L
cos
nπvt
L
+ δ n = 1, 2, . . .

Curso2006-2007
Posición de los nodos y vientres:
Nodos: x = nL
= 1, . . . , n − 1 (n > 1)
Vientres: x =
+ 1/2
n L
= 0, . . . , n − 1

Curso2006-2007
Solución general de la ecuación de ondas
Las soluciones son ondas viajeras (so-
lución de d’Alembert)
ψ(x, t) = f(x − vt) + g(x + vt)
El signo − indica propagación en la direc-
ción positiva del eje X y el signo + en la
negativa.
La forma de la onda NO cambia en el tiempo.

Curso2006-2007
Para demostralo deﬁnimos la variable u ≡ x − vt y aplicamos la regla de
la cadena:
∂ψ
∂x
=
∂u
∂x
df
du
=
df
du
∂2
ψ
∂x2
=
∂
∂x
df
du
=
∂u
∂x
d2
f
du2
=
d2
f
du2
∂ψ
∂t
= −v
∂u
∂u
df
du
= −v
df
du
∂2
ψ
∂t2
= −v
∂
∂t
df
du
= −v
∂u
∂t
d2
f
du2
= v2 d2
f
du2
= v2 ∂2
ψ
∂x2
De la misma manera se puede mostrar que g(x + vt) también es solución
de la ecuación de ondas.

Curso2006-2007
Si una onda viajera es periódica en el espacio, también lo es en el tiempo,
y viceversa.
Sea ψ(x, t) = ψ(x, t + T) periódica en el tiempo, con período T. Entonces
ψ(x, t) = f(x ± vt) = ψ(x, t + T) = f(x ± vt ± vT) = ψ(x ± vT, t)
por lo que es periódica en el espacio, con período vT.
Principio de superposición
Cuando dos o más ondas se encuentran en el mismo lugar del espacio en el
mismo tiempo se dice que interﬁeren. La función de onda resultante es la
suma de todas ellas.
Para visualizar una animación pinche sobre la imagen:

Curso2006-2007
Ondas monocromáticas
Es un caso particular de onda viajera
ψ(x, t) = ψ0 sen[κ(x ± vt) + δ] = ψ0 sen[κx ± ωt + δ]
ψ(x, t) = A sen[κx ± ωt] + B cos[κx ± ωt]
ψ(x, t) = Re {D exp[i(κx ± ωt)]}
Longitud de onda λ = 2π/κ período T = 2π/ω
El movimiento que realiza cada punto es armónico simple, cuya fase depende
del punto considerado.
ψ(x0, t) = ψ0 sen[κx0 ± ωt + δ] = ψ0 sen[ωt + φ(x0)]

Curso2006-2007
Velocidad de fase
Se deﬁne la fase de la onda sinusoidal como
ϕ(x, t) = κx − ωt
La velocidad vo a la que debe moverse un observador para que la fase sea
estacionaria
dϕ
dt
= κ
dx
dt
vo
−ω
e imponiendo la condición de que
dϕ
dt
= 0 obtenemos que vo = v. Habi-
tualmente v recibe el nombre de velocidad de fase

Curso2006-2007
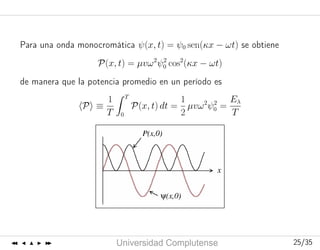
Superposición de ondas monocromáticas
Misma frecuencia y amplitud pero direcciones opuestas.
ψ1(x, t) =
ψ0
2
sen(κx − ωt) ψ2(x, t) =
ψ0
2
sen(κx + ωt)
ψ(x, t) = ψ1(x, t) + ψ2(x, t) = ψ0 sen κx cos ωt
Para visualizar la onda estacionaria, pinche sobre el icono:
Pulsaciones.
ψ1(x, t) =
ψ0
2
sen[κ1(x − vt)] ψ2(x, t) =
ψ0
2
sen[κ2(x − vt)]
ψ(x, t) = ψ0 sen
κ1 + κ2
2
(x − vt) cos
κ1 − κ2
2
(x − vt)
onda moduladora

Curso2006-2007
En el instante t = 0 tendremos
ψ(x, t = 0) = ψ0 sen 2π
x
λ−
cos 2π
x
λ+
λ± ≡
4π
|κ1 κ2|

Curso2006-2007
Reﬂexión y transmisión en cuerdas
Para generar una onda monocromática en
una cuerda basta hacer que un extremo se
mueva con movimiento armónico simple
con la frecuencia y amplitud deseadas.

Curso2006-2007
La tensión que la cuerda ejerce sobre el punto de sujección es T0
∂ψ
∂x x=0
por lo que la fuerza que debe ejercer el motor es
FM→C = −T0
∂ψ
∂x x=0
=
T0
v
∂ψ
∂t x=0
= T0µ
∂ψ
∂t x=0
donde la impedancia característica es Z0 ≡ T0µ
Condiciones de contorno en una discontinuidad
La fuerza neta sobre el nudo es
(Z1 − Z2)
∂ψ
∂t x=0
= 0
si Z1 = Z2. Si la masa del nudo es des-
preciable, tendría aceleración inﬁnita.

Curso2006-2007
La alternativa es admitir que existe
una onda reﬂejada, de manera que
pueda cumplirse que la fuerza neta so-
bre el nudo sea nula.
ψi(0, t) + ψr(0, t) = ψt(0, t)
T1
∂ψi
∂x x=0
+ T1
∂ψr
∂x x=0
− T2
∂ψt
∂x x=0
= 0 =⇒
Z1
∂ψi
∂t x=0
−
∂ψr
∂t x=0
= Z2
∂ψt
∂t x=0

Curso2006-2007
Empleando la continuidad de la función de onda
(Z1 − Z2)
∂ψi
∂t x=0
= (Z1 + Z2)
∂ψr
∂t x=0
e integrando respecto al tiempo
ψr(0, t) = Rψi(0, t)
donde se ha definido el coeficiente de reflexión como
R =
Z1 − Z2
Z1 + Z2
, −1 ≤ R ≤ +1
Extremo libre: Z2 = 0 =⇒ R = 1. Pinche sobre el icono:
Extremo fijo: Z2 → ∞ =⇒ R = −1. Pinche sobre el icono:

Curso2006-2007
Como ψt(0, t) = ψi(0, t) + ψr(0, t) y ψr(0, t) = Rψi(0, t) resulta que
ψt(0, t) = Tψi(0, t)
donde se ha deﬁnido el coeﬁciente de transmisión como
T = 1 + R =
2Z1
Z1 + Z2
, 0 < T < 2
Si ambas tensiones son iguales podemos obtener que
R =
v2 − v1
v2 + v1
T =
2v2
v2 + v1
Pinche sobre el icono para ver qué ocurre cuando Z1 < Z2:
Pinche sobre el icono para ver qué ocurre cuando Z1 > Z2:

Curso2006-2007
Energía propagada en la cuerda
ds−dx = dx2
+ dψ2 1/2
−dx =

 1 +
∂ψ
∂x
2
− 1

 dx
1
2
∂ψ
∂x
2
dx
por lo que la variación de energía potencial es
dEp =
1
2
T0
∂ψ
∂x
2
dx

Curso2006-2007
La energía cinética es
dEc =
1
2
µ
∂ψ
∂t
2
dx
por lo que la densidad de energía es
dE
dx
=
1
2
µ
∂ψ
∂t
2
+
1
2
T0
∂ψ
∂x
2
Para una onda monocromática ψ(x, t) = ψ0 sen(κx − ωt) se obtiene
dE
dx
= µω2
ψ2
0 cos2
(κx − ωt)
y la energía para que vibre un segmento de longitud λ es
Eλ =
λ
0
dE
dx
dx =
1
2
µλω2
ψ2
0

Curso2006-2007
Potencia propagada en la cuerda
La energía almacenada entre x − dx y x en un instante t pasa a estar entre
x y x + dx en el instante t + dt con dt = dx/v.
Por tanto
P(x, t) =
dE
dt
= v
dE
dx
P(x, t) =
v
2
µ
∂ψ
∂t
2
+
v
2
T0
∂ψ
∂x
2

Curso2006-2007
Para una onda monocromática ψ(x, t) = ψ0 sen(κx − ωt) se obtiene
P(x, t) = µvω2
ψ2
0 cos2
(κx − ωt)
de manera que la potencia promedio en un período es
P ≡
1
T
T
0
P(x, t) dt =
1
2
µvω2
ψ2
0 =
Eλ
T

Curso2006-2007
Atenuación
Cuando sumergimos la cuerda en un ﬂuido aparece una fuerza de fricción
que es proporcional a la velocidad de cada segmento.
µ
∂2
ψ
∂t2
= T0
∂2
ψ
∂x2
− β
∂ψ
∂t
=⇒
∂2
ψ
∂t2
+ Γ
∂ψ
∂t
= v2 ∂2
ψ
∂x2
Γ ≡
β
µ
ψ(x, t) = ψ0 exp[i(Υx − ωt)] Υ ≡ κ + iγ
Sustituyendo en la ecuación de ondas ω2
+ iΓω = v2
Υ2
ω2
= v2
κ2
− γ2
Γω = 2v2
κγ
ψ(x, t) = ψ0e−γx
exp[i(κx − ωt)] 1/γ: longitud de atenuación

Curso2006-2007
Débil: Γ/ω 1.
v(κ + iγ) = ω 1 + iΓ/ω ω + iΓ/2,
ω = κv γ =
Γ
2v
λ γ−1
Fuerte: Γ/ω 1.
v2
(κ + iγ)2
= ω2
+ iΓω iΓω,
κ γ
Γω
2v2
Γω = 2γκv2
λ ∼ γ−1

Curso2006-2007
Impedancia característica en presencia de atenuación
La fuerza transversal que debemos realizar sobre la cuerda es
−T0
∂ψ
∂x
= −Re iΥT0ψ0ei(Υx−ωt)
= Re
ΥT0
ω
∂ψ
∂t
por lo que podemos deﬁnir una impedancia compleja
Z0 =
T0Υ
ω
=
T0
ω
(κ + iγ)
Atenuación débil: Z0 T0µ (1 + iΓ/2ω)
Atenuación fuerte: Z0 T0µ (1 + i) Γ/2ω.

Curso2006-2007
Discontinuidad
Consideremos una onda sobre una cuerda que pasa de una región donde no
hay atenuación, con impedancia característica Z1 =
√
T0µ, a otro medio
donde hay atenuación, con impedancia característica Z2. En los dos casos
límites considerados, el coeﬁciente de reﬂexión R = (Z1 − Z2)/(Z1 + Z2)
es
Débil:
R −i
Γ
4ω
|R| 1
Fuerte:
R −1 (Pared rigida)

Curso2006-2007
Velocidad de grupo
ψ1(x, t) =
ψ0
2
sen[(κ − dκ)x − (ω − dω)t]
ψ2(x, t) =
ψ0
2
sen[(κ + dκ)x − (ω + dω)t]
Pulsación:
ψ(x, t) = ψ0 cos (dκ x − dω t)
Moduladora
sen(κx − ωt)

Curso2006-2007
La velocidad de la onda moduladora recibe el nombre de velocidad de
grupo. Representa la velocidad a la que se debe mover un observador para
que determine que la amplitud de la onda no cambia.
vg ≡
dω
dκ
= v + κ
dv
dκ
En los medios no dispersivos las velocidades de fase y de grupo coinciden
(v no depende de κ). En los medios dispersivos cada onda monocromática
viaja a una velocidad diferente. La superposición de ellas (típicamente un
paquete de ondas) cambia de forma en el transcurso del tiempo.
Relación de dispersión: ω = ω(κ)
Pinche sobre el icono para ver qué sucede en un medio dispersivo:

Curso2006-2007
Paquetes de onda gaussianos
ψ(x, t) =
∞
−∞
C(κ)ei(κx−ωt)
dκ C(κ) = Ae−σ2(κ−κ0)2
ψ(x, 0) = A
∞
−∞
eiκx−σ2(κ−κ0)2
dκ
= A
√
π
σ
eiκ0x
e−x2/4σ2

Curso2006-2007
ω(κ) = ω(κ0) +
dω
dκ κ0
(κ − κ0) +
1
2
d2
ω
dκ2
κ0
(κ − κ0)2
+ · · ·
≡ ω0 + vg(κ0)(κ − κ0) + β(κ0)(κ − κ0)2
, β(κ) ≡
1
2
dvg
dκ
En los medios no dispersivos β(κ) = 0, por lo que
ψ(x, t) =
∞
−∞
C(κ)ei[κx−ω0t−vg(κ0)(κ−κ0)t]
dκ
Teniendo en cuenta que en este caso vg(κ0) = v y que ω0 = vκ0 resulta
ψ(x, t) =
∞
−∞
C(κ)eiκ(x−vt)
dκ = ψ(x − vt, 0)
es decir, el paquete gaussiano se propaga sin distorsión. Debemos notar que
no se ha hecho uso de la forma explícita de C(κ), por lo que esta conclusión
es válida para la dinámica de cualquier pulso en medios no dispersivos.

Curso2006-2007
En los medios dispersivos β(κ) = 0, por lo que
ψ(x, t) =
∞
−∞
C(κ)e−iβ(κ0)(κ−κ0)2t
ei[κ(x−vg(κ0)t)+φ(κ0,t)]
dκ
donde φ(κ0, t) ≡ ω0t[1 − vg(κ0)/v(κ0)], siendo v(κ0) = ω0/κ0 la velocidad
de fase. Además de esta fase φ(κ0, t), la presencia de un término cuadrático
en la relación de dispersión origina el factor exp{−iβ(κ0)(κ − κ0)2
t} en el
integrando. En consecuencia, en el medio dispersivo hemos de reemplazar σ
por σ+iβ(κ0)t. Así obtenemos que la envolvente sigue siendo una gaussiana,
pero su anchura crece en el tiempo pues
σ(t) = σ 1 + β2(κ0)t2

Curso2006-2007
Ondas en medios no homogéneos: Método WBK.
v(x) lentamente variable en el espacio.
1
v2(x)
∂2
ψ
∂t2
=
∂2
ψ
∂x2
ψ(x, t) = A(x)ei[f(x)−ωt]
donde A(x) y f(x) son funciones reales. Sustituyendo la solución propuesta
en la ecuación y despreciando A (x) obtenemos dos ecuaciones
f (x) =
ω
v(x)
=⇒ f(x) = ω
x
x0
dy
v(y)
2 A (x)f (x) + Af (x) = 0 =⇒
A(x)
A(x0)
=
f (x0)
f (x)
=
v(x)
v(x0)
ψ(x, t) = A(x0)
v(x)
v(x0)
exp iω
x
x0
dy
v(y)
− t

Tema5 Características Generales de las Ondas

Más contenido relacionado

La actualidad más candente

Similar a Tema5 Características Generales de las Ondas

Más de rafarrc

Tema5 Características Generales de las Ondas