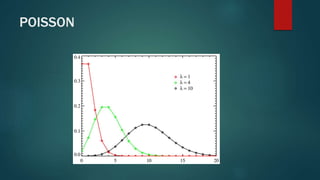
El documento resume los principales temas de estadística tratados en un curso, incluyendo variables aleatorias, función de probabilidad, densidad, distribuciones como la de Bernoulli, binomial y Poisson, y tipificación. Explica conceptos como la probabilidad asociada a cada punto de una variable aleatoria, la densidad como probabilidad relativa de un valor, y las distribuciones que cuentan el número de éxitos en ensayos independientes.

1. TEMAS DEL PARCIAL
ESTADÍSTICA

2. INTRODUCCIÓN
 En estas diapositivas observaremos y leeremos
los que aprendimos en este periodo
escolarizado. En estos temas que podrán leer,
vienen algunos temas que podrás comprender
con la lectura .
 En la asignatura de estadística vimos los temas:
variables aleatorias, función de probabilidad,
función de densidad, distribución , ect..

3. VARIABLES ALEATORIA
 El resultado de un experimento aleatorio puede
ser descurto en ocasiones como una cantidad
numérica .
en estos casos encontramos variables
aleatorias , función de asigna a cada suceso un
numero.
Las variables aleatorias pueden ser discretas o
contenías ( como en el primer del curso).

4. FUNCIÓN DE PROBABILIDAD
 En teoría de la probabilidad, una función de probabilidad
(también denominada función de masa de probabilidad)
es una función que asocia a cada punto de su espacio
maestral X la probabilidad de que ésta lo asuma.
p(x1)=pi
 donde pi es la probabilidad del suceso X = xi.
Por definición de probabilidad

5. DENSIDAD
 En la función de densidad, o, simplemente, densidad de
una variable aleatoria continua describe la probabilidad
relativa según la cual dicha variable aleatoria tomará
determinado valor.
La probabilidad de que la variable aleatoria caiga en
una región específica del espacio de posibilidades estará
dada por la integral de la densidad de esta variable entre
uno y otro límite de dicha región.

6. DENSIDAD
IMAGEN

7.  En la teoría de la probabilidad y en estadística,
una función de distribución acumulada describe
la probabilidad de que una variable aleatoria
real X sujeta a cierta ley de distribución de
probabilidad se sitúe en la zona de valores
menores o iguales a x.

8.  Intuitivamente, asumiendo la función f como la
ley de distribución de probabilidad, la sería la
función con la recta real como dominio, con
imagen del área hasta aquí de la función f,
siendo aquí el valor x para la variable aleatoria
real X.

10. DISTRIBUCION DE BERNOULIN
 la distribución de Bernoulli (o distribución
dicotómica), nombrada así por el matemático y
científico suizo Jakob Bernoulli, es una
distribución de probabilidad discreta, que toma
valor.

11.  Si X es una variable aleatoria que mide el
"número de éxitos", y se realiza un único
experimento con dos posibles resultados (éxito
o fracaso), se dice que la variable
aleatoria X se distribuye como una Bernoulli de
parámetro P .

12. DISTRIBUCION BINOMIAL
 la distribución binomial es una distribución de
probabilidad discreta que cuenta el número de
éxitos en una secuencia de n ensayos de
Bernoulli independientes entre sí, con una
probabilidad fija p de ocurrencia del éxito entre
los ensayos. Un experimento de Bernoulli se
caracteriza por ser dicotómico, esto es, sólo son
posibles dos resultados

13.  A uno de estos se denomina éxito y tiene una
probabilidad de ocurrencia p y al otro, fracaso,
con una probabilidad q = 1 - p. En la distribución
binomial el anterior experimento se repite n
veces, de forma independiente, y se trata de
calcular la probabilidad de un determinado
número de éxitos. Para n = 1, la binomial se
convierte, de hecho, en una distribución de
Bernoulli.

14. DISTRIBUCION DE POISSON
 La distribución de Poisson es una distribución
de probabilidad discreta que expresa, a partir de
una frecuencia de ocurrencia media, la
probabilidad de que ocurra un determinado
número de eventos durante cierto período de
tiempo. Concretamente, se especializa en la
probabilidad de ocurrencia de sucesos con
probabilidades muy pequeñas, o sucesos
"raros".

15. POISSON

16. TIPIFICACION
 De cada variable de media y desviación típica,
se denomina valor tipificado, de una
observación de x , ala distancia con respeto ala
media, medido en desviación típica, es decir
Z= X - μ
δ

17. En el caso de variables X normal, la interpretación
es clara; asigna a todos los valores en N(μ . δ ) un
valor de N(0,1) que deja exactamente la misma
probabilidad por de bajo.