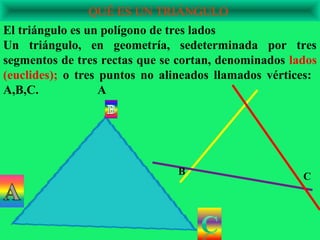
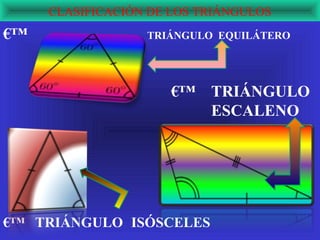
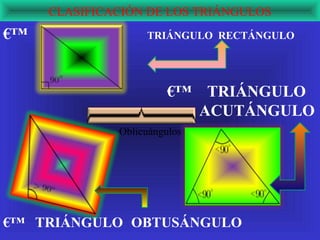
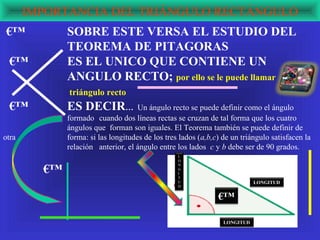
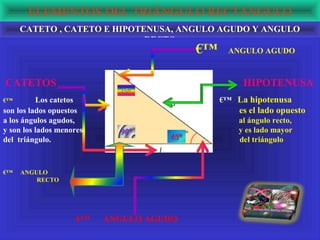
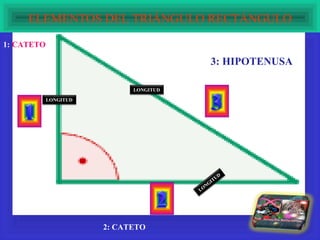
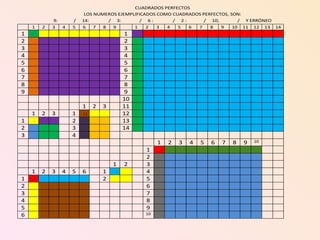
El documento explora la relación de la tecnología con las matemáticas, centrándose en el teorema de Pitágoras y la clasificación de los triángulos. Se abordan conceptos clave como los tipos de triángulos, la definición de teorema y la importancia del triángulo rectángulo en la aplicación del teorema. Además, se incluye un ejemplo matemático que demuestra la relación entre los lados de un triángulo rectángulo usando potencias y raíces cuadradas.

1. ENRIQUE
TORRESCANO
MONTIEL
URA
NAT GÍA
ASIG LO
TE CNO

2. RELACION DE LA
TECNOLOGIA CON
OTRAS AREAS DEL
CONOCIMIENTO
DE
MA ”
RE AS
“ TEO GOR
PIT Á

3. LOS CONOCIMIENTOS PREVIOS Y/O POR ADQUIRIR
PARA EL DESARROLLO DE ESTA ACTIVIDAD, SE
NECESITA:
€™ TENER UN CONOCIMIENTO MATEMÁTICO
€™ MANEJAR CONTENIDOS SOBRE TRIÁNGULOS; GEOMETRIA
€™ HABILIDADES EN EL MANEJO DE ESCUADRAS,
TRANSPORTADOR, COMPÁS, CALCULADORA BÁSICA
€™ SISTEMAS MATEMÁTICOS:
€™ ALGEBRA,
€™ GEOMETRÍA,
€™ RAÍZ CUADRADA,
€™ NUMEROS ELEVADOS AL CUADRADO,
€™ POTENCIAS,
€™ RAZONAMIENTO MATEMÁTICO; IMAGINACION ESPACIAL,
€™ SUMA, RESTA, DIVISIÓN, MULTIPLICACIÓN

4. EL TEOREMA DE PITÁGORAS
El Teorema de Pitágoras
Establece que
en un triángulo rectángulo,
el cuadrado de la hipotenusa es igual
a la suma de los cuadrados de los catetos.
Qué es un Teorema
Un teorema es la afirmación que puede ser demostrada como verdadera
dentro de un marco lógico.
Expresar teoremas es un asunto central en el desarrollo de las matemáticas.
Un teorema generalmente posee un número de condiciones que deben ser
enumeradas o aclaradas de antemano y que se denominan respuesta,
Luego existe una conclusión, una afirmación matemática, la cual es verdadera
bajo las condiciones en las que se trabaja.

5. POR QUIÉN RECIBE EL NOMBRE DE…
Por Pitágoras de Samos
Fue un filósofo
y matemático griego, famoso por el Teorema de Pitágoras,
que en realidad perteneció a la escuela pitagórica y no tan
sólo al mismo matemático que nos ocupa.
Nació: alrededor del 569 a. C en Samos, Jonia
Murió: sobre el 475 a.C.
Pitágoras de Samos es descrito a menudo como el primer
matemático puro, es una figura importante en el desarrollo
de las matemáticas aunque

6. SOBRE QUÉ TRABAJA EL TEOREMA DE PITÁGORAS
Sobre los triángulos, entiéndase
cualquier tipo de triángulo.
Haciendo la aclaración de que no
se aplica la misma fórmula para
cada tipo de triángulo.
En nuestro caso nos ocuparemos
de los triángulos rectángulos.
Para triángulos no rectángulos, se aplica la fórmula generalizada de
Pitágoras, siendo más complejo su desarrollo matemático.

7. QUÉ ES UN TRIÁNGULO
El triángulo es un polígono de tres lados
Un triángulo, en geometría, sedeterminada por tres
segmentos de tres rectas que se cortan, denominados lados
(euclides); o tres puntos no alineados llamados vértices:
A,B,C. A
B C

8. Y POR QUÉ EL NOMBRE EUCLIDES
DADO A LOS LADOS DE LOS TRIÁNGULOS
Euclides (en griego Ευκλείδης,
Eukleides) fue un matemático y
geómetra griego, que vivió alrededor
del año 300 a.C., ~ (325 a. C.) - (265 a. C.).
Se le conoce como "El Padre de la
Geometría".

9. QUÉ ES UN POLIGONO
La palabra polígono proviene del griego antiguo (polygōnon),
de poli, "muchos" y gonos, "ángulo".
Un polígono es una figura geométrica conformada por segmentos consecutivos no
alineados, reciben el nombre de lados.

10. CLASIFICACIÓN DE LOS TRIÁNGULOS
€™ EXISTEN TRES TIPOS DE TRIÁNGULOS
€™ Los triángulos se clasifican por la longitud
de sus lados o por la amplitud de sus ángulos.
€™ Por la longitud de sus lados, los
triángulos se clasifican en:
Triángulo equilátero: Tres lados tienen la misma longitud (los tres
ángulos internos miden 60 grados ó radianes.)
Triángulo isósceles: Tiene dos lados de la misma longitud. Los
ángulos que se oponen a estos lados tienen la misma medida.
Triángulo escaleno: Considerado así si todos sus lados tienen
longitudes diferentes.

11. CLASIFICACIÓN DE LOS TRIÁNGULOS
€™ TRIÁNGULO EQUILÁTERO
€™ TRIÁNGULO
ESCALENO
€™ TRIÁNGULO ISÓSCELES

12. CLASIFICACIÓN DE LOS TRIÁNGULOS
€™ por la amplitud de sus ángulos.
€™ Por la amplitud de sus ángulos, los triángulos se
clasifican en:
Triángulo rectángulo: si tiene un ángulo interior recto
(90°). A los dos lados que conforman el ángulo recto se
les denomina catetos y al otro lado hipotenusa.
Triángulo obtusángulo: si uno de sus ángulos es obtuso
(mayor de 90°); los otros dos son agudos (menor de
90°).
Triángulo acutángulo: cuando sus tres ángulos son
menores a 90°; el triángulo equilátero es un caso
particular de triángulo acutángulo.

13. CLASIFICACIÓN DE LOS TRIÁNGULOS
€™ TRIÁNGULO RECTÁNGULO
€™ TRIÁNGULO
ACUTÁNGULO
Oblicuángulos
€™ TRIÁNGULO OBTUSÁNGULO

14. IMPORTANCIA DEL TRIÁNGULO RECTÁNGULO
€™ SOBRE ESTE VERSA EL ESTUDIO DEL
TEOREMA DE PITAGORAS
€™ ES EL UNICO QUE CONTIENE UN
ANGULO RECTO; por ello se le puede llamar
triángulo recto
€™ ES DECIR… Un ángulo recto se puede definir como el ángulo
formado cuando dos líneas rectas se cruzan de tal forma que los cuatro
ángulos que forman son iguales. El Teorema también se puede definir de
otra forma: si las longitudes de los tres lados (a,b,c) de un triángulo satisfacen la
relación anterior, el ángulo entre los lados c y b debe ser de 90 grados.
L
O
€™
N
G
I
T
U LONGITUD
D
€™
LONGITUD

15. NUESTRO CASO: EL TRIÁNGULO RECTANGULO
El triángulo rectángulo / ( recto ) tiene un
ángulo de 90 grados y dos de 45°. Y ya que
la suma de los tres ángulos de un triángulo
suman 180 grados (para cualquier triángulo), se puede
deducir que los otros dos ángulos miden cada uno menos
de 90 grados. A estos ángulos se les llama agudos y
complementarios (su suma es de 90 grados).
SI SUMAS: (en este ejemplo)
90° + 45° + 45° €™
EL RESULTADO ES: 180 grados y
Por ello la suma de todos los ángulos
Internos de un triángulo, siempre
Será de 180 grados, no importando
El tipo de triángulo que sea.

16. ELEMENTOS DEL TRIÁNGULO RECTÁNGULO
CATETO , CATETO E HIPOTENUSA, ANGULO AGUDO Y ANGULO
RECTO
€™ ANGULO AGUDO
CATETOS HIPOTENUSA
€™ Los catetos €™ La hipotenusa
son los lados opuestos es el lado opuesto
a los ángulos agudos, al ángulo recto,
y son los lados menores y es lado mayor
del triángulo. del triángulo
€™ ANGULO
RECTO
€™ ANGULO AGUDO

17. ELEMENTOS DEL TRIÁNGULO RECTÁNGULO
1: CATETO
3: HIPOTENUSA
LONGITUD
LONGITUD
UD
IT
NG
LO
2: CATETO

18. ELEMENTOS DEL TRIÁNGULO RECTÁNGULO P ARA PODER
HACER USO DE LAS MATEMATICAS
AHORA: SI LOS VERTICES DE UN
TRIÁNGULO SON A,B,C, EN LETRAS
MAYÚSCULAS ( No importando su orden )
Los lados del triángulo, son llamados, como
todos los segmentos, por sus extremos:
AB, BC y AC, en nuestro ejemplo.
CÓMO DISTINGUIR la longitud de SUS LADOS:
a PARA BC b PARA AC c PARA AB
SI TE FIJAS, AHORA APARECE LA LETRA minúscula en BC / AC / AB
POR ELLO EL LADO AB PUEDE MEDIR “ n ” LONGITUD Y SE LE CONOCE COMO c
POR ELLO EL LADO BC PUEDE MEDIR “ n ” LONGITUD Y SE LE CONOCE COMO a
POR ELLO EL LADO AC PUEDE MEDIR “ n ” LONGITUD Y SE LE CONOCE COMO b
Para nombrar la longitud de un lado, por lo general se utiliza el nombre del vértice
opuesto, convertido a minúscula latina
EL LADO c ES UN CATETO
EL LADO a ES UN CATETO
EL LADO b ES LA HIPOTENUSA

19. EL TRIÁNGULO Y LAS MATEMÁTICAS
EN UN TRIÁNGULO RECTÁNGULO SE UTILIZA EL TEOREMA DE
PITÁGORAS Y ESTE DICE QUE:
EN UN TRIÁNGULO RECTÁNGULO, EL CUADRADO DE LA HIPOTENUSA
ES IGUAL A LA SUMA DE LOS CUADRADOS DE LOS CATETOS.
ENTONCES LOS VALORES SON: a, b, c.
EN ESTE PRIMER EJEMPLO TENDREMOS
COMO INCOGNITA A: c, QUE ES LA HIPOTENUSA
Y COMO DICE EL TEOREMA, LA HIPOTENUSA ES EL
RESULTADO DE LA SUMA DE LOS CUADRADOS
DE LOS CATETOS
Y DEBEMOS ENTENDER QUE ENTONCES VAMOS A APLICAR
UNA POTENCIACION SOBRE LOS CATETOS, YA QUE EL TEOREMA DICE:
LA SUMA DE LOS CUADRADO DE LOS CATETOS.
EN MATEMATICAS SE DICE ASÍ: a + b = c 2 2 2
EN ESTE SENTIDO HABREMOS DE COMPRENDER QUE USAREMOS EL CONCEPTO DE NUMERO
ELEVADO AL CUADRADO Y UNA RAIZ CUADRADA COMO MEDIO DE SOLUCION A NUESTRO
PROBLEMA

20. COLOQUEMOS UN VALOR NUMÉRICO
ENTONCES LOS VALORES SON: 15,20, incógnita.
EN MATEMATICAS SE DICE ASÍ: a2 + b2 = c2
BIEN, DEBEMOS EXPRESARLE ASÍ
a2 + b 2 = c 2
a es igual a 20 n
b es igual a 15 n
C ES LA INCOGNITA
PERO RECORDEMOS QUE es al cuadrado Y, entonces:
(a) (a), es igual a 202 (20 al cuadrado), ES IGUAL A 20 . 20
(b) (b), es igual a 152 (15 al cuadrado), ES IGUAL A 15 . 15
Entonces: 20.20 = 400 n Y 15.15 n = 225 n
Se suman los valores obtenidos: 400 n + 225 n = 625 n
Sobre el valor obtenido 625 n, se aplica una raíz cuadrada:
√ 625 n el valor de c es, entonces: 25 n
Comprobemos 25 x 25 = 625 y cerramos: en un ángulo con catetos conocidos con
15 y 20 n. El valor de la hipotenusa, usando el Teorema de Pitágoras, es de 25 n.

21. POTENCIACION
Potencia
Potencia: Es el número de veces en que debe multiplicarse la base
por si misma, según su exponente.
La potenciación es una expresión matemática que incluye dos términos
denominados: base a y exponente n.
Se escribe an, y se lee: “a elevado a n”. La definición varía según el conjunto
numérico al que pertenezca el exponente
BASE
a n
12 3
EXPONENTE

22. PRACTIQUEMOS MATEMATICAS
€™ NÚMERO CUADRADO PERFECTO
ES EL NUMERO QUE MULTIPLICADO POR SI MISMO,
RESULTA EN “x” CANTIDAD.
EJEMPLO : n 2
ó BIEN: 102
EL RESULTADO DE ELEVAR AL CUADRADO EL
NUMERO, ES:
10 x 10 = 100
OTRO EJEMPLO;

23. CUADRADOS PERFECTOS
LOS NUMEROS EJEMPLIFICADOS COMO CUADRADOS PERFECTOS, SON:
9: / 14: / 3: / 6: / 2: / 10; / Y ERRÓNEO
1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 10 11 12 13 14
1 1
2 2
3 3
4 4
5 5
6 6
7 7
8 8
9 9
10
1 2 3 11
1 2 3 1 12
1 2 13
2 3 14
3 4
1 2 3 4 5 6 7 8 9 10
1
2
1 2 3
1 2 3 4 5 6 1 4
1 2 5
2 6
3 7
4 8
5 9
6 10

24. Enrique Torrescano
Montiel
E.S.T.I.C 56
“José Antonio Torres”