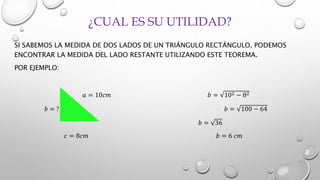
El documento presenta información sobre el teorema de Pitágoras. Explica que Pitágoras fue un filósofo y matemático griego que hizo contribuciones importantes a las matemáticas. Luego enuncia el teorema de Pitágoras, que establece que en cualquier triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. Finalmente, menciona algunas aplicaciones del teorema para resolver problemas geométricos y de distancia.

1. TEOREMA DE
PITÁGORAS

2. ¿QUIEN FUE PITÁGORAS?
PITÁGORAS DE SAMOS FUE UN FILÓSOFO Y MATEMÁTICO GRIEGO
CONSIDERADO EL PRIMER MATEMÁTICO PURO. CONTRIBUYÓ DE MANERA
SIGNIFICATIVA EN EL AVANCE DE LA MATEMÁTICA, LA GEOMETRÍA Y
LA ARITMÉTICA, DERIVADAS PARTICULARMENTE DE LAS RELACIONES
NUMÉRICAS, Y APLICADAS POR EJEMPLO A LA TEORÍA DE PESOS Y MEDIDAS, A
LA TEORÍA DE LA MÚSICA O A LA ASTRONOMÍA
EL INTERÉS DE PITÁGORAS ERA EL DE «LOS PRINCIPIOS» DE LA MATEMÁTICA,
«EL CONCEPTO DE NÚMERO», «EL CONCEPTO DE TRIÁNGULO» (U OTRAS
FIGURAS GEOMÉTRICAS) Y LA IDEA ABSTRACTA DE «PRUEBA».

3. PARA EMPEZAR RECORDEMOS:
• LOS TRIÁNGULOS RECTÁNGULOS SON AQUELLOS QUE TIENE UN ÁNGULO
RECTO, ES DECIR DE 90°
• EN TODO TRIÁNGULO RECTÁNGULO EL LADO OPUESTO EL ÁNGULO RECTO,
QUE ES EL DE MAYO LONGITUD, SE LLAMA HIPOTENUSA Y LOS OTROS SON
LOS CATETOS:
CATETO HIPOTENUSA
CATETO

4. ENUNCIAMOS EL TEOREMA:
EN TODO TRIÁNGULO RECTÁNGULO EL CUADRADO
DE LA HIPOTENUSA ES IGUAL A LA SUMA DE LOS
CUADRADOS DE LOS CATETOS
𝒂 𝟐 = 𝒃 𝟐 + 𝒄 𝟐

5. VEAMOS UN EJEMPLO:
52 = 42 + 32
25 = 16 + 9
25 = 25
𝒂 𝟐 = 𝒃 𝟐 + 𝒄 𝟐

6. DE LA FORMULA ANTERIOR PODEMOS
DEDUCIR LO SIGUIENTE:
𝒂 𝟐
= 𝒃 𝟐
+ 𝒄 𝟐
𝑎 = 𝑏2 + 𝑐2
𝑏 = 𝑎2 − 𝑐2
𝑐 = 𝑎2 − 𝑏2

7. ¿CUAL ES SU UTILIDAD?
SI SABEMOS LA MEDIDA DE DOS LADOS DE UN TRIÁNGULO RECTÁNGULO, PODEMOS
ENCONTRAR LA MEDIDA DEL LADO RESTANTE UTILIZANDO ESTE TEOREMA.
POR EJEMPLO:
𝑎 = 10𝑐𝑚 𝑏 = 102 − 82
𝑏 = ? 𝑏 = 100 − 64
𝑏 = 36
𝑐 = 8𝑐𝑚 𝑏 = 6 𝑐𝑚

8. APLICACIONES
PODEMOS ENCONTRAR DIVERSAS
APLICACIONES TANTO EN EL CAMPO DE
LA MATEMÁTICAS COMO EN
SITUACIONES EXTRA-MATEMÁTICAS

9. APLICACIONES:
RESOLVEMOS:
2,5𝑚 X
9𝑚
𝑥 = 92 + 2,52
𝑥 = 9,34𝑚
PROBLEMA:
UNA PALOMA ESTÁ POSADA EN EL
EXTREMO DE UNA ANTENA DE 2,5M DE
ALTURA; OTRA PALOMA ESTÁ EN UN
BEBEDERO UBICADO A 9M DE LA BASE DE
LA ANTENA.
¿A QUÉ DISTANCIA SE ENCUENTRAN LAS
PALOMAS ENTRE SÍ?
(SUGERENCIA: VUELQUEN LOS DATOS EN
UNA FIGURA DE ANÁLISIS).

10. APLICACIONES:

11. CLASE PENSADA PARA REPASAR TEOREMA DE
PITÁGORAS Y SUS APLICACIONES
DESTINADA A ALUMNOS DE 4TO AÑO
PROFESORA: BELLOMO, FLORENCIA

12. BIBLIOGRAFÍA:
• Ferraris,L y marcha,M.A. “Una puerta abierta a la matemática. Trigonometría”.
2008. Primera edición. Córdoba-Argentina. Ed: Comunicarte.
WEBGRAFÍAS:
• http://www.sectormatematica.cl/basica/santillana/teorema_pitagoras.pdf
• http://www.disfrutalasmatematicas.com/geometria/teorema-pitagoras.html
• http://www.profesorenlinea.cl/geometria/PitagorasTeorema.htm
• https://www.youtube.com/watch?v=GeSiN6vpNS0
• http://es.wikipedia.org/wiki/Pit%C3%A1goras
• http://www.ceibal.edu.uy/UserFiles/P0001/ODEA/ORIGINAL/111107_teorema_
pitagoras.elp/para_qu_sirve.html