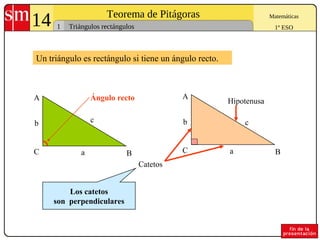
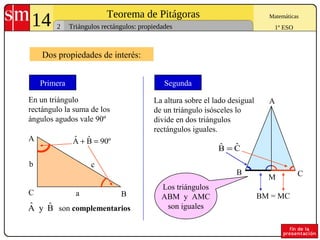
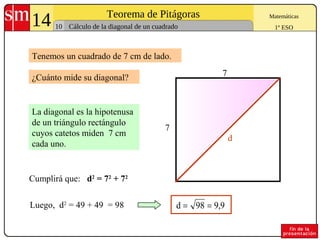
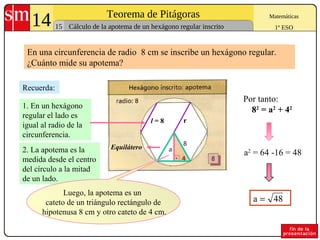
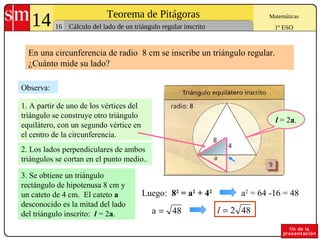
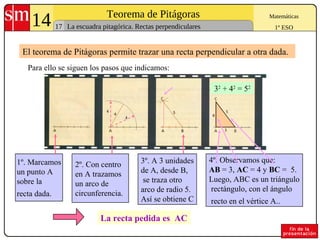
El documento explica el Teorema de Pitágoras, que establece que en cualquier triángulo rectángulo la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa. Se presentan ejemplos para comprobar el teorema y problemas para aplicarlo al cálculo de lados y diagonales de figuras geométricas.

1. 14 Teorema de Pitágoras
1
Matemáticas
1º ESOTriángulos rectángulos
Un triángulo es rectángulo si tiene un ángulo recto.
C B
A
a
cb
Ángulo recto
Los catetos
son perpendiculares
Hipotenusa
C B
A
a
cb
Catetos

2. 14 Teorema de Pitágoras
2
Matemáticas
1º ESOTriángulos rectángulos: propiedades
Dos propiedades de interés:
C B
A
a
cb
Primera
En un triángulo
rectángulo la suma de los
ángulos agudos vale 90º
90ºBˆAˆ =+
Segunda
La altura sobre el lado desigual
de un triángulo isósceles lo
divide en dos triángulos
rectángulos iguales.
A
B CM
BM = MC
CˆBˆ =
Los triángulos
ABM y AMC
son igualesBˆyAˆ son complementarios

3. 14 Teorema de Pitágoras
3
Matemáticas
1º ESOTeorema de Pitágoras: idea intuitiva
En un triángulo rectángulo:
a
c
b
Área = a2
Área = c2
Área = b2
el área del cuadrado construido
sobre la hipotenusa
es igual
a la suma de las áreas de los
cuadrados
construidos sobre los catetos
c2
= a2
+ b2

4. 14 Teorema de Pitágoras
4
Matemáticas
1º ESOTeorema de Pitágoras: comprobación
Por tanto: 32
+ 42
= 52
3
4
Consideramos un triángulo rectángulo de catetos 3 y 4 cm
El área del cuadrado
construido sobre el
primer cateto vale 9
Hay 3·3 = 9
cuadraditos
El área del cuadrado
construido sobre el
segundo cateto vale 16
Hay 4·4 = 16
cuadraditos
Hallemos el área del
cuadrado construido
sobre la hipotenusa.
Observa:
1. El área del triángulo es 6
2. El cuadrado sobre la
hipotenusa contiene 4
triángulos de área 6.
Además contiene un
cuadradito de área 1.
3. Su área total es 6·4 + 1 = 25.
Luego es un cuadrado de lado 5

5. 14 Teorema de Pitágoras
5
Matemáticas
1º ESOTeorema de Pitágoras: segunda comprobación
Consideramos un cuadrado de 7 cm de lado. Su área será 49 cm2
Cuatro triángulos
rectángulos de
catetos 3 y 4 cm.
Cuyas áreas valen
6 cm2
cada uno.
4
3
7
Observa que en ese
cuadrado caben:
Además cabe un
cuadrado de lado c,
cuya superficie es c2
.
Se tiene pues:
49 = 4·6 + c2
c2
= 49 - 24 = 25
c2
= 25 = 52
c2
25 cm2
25 = 9 + 16
Por tanto, 52
= 32
+ 42
6 cm2
c

6. 14 Teorema de Pitágoras
6
Matemáticas
1º ESOTeorema de Pitágoras: ejercicio primero
En un triángulo rectángulo los catetos miden 5 y 12 cm, calcula la
hipotenusa.
5
12
c?
Como c2
= a2
+ b2
se tiene:
c2
= 52
+ 122
= 25 + 144 = 169 c = 13 cm
Haciendo la
raíz cuadrada

7. 14 Teorema de Pitágoras
7
Matemáticas
1º ESOTeorema de Pitágoras: ejercicio segundo
En un triángulo rectángulo un cateto mide 6 cm y la hipotenusa 10 cm.
Calcula el valor del otro cateto.
6
a?
10
Como c2
= a2
+ b2
se tiene:
a2
= 102
- 62
= 100 - 36 = 64
a = 8 cm
a2
= c2
- b2
Luego:
Haciendo la raíz cuadrada:

8. 14 Teorema de Pitágoras
8
Matemáticas
1º ESOLos triángulos “sagrados”
Fueron muy
utilizados por
los arquitectos
y agrimensores
egipcios.
Las medidas de
sus lados son:
3, 4 y 5
o
5, 12 y 13
(También las
proporcionales
a estas)
5 4
3
13
5
12
Todos ellos son
rectángulos,
pues cumplen
la relación:
a2
+ b2
= c2
32
+ 42
= 52
62
+ 82
= 102
92
+ 122
= 152
52
+122
= 132
10
6
8
15
9
12

9. 14 Teorema de Pitágoras
9
Matemáticas
1º ESOReconociendo triángulos rectángulos
Un carpintero ha construido un marco de ventana. Sus dimensiones son
60 cm de ancho y 80 de largo.
Como los lados de la ventana
y la diagonal deben formar
un triángulo rectángulo, tiene
que cumplirse que:
a2
+ b2
= c2
Pero 602
+ 802
= 3600 + 6400 = 10000 La ventana está
mal construida
80 cm
¿Estará bien construido si la
diagonal mide 102 cm?
a
b
c
Mientras que 1022
= 10404
Son distintos
60cm
102 cm

10. 14 Teorema de Pitágoras
10
Matemáticas
1º ESOCálculo de la diagonal de un cuadrado
Tenemos un cuadrado de 7 cm de lado.
La diagonal es la hipotenusa
de un triángulo rectángulo
cuyos catetos miden 7 cm
cada uno.
Luego, d2
= 49 + 49 = 98
¿Cuánto mide su diagonal?
7
7
d
Cumplirá que: d2
= 72
+ 72
9,998d ==

11. 14 Teorema de Pitágoras
11
Matemáticas
1º ESOCálculo de la diagonal de un rectángulo
Tenemos un rectángulo cuyos lados miden 6 y 8 cm.
La diagonal es la hipotenusa
de un triángulo rectángulo
cuyos catetos miden 6 y 8
cm, respectivamente.
Luego, d2
= 36 + 64 = 100
¿Cuánto mide su diagonal?
6
8
d
Cumplirá que: d2
= 62
+ 82
d = 10

12. 14 Teorema de Pitágoras
12
Matemáticas
1º ESOCálculo de la altura de un triángulo isósceles
Tenemos un triángulo isósceles cuyos lados iguales 8 cm, y el otro 6 cm.
La altura es un
cateto de un
triángulo rectángulo
cuyo hipotenusa
miden 8 cm y el otro
cateto 3 cm.
Luego, 64 = 9 + h2
¿Cuánto mide su altura?
6
8 Cumplirá que: 82
= 32
+ h2
Como se sabe, la altura
es perpendicular a la base y
la divide en dos partes
iguales
h
3 3
h2
= 55
4,755h ==
8

13. 14 Teorema de Pitágoras
13
Matemáticas
1º ESOCálculo de la apotema de un hexágono regular
Tenemos un hexágono regular de lado 6 cm. ¿Cuánto mide su apotema?
a2
= 36 - 9 = 27
Luego, la apotema es un cateto
de un triángulo rectángulo de
hipotenusa 6 cm y otro cateto 3.
Recuerda:
Cumplirá que: 62
= a2
+ 32
1. La apotema es la medida
desde el centro del hexágono a
la mitad de un lado.
2. En un hexágono regular la
distancia del centro a cualquiera
de los vértices es igual al lado.
27a =
3 3
6

14. 14 Teorema de Pitágoras
14
Matemáticas
1º ESOCálculo del lado de un cuadrado inscrito en una circunferencia
En una circunferencia de radio 5 cm se inscribe un
cuadrado. ¿Cuánto mide su lado?
Luego, el lado del cuadrado es la
hipotenusa de un triángulo
rectángulo de catetos 5 y 5 cm
Observa:
Entonces: c2
= 52
+ 52
= 50
1. La distancia del centro del
cuadrado a cada uno de sus
vértices es igual al radio: 5 cm.
2. Se forman cuatro ángulos de
90º grados cada uno.
50c =
90º
5
5
c

15. 14 Teorema de Pitágoras
15
Matemáticas
1º ESOCálculo de la apotema de un hexágono regular inscrito
a2
= 64 -16 = 48
Recuerda:
Por tanto:
82
= a2
+ 42
2. La apotema es la
medida desde el centro
del círculo a la mitad
de un lado.
1. En un hexágono
regular el lado es
igual al radio de la
circunferencia.
48a =
En una circunferencia de radio 8 cm se inscribe un hexágono regular.
¿Cuánto mide su apotema?
rl = 8
Equilátero
Luego, la apotema es un
cateto de un triángulo rectángulo de
hipotenusa 8 cm y otro cateto de 4 cm.

16. 14 Teorema de Pitágoras
16
Matemáticas
1º ESOCálculo del lado de un triángulo regular inscrito
a2
= 64 -16 = 48
Observa:
Luego: 82
= a2
+ 42
2. Los lados perpendiculares de ambos
triángulos se cortan en el punto medio..
1. A partir de uno de los vértices del
triángulo se construye otro triángulo
equilátero, con un segundo vértice en
el centro de la circunferencia.
48a =
En una circunferencia de radio 8 cm se inscribe un triángulo regular.
¿Cuánto mide su lado?
3. Se obtiene un triángulo
rectángulo de hipotenusa 8 cm y
un cateto de 4 cm. El cateto a
desconocido es la mitad del lado
del triángulo inscrito: l = 2a.
l = 2a.
482=l

17. 14 Teorema de Pitágoras
17
Matemáticas
1º ESOLa escuadra pitagórica. Rectas perpendiculares
El teorema de Pitágoras permite trazar una recta perpendicular a otra dada.
Para ello se siguen los pasos que indicamos:
1º. Marcamos
un punto A
sobre la
recta dada.
2º. Con centro
en A trazamos
un arco de
circunferencia.
3º. A 3 unidades
de A, desde B,
se traza otro
arco de radio 5.
Así se obtiene C
4º. Observamos que:
AB = 3, AC = 4 y BC = 5.
Luego, ABC es un triángulo
rectángulo, con el ángulo
recto en el vértice A..
4
4
32
+ 42
= 52
La recta pedida es AC