Teoría de conjuntos, Math, matemática aplicada, Matemáticas discretas

1. Prof. Javier Romero

2. Hablemos de Conjuntos

3. ¿Qué es un conjuntos?
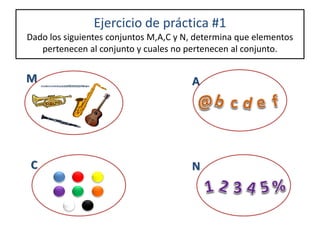
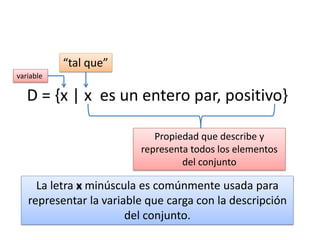
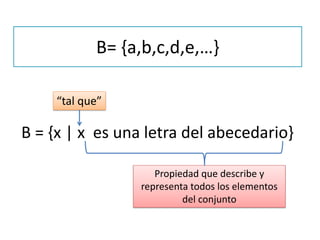
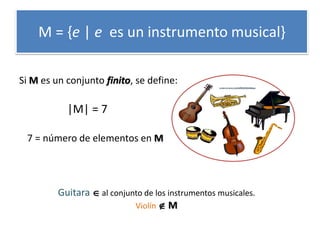
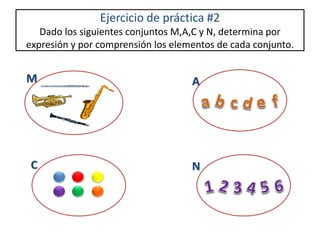
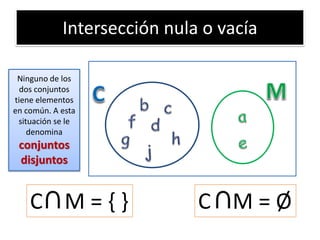
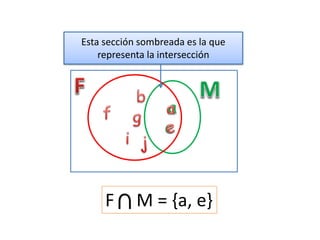
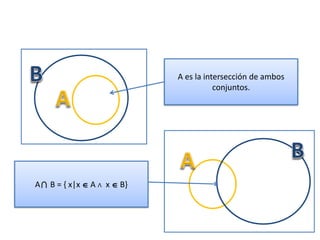
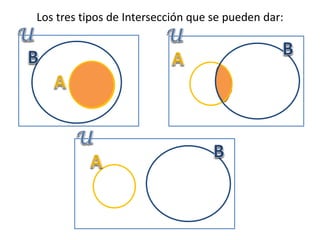
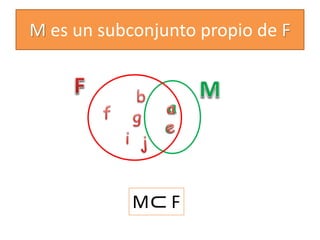
Definimos un conjunto como una colección bien definida de elementos. Se denomina a estos elementos objetos y se dice que son miembros del conjunto.

4. Ejemplos de Conjuntos

5. Conjunto de instrumentos musicales
Una guitara es un elemento del conjunto de los instrumentos musicales.

6. Conjunto figuras geometricas
Cuadrado es elemento del conjunto de figuras geométricas.

7. Conjunto números de 0-9
7 es elemento del conjunto de números

8. El adjetivo “bien definido” implica que cualquiera que sea el objeto considerado, se pueda determinar si está o no en el conjunto que se analiza.

9. Dentro de un conjunto no debe haber elementos repetidos
No cuenta, se elimina del conjunto.

10. Conjuntos letras del abecedario
Para representar conjuntos gráficamente se utilizan los diagramas de Venn-Euler (o diagramas de Venn), los cuales se forman por medio de una línea cerrada, que por lo general tiene forma de círculo o cuadrado.

12. Se utilizan letras mayúsculas, como A, B, C,..., para representar conjuntos, y letras minúsculas o números para representar los elementos.
Conjuntos & Subconjuntos
A = {0,1,2,3,4,5,6,7,8,9}
Ejemplo:

13. Se utilizan llaves { } para organizar los elementos que forman el conjunto.
Conjuntos & Subconjuntos
A = {0,1,2,3,4,5,6,7,8,9}
Ejemplo:

14. Signos de agrupación

15. A = {0,1,2,3,4,5,6,7,8,9}
Por ejemplo: Conjunto A y sus elementos los {números del 0 al 9}
Cada número del 0 al 9, es un elemento del conjunto A.

16. Y= {a,e,i,o,u}
Por ejemplo: El conjunto Y es el conjunto de las {vocales}
Cada vocal es un elemento del conjunto Y.

17. B= {a,b,c,d,e,…}
Por ejemplo: El conjunto B es el conjunto de las {letras del abecedario}
Cada letra es un elemento del conjunto B.

18. Para indicar que un elemento pertenece a un conjunto se usa el símbolo 
a  Y
e  Y
Y= {a,e,i,o,u}
Ejemplos:

19. Para indicar que un elemento NO pertenece a un conjunto se usa el símbolo
p  Y
n  Y
Y= {a,e,i,o,u}
Ejemplos:

20. Si un conjunto es finito y no muy grande, es posible describirlo por la lista de los elementos en el.
A = {0,1,2,3,4,5,6,7,8,9}

21. Un conjunto se determina por sus elementos y no por el orden particular en el que se enumeren.
Así, es lo mismo si el conjunto A se especifica de la siguiente manera:
A = {9,0,6,3,2,1,4,7,5,8}

22. De manera que ni el orden ni la repetición tienen importancia para un conjunto, de modo que A={1, 2, 3}, A={3, 1, 2} A={2, 2, 1, 3}, A={1, 2, 1, 3, 1}.

23. Ejercicio de práctica #1
Dado los siguientes conjuntos M,A,C y N, determina que elementos
pertenecen al conjunto y cuales no pertenecen al conjunto.
M A
C N

24. Por extensión (notación de lista) y por comprensión (notación constructiva)
Un conjunto se puede nombrar o determinar de dos formas:

25. Por extensión
Por extensión o (tabulación) se indica cada uno de los elementos.
A = {0,1,2,3,4,5,6,7,8,9}
Y= {a,e,i,o,u}
Ejemplos:

26. Por comprensión
Por Comprensión se describe la propiedad que caracteriza a todos los elementos del conjunto.
Y= { x | x es una vocal}
A= { z | z es un número del 0 al 9}
Ejemplos:

27. La barra vertical “|” se lee “tal que”.
D = {x | x es un entero par, positivo}
D = {2,4,6,8,10,12…}
La ecuación se leería “D es igual al conjunto de todas las x tales que x es un entero par, positivo”.
Aquí, ser “un entero par, positivo” es la propiedad necesaria para pertenecer al conjunto.
Nota: Observe que la propiedad aparece después de la barra vertical.
variable

28. D = {x | x es un entero par, positivo}
Propiedad que describe y representa todos los elementos del conjunto
“tal que”
La letra x minúscula es comúnmente usada para representar la variable que carga con la descripción del conjunto.
variable

29. B = {x | x es una letra del abecedario}
Propiedad que describe y representa todos los elementos del conjunto
“tal que”
B= {a,b,c,d,e,…}

30. M = {e | e es un instrumento musical}
Guitara  al conjunto de los instrumentos musicales.
Violín  M
Si M es un conjunto finito, se define:
7 = número de elementos en M
|M| = 7

31. Conjunto unitario es aquel conjunto que sólo cuenta con un elemento.
M = {1}
M = {violín}
M = {x|x es un violín}
|M| = 1

32. Ejercicio de práctica #2
Dado los siguientes conjuntos M,A,C y N, determina por
expresión y por comprensión los elementos de cada conjunto.
M A
C N

33. Determina o nombra por expresión y por comprensión
Extensión
Comprensión

35. Operación: UNIÓN DE CONJUNTOS
A ∪ B = A unión B (unión de todos los elementos en A o B)
Se llama unión de dos conjuntos A y B y se escribe A∪B, al conjunto formado por todos los elementos que pertenecen al conjunto A o al conjunto B.
A = {1,2,3,4} + B = {a, b, c}
A ∪ B = {1, 2, 3, a, b, c}
Representa Unión

36. Operación de Unión
A ∪ B = A unión B (unión de todos los elementos en A o B)
A = {9,0,6,3,2,1,4,7,5,8}
B= {a,b,c,d,e,…}
A ∪ B = {9,0,6,3,2,1,4,7,5,8,a,b,c,d,e,…}
Unión = Juntar los elementos de dos o más conjuntos.

37. Operación de Unión
A ∪ B = A unión B (unión de todos los elementos en A o B)
A = {1,2,3,4,5,6,7,8}
B= {2,4,6,8}
A ∪ B = {1,2,3,4,5,6,7,8}
B ⊂ A
A ≠ B
UNIÓN está relacionado al operador

38. El Dr. Pérez observa los record médicos de 10 pacientes y analiza sus síntomas

39. Observemos en un diagrama de conjuntos los pacientes que tienen fiebre y cólicos, fiebre y mareos, cólicos y mareos.

40. Los pacientes que tienen fiebre son:
F = {a, b, e, f, g, i, j}

41. Los pacientes que tienen cólicos son:
C = {b, c, d, f, g, h, j}

42. Los pacientes que tienen mareos son:
M = {a, e}

43. Fiebre y Cólicos
F C = {a,b,e,i,f,j,g,c,d,h}

44. Fiebre y Mareos
F M = {a,b,e,i,f,j,g}

45. Operación: INTERSECCIÓN DE CONJUNTOS
Se llama intersección de dos conjuntos A y B y se escribe A B, al conjunto formado por todos los elementos que pertenecen a la vez al conjunto A y B
∪
INTERSECCIÓN está relacionado al operador

46. Intersección nula o vacía
C M = { }
C M = Ø
Ninguno de los dos conjuntos tiene elementos en común. A esta situación se le denomina conjuntos disjuntos

47. Esta sección sombreada es la que representa la intersección
F M = {a, e}

48. A es la intersección de ambos conjuntos.
A B = { x|x  A ∧ x  B}

49. Los tres tipos de Intersección que se pueden dar:

50. Operación: DIFERENCIA DE CONJUNTOS
La DIFERENCIA entre dos conjuntos A y B la definimos como todos los elementos del primer conjunto que no están incluidos en el segundo conjunto.

51. La diferencia entre A – B La diferencia entre B – A
A - B = {2, 4}
B - A = {5, 8}

52. Sean: A = {3, 4, 5, 6, 7} y B = {4, 6, 7, 8} A - B = {3, 5} B – A = {8}
La diferencia entre A – B La diferencia entre B – A
Recuerda que son todos los elementos del primer conjunto que no están incluidos en el segundo conjunto.

53. Sean: A = {a, b, d, f, g} y B = {a, c, d, e} A - B = {b, f, g} B – A = {c, e}
La diferencia entre A – B La diferencia entre B – A
Recuerda que son todos los elementos del primer conjunto que no están incluidos en el segundo conjunto.

54. Las 4 posibles situaciones de diferencia son:

55. Operación: DIFERENCIA SIMÉTRICA
La diferencia  simétrica, son todos los elementos que pertenecen al conjunto A y al conjunto B pero que no pertenecen a la intersección de AB.

56. A  B = {x|xA  xB  xAB}
A = {2, 4, 6, 8}
B = {1, 2, 3, 4, 5, 6}
AB = {2, 4, 6}
A  B = {1, 3, 5, 8}

57. A  B = {x|xA  xB  xAB}
A = {2, 4, 6, 8}
B = {1, 2, 3, 4, 5, 6}
AB = {2, 4, 6}
A  B = {1, 3, 5, 8}

58. La diferencia simétrica se representa con el símbolo de triangulo
A = {a, b, c, d, f}
B = {a, x, y, z, b}
AB = {a, b}
A  B = {c, d, x, y, f, z}

59. Operación: COMPLEMENTO
Para encontrar el COMPLEMENTO de un conjunto cualquiera, hay que buscar la diferencia entre el U (universo) y el conjunto.
Ā = (U – A)
Todos los elementos del universo que no pertenecen al conjunto A
El símbolo para complemento son:  ó Ā ó A'

60. Operación: COMPLEMENTO
COMPLEMENTO
está relacionado al operador
El símbolo para complemento es
 ó Ā ó A.
A = {x|x UxA}
A = {x|xA}
En otras palabras el complemento de A es igual al Universo menos A.
U = {a, b, c, d, e}
A = {a, b, c}
A = {d, e}

61. Operación: COMPLEMENTO
El complemento de A = {d, e}.
Significa que le falta al conjunto A para ser igual al universo

62. Cuando se trata un problema particular, hay un universo o conjunto universal, formulado o implicado. El universo se denota por U del cual se seleccionan los elementos para formar los conjuntos.

63. Para un universo U se dice que los conjuntos C y D (tomados de U) son iguales y se escribe C = D, si C y D contienen los mismos elementos.

64. Sean A, B, C ⊆ U.
Si A ⊆ B y B ⊆ C, entonces A ⊆ C
Si A ⊂ B y B ⊆ C, entonces A ⊂ C
Si A ⊆ B y B ⊂ C, entonces A ⊂ C
Si A ⊂ B y B ⊂ C, entonces A ⊂ C

65. Sea U = {1, 2, 3, 4, 5} con A = {1, 2, 3}, B = {3,4}, C = {1, 2, 3, 4}. Entonces se cumplen las siguientes relaciones de subconjuntos:
a) A ⊆ C
b) A ⊂ C
c) B ⊂ C
d) A ⊆ A
e) B ⊊ A (es decir, B no es un subconjunto de A)
f) A ⊄ A

66. Operación: COMPLEMENTO
U = {a, b, c, d, e, f, g, … z}
T = {a, b, c}
T = {d, e, f, g, … z}

67. Operación: COMPLEMENTO
U = {1, 2, 3, 4, 5, 6, 7, 8, …}
E = {1, 3, 5, 7, 9, …}
E = {2, 4, 6, 8,… }
U = {x|x números naturales}
E = {x|x números impares}
E = {x|x números pares}

69. Decimos que A es un subconjunto de B, si todo elemento de A esta incluido en B.
A B
⊂
A es un subconjunto propio de B

70. Símbolos de subconjuntos
Recuerda que este símbolo ⊆ representa subconjunto
Recuerda que este símbolo ⊂ representa subconjunto propio
Los elementos pueden estar incluidos.
Los elementos están estrictamente incluidos.

71. Propiedades de los subconjuntos
Reflexiva =
A ⊆ A ¡es obvia!
Antisimétrica =
A ⊆ B ∧ B ⊆ A por  ende A ⊆ B
Transitiva =
A ⊆ B ∧ B ⊆ C por  ende A ⊆ C

72. M es un subconjunto propio de F
M F

73. Lista de símbolos para conjuntos
•p ∨ q <---> p o q
•p ∧ q <---> p y q
•x  X <---> x es un elemento de X
•x  X <---> x no es un elemento de X
•X = Y <---> igualdad de conjuntos (X y Y tienen los mismos elementos)
•X ≠ Y <---> No son conjuntos iguales
•|X| <---> número de elementos en X
•∅ <---> conjunto vacío
•X ⊆ Y <---> X es un subconjunto de Y
•X ⊂ Y <---> X es un subconjunto propio de Y

74. Algunos ejemplos fueron tomados de: http://mategradosexto.blogspot.com/2013/04/ operaciones-entre-conjuntos.html http://www.unlu.edu.ar/~dcb/matemat/diagvenna1.htm