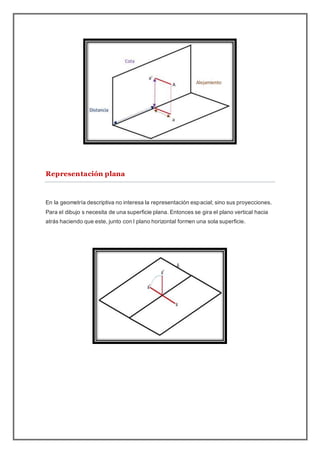
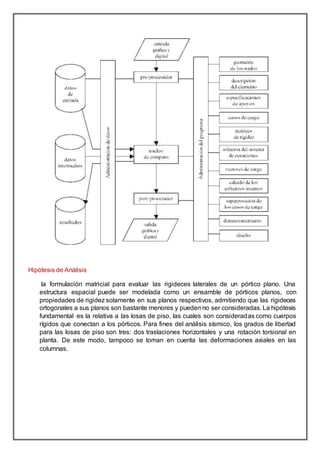
El documento trata sobre el análisis tridimensional de estructuras. Explica conceptos clave como la proyección cilíndrica ortogonal y diferentes tipos de rectas en el espacio tridimensional. También describe hipótesis comunes de análisis estructural y características de programas de análisis, así como armaduras tridimensionales. El objetivo general es estudiar el análisis tridimensional y su importancia para visualizar problemas en el espacio de tres dimensiones.

1. FACULTAD DE INGENIERIA
ESCUELA ACADEMICO PROFESIONAL DE INGENIERIA CIVIL
INFORME ACADEMICO
“ANALISIS TRIDIMENSIONAL DE ESTRUCTURAS”
Autores:
1. .
2. .
3. .
4. .
5. .
Asesor:
Ing. Daniel Albert Diaz Beteta
Huaraz - Perú
2019

2. INTRODUCCIÓN
El análisis tridimensional, se basa en el estudio de la. geometría? descriptiva,
disciplina de carácter formativo que permite visualizar en el plano, problemas en
el espacio de tres dimensiones. Su concepción es fundamental para entender
cabalmente el tema siguiente que es la teoría de las proyecciones. Los
conceptos
Los análisis pueden realizarse considerando un comportamiento lineal fuerza-
desplazamiento del material; eventualmente pueden considerarsecomportamientos
no lineales para los análisis tiempo-historia.Los programasde análisis estructurales
más comunes no realizan análisis incluyendo efectos de segundo orden
(denominado también no linealidad geométrica), es decir, la consideración de
esfuerzos adicionales debidos a la modificación de los ejes causada por las
deformaciones.
Las oscilaciones se producen en los elementos o sistemas estructurales debido a
que tienen masas, elasticidad y una capacidad de amortiguamiento manifestado en
diversas formas. Pararealizar un análisisde la respuesta de estos sistemasse parte
de algunas simplificaciones, con las que se aborda el problema de manera más
sencilla y a menudo suficiente para fines prácticos de ingeniería. Sin embargo,
deben comprenderse las hipótesis iniciales de cada tipo de análisis, pues en ellas
están contenidas sus limitaciones y contribuyen a establecer sus campos de
aplicación.

3. OBJETIVOS
OBJETIVO GENERAL
 El objetivo es el estudio de la tridimensional, permite visualizar en el plano,
problemas en el espacio de tres dimensiones.
 Dar a conocer la importancia del análisis tridimensional, su proyección y su
geometría.
 Dise˜narydesarrollarunservicioWEB,basadoenel modelocliente servidor,
accedible enInternetdesde computadorespersonales(PC),parael an´alisis,dise˜noy
evaluaci´onde estructurasaporticadastridimensionalesde concretoarmado.
OBJETIVO ESPECÍFICO
 Dar a conocer las intersecciones de una recta proyectante que contiene a un
elemento geométrico del espacio con un plano de proyección. Suponiendo que la
recta proyectante y el plano de proyección forman un ángulo recto, de donde las
proyecciones reciben el nombre de proyecciones ortogonales, es decir la
proyección cilíndrica ortogonal.
 Dar a conocer todo lo referente a la idea de dimensión que alude a la cantidad
más pequeña de coordenadas tridimensionales que se necesitan para ubicar un
punto en el plano.
 Realizar el análisis y diseño de la estructura de concreto, tomando en
cuenta condiciones del subsuelo y los requisitos de reglamento para
concreto estructural (ACI 318-05).

4. Proyección cilíndrica ortogonal
El análisis tridimensional, se basa en el estudio de la. geometría? descriptiva,
disciplina de carácter formativo que permite visualizar en el plano, problemas
en el espacio de tres dimensiones.
un comportamiento lineal fuerza-desplazamiento del material; eventualmente
pueden considerarse comportamientos no lineales para los análisis tiempo-
historia. Los programas de análisis estructurales más comunes no realizan
análisis incluyendo efectos de segundo orden (denominado también no
linealidad geométrica), es decir, la consideración de esfuerzos adicionales
debidos a la modificación de los ejes causada por las deformaciones.
Las oscilaciones se producen en los elementos o sistemas estructurales debido
a que tienen masas, elasticidad y una capacidad de amortiguamiento
manifestado en diversas formas. Para realizar un análisis de la respuesta de
estos sistemas se parte de algunas simplificaciones, con las que se aborda el
problema de manera más sencilla y a menudo suficiente para fines prácticos de
ingeniería. Sin embargo, deben comprenderse las hipótesis iniciales de cada
tipo de análisis, pues en ellas están contenidas sus limitaciones y contribuyen a
establecer sus campos de aplicación.
Es la intersección de una recta proyectante que contiene a un elemento
geométrico del espacio con un plano de proyección. Suponiendo que la recta
proyectante y el plano de proyección forman un ángulo recto, de donde las
proyecciones reciben el nombre de proyecciones ortogonales, es decir la
proyección cilíndrica ortogonal.
Los planos de proyección se identifican como plano horizontal y plano frontal.
La región del plano frontal comprende el I y II cuadrante, esta región se
denomina como plano frontal superior (PFS) y la región comprendida en entre
los cuadrantes III y IV, se denomina plano horizontal anterior (PHA). De la
misma forma, para el plano horizontal comprendido entre los cuadrantes I y IV
lo identificaremos como plano horizontal anterior (PHA), mientras que la región
correspondiente a los cuadrantes II y III, se identifica como plano horizontal
posterior (PHP).

5. las proyecciones del punto A, la proyección presente en el plano horizontal
anterior se designó con la letra minúscula correspondiente a la que identifica el
elemento geométrico en el espacio, y la proyección frontal con la misma letra
minúscula pero acompañada de un apóstrofo “ ’ ”, la recta de intersección de
los planos de proyección se conoce como línea de tierra y se identifica por dos
segmentos de recta contenidos en la proyección horizontal.
Planos de proyección
Se usan dos planos de proyección, uno horizontal y otro perpendicular a este, vertical. Por
lo que cualquier punto A en el espacio (Fig. No. 2) tendrá dos proyecciones en el plano
horizontal y A’ en el plano vertical. La intersección de los planos, la recta IT, se denomina
línea de tierra.
Las líneas de proyección horizontal A a Y vertical A a son perpendiculares entre sí y
perpendiculares a sus respectivos planos de proyección.

6. Representación plana
En la geometría descriptiva no interesa la representación espacial; sino sus proyecciones.
Para el dibujo s necesita de una superficie plana. Entonces se gira el plano vertical hacia
atrás haciendo que este, junto con l plano horizontal formen una sola superficie.

7. Recta fronto-horizontal
Es una recta paralela tanto al plano horizontal, como al plano frontal de
proyección (vertical) y debido a que estamos en la proyección cilíndrica ortogonal
sus proyecciones diédricas resultan paralelas a la línea de tierra, por lo que en
ambas proyecciones aparece la magnitud real de la recta (MR). Por ser paralela
a ambos planos, el ángulo que existe entre ellos resulta nulo.

8. Recta frontal
Este tipo de recta es paralela al plano frontal de proyección, (por lo que sus
alejamientos son constantes) pero oblicua con respecto al plano horizontal de
proyección, su magnitud real aparece en la proyección frontal, este tipo de recta
forma un Angulo en el plano horizontal que suele denominarse α (aunque se
puede asignar cualquier otra sigla) y tal ángulo aparece también en las
proyecciones diédricas en magnitud real.
CARACTERISTICAS DE LOS PROGRAMAS DE ANALISIS
Los programas de análisis estructural son desarrollados principalmente para
estructuras de concreto armado, sean aporticadas, con muros o mixtos; también
es posible analizar estructuras de acero o una mixtura de ambos materiales. Para
los análisis no lineales, existen programas que consideran la no linealidad del
material y otros que incluyen también la no linealidad geométrica (para
considerar el efecto de segundo orden de las cargas); se tienen diferentes
opciones de modelos histeréticos, de acuerdo a los distintos materiales y las
distintas teorías de comportamiento no lineal. En la Figura 9 se presenta un
esquema del desarrollo de las operaciones de un programa de análisis
estructural.

9. Hipótesis de Análisis
la formulación matricial para evaluar las rigideces laterales de un pórtico plano. Una
estructura espacial puede ser modelada como un ensamble de pórticos planos, con
propiedades de rigidez solamente en sus planos respectivos, admitiendo que las rigideces
ortogonales a sus planos son bastante menores y pueden no ser consideradas. La hipótesis
fundamental es la relativa a las losas de piso, las cuales son consideradas como cuerpos
rígidos que conectan a los pórticos. Para fines del análisis sísmico, los grados de libertad
para las losas de piso son tres: dos traslaciones horizontales y una rotación torsional en
planta. De este modo, tampoco se toman en cuenta las deformaciones axiales en las
columnas.

10. ARMADURA TRIDIMENSIONAL
Son ensambles triangulares que distribuyen cargas a los soportes a través de
una combinación de miembros conectados por juntas articuladas
configuradas en triángulos de manera que todos estén en compresión o
tensión pura (sin flexión o cortante) y todas las fuerzas de empuje se
descomponen internamente.
La estructura tridimensional comogeneradorade espaciossingulares destaca
por su ligereza y grandes luces conseguidas a raíz de una versión
tridimensional de las armaduras planas.
Las estructuras tridimensionales dotan de una enorme flexibilidad a los
edificios.
Sus componentes son elementos rígidos y finos, unidos rígidamente y basados
en formas geométricas como triángulos, hexágonos, octógonos…siempre
buscando el diseño, la estética y la funcionalidad.
Los materiales empleados son el acero y el aluminio, utilizados en menor
cantidad que las estructuras bidimensionales. Las cubiertas que sujetan
habrán de ser ligerascomo condicionante fundamental, pudiendoser de vidrio,
acrílico, policarbonato, láminas metálicas e incluso membranas.
Las posiblesluces que se obtienende esta forma de cubrir sondesde 20 a 200
metros libres sin apoyos intermedios, lo que aporta al espacio una flexibilidad
bastante importante. Por ello, destacan soluciones versátiles con un
importante ahorro de dinero y tiempo, que como ya sabemos van íntimamente
relacionados, aparte del material consumido.
Las barras que conforman el entramado de la estructura de la cubierta
transfieren las cargas solicitadas a las barras que conforman la estructura, con
lo que la optimización en su cálculo se hace de forma necesaria, pudiendo
soportar altas tensiones repartidas d forma uniforme.
Dimensiones
Las posiblesluces que se obtienen de esta forma de cubrir sondesde20 a 200
metros libres sin apoyos intermedios, lo que aporta al espacio una flexibilidad

11. bastante importante. Por ello, destacan soluciones.
Estructura tridimensional ensamblable o fija, sin elementos de unión.
La presente invención se refiere a una estructura tridimensional ensamblable
o fija sinelementos de unión que permiteel enlace o unión entre los elementos
que la integran gracias a que en sus extremos estos cuentan con los medios
de sujeción necesarios para llevarla a cabo directamente entre ellos, para tal
fin la sección transversal de los elementos presenta a todo lo largo o por lo
menos en sus extremos ángulos que permiten que al converger éstos en el
punto de interseccióndos de los lados contiguos de la sección de un elemento
comparta cadauno de ellos, el mismoplano con uno de los lados de la sección
de cada uno de los elementos que quedan a ambos lados de este, lo que
posibilita su unión fija, por medio de soldadura por resistencia eléctrica
(soldadura por puntos) u otros medios
RESOLUCIÓN DE UNA ARMADURA TRIDIMENSIONAL
 Es primordial conocer la altura para resolverlo. De acuerdo a la figura
tomamos el triángulo ABC debido a que las barras miden lo mismo 1.5
metros, podemos conocer la dimensiónde AC, mediante el teorema de
Pitágoras.
 Ahora con el nuevo dato obtenido y el triángulo ABC, construimos otro
triángulo que nos dará la altura de la armadura y nuevamente se utiliza
el teorema de Pitágoras. Utilizando triángulos proporcionales se
conocerá los componentes de los vectores de las fuerzas, la proporción
esta dada en dos triángulos uno expresado en distancia y otro en
fuerza, de esa manera la dimensión de la fuerza expresada en “X”. Se
saca la dimensión de la componente en “X”.
 Se realiza una tabla en donde se muestran las componentes de X, Y y
Z y se muestran de un lado las fuerzas y de otro las distancias, en la
distancia de Z se toma la mitad, en la distancia de x es una distancia de
1.5 y la mitad sería 0.75 al igual que en el eje de las Y en X y Y se toma
la misma fórmula, pero en Z se sustituye
El caso general de estructuras es el de pórticos en el espacio cuyos nudos tienen
seis grados de libertad, correspondientes a tres desplazamientos y tres rotaciones
.

13. Ejemplo de Aplicación
Se desarrollará el análisis de una estructura a porticada de concreto armado
(E=2x106 t/m2) de un piso, considerando que el diafragma de piso es
suficientemente rígido para realizar el análisis con un modelo tridimensional. La
fuerza aplicada F es de 10 toneladas, como se indica en la figura.
Tipo I
Matriz de Rigidez

14. Matriz de Rigidez:
Pórtico Tipo II

15. Definición de la Matriz de Rigidez de la Estructura
Considerando:
~ x = 450 cm, yo = 450 cm
Además, para cada pórtico:
Matriz de Rigidez Total

16. Donde
Al realizar las operaciones, se obtiene
Determinación de los desplazamientos de piso:
Desplazamientos de los Pórticos. Ejemplos:pórticos 3 y 1. d.1) Pórtico 3
Reemplazando

17. Pórtico 1
Momentos Flectores
Columna Interior:
Viga Izquierda:
D.M.F.

19. CONCLUSIÓN
 Del presente informe, podemos concluir que para poder realizar una vista
en tres dimensiones (3D) a parte de reconocer las partes de la fotografía,
también debemos tener en cuenta la distancia instrumental del
estereoscopio, para poder ubicar las fotografías, logrando así una buena
visión de las imágenes y reconocimiento del medio, de esta manera al
momento de tomar medidas en la fotografía y reemplazarlas en las
formulas necesarias el error será mínimo

20. REFERENCIAS BIBLIOGRAFICAS
 Arenas González, Alfredo (1999). «Tema 2». Universidad Nacional
Autónoma de México, ed. Cuaderno de Apuntes de "Análisis
Tridimensional". Ciudad Universitaria, México, D.F. C.P. 04510: Facultad
de Ingeniería. p. 87.
 ↑ Campos Newman, Luis E. Epítome de Geometría Descriptiva.
 Celig¨ueta Lizarza, J. T. (2008). M´etodo de los Elementos Finitos para An´alisis
Estructural. Navarra, Espa˜na.
 Chaves Eduardo, M. R. (2010). Mec´anica computacional en la ingenier´ıa con
aplicaciones en MATLAB. Ciudad Real, Espa˜na. Comer, D. E. (1995). Redes
globales de informaci´on con internet y TCP/IP.
 Pearson Education, M´exico. Computers and Structures, INC. (2012a). ETABS
Overview.
 http://www.csiberkeley.com/etabs. Computers and Structures, INC. (2012b).
SAP2000 Overview. http://www.csiberkeley.com/sap2000/. Fl´orez L´opez, J.
(1999).

21. ANEXOS
Vista en planta
Análisis de edificaciones
Armaduras tridimensionales