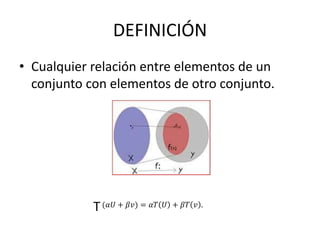
Una transformación lineal es cualquier relación entre elementos de un conjunto y elementos de otro conjunto que cumple ciertas propiedades. Las propiedades incluyen que la transformación de cero es cero, que la transformación de una combinación lineal de vectores es igual a la combinación lineal de las transformaciones de los vectores individuales, y que la transformación de un escalar por un vector es igual al escalar por la transformación del vector. Las transformaciones lineales se utilizan en álgebra lineal y tienen aplicaciones en diversas áreas.

1. TRANSFORMACIÓN LINEAL

2. DEFINICIÓN
• Cualquier relación entre elementos de un
conjunto con elementos de otro conjunto.
T(𝛼𝑈 + 𝛽𝑣) = 𝛼𝑇 𝑈 + 𝛽𝑇 𝑣 .

3. Propiedades
• Propiedad 1:
i) T(0) = 0
i) T(0) = T(0+0) = T(0) + T(0)
0=T(0)-T(0)= T(0) + T(0)- T(0) = T(0)
El cero de la izquierda es el del vector cero en V, mientras que el 0 de la derecha es el
vector cero en W
• Propiedad 2:
Sea V un espacio vectorial de dimensión finita con base B={v1, v2, ..., vn}.
Sean w1, w2, ..., wn n vectores en W.
Suponga que T1 y T2 son dos transformaciones lineales de V en W tales que
T1vi= T2vi = wi para i = 1, 2, ..., n.
Entonces para cualquier vector v ∈ V, T1v = T2v. Es decir T1 = T2.
• Propiedad 3:
T(a1v1+a2v2+…+anvn) = a1T(v1 ) +a2T(v2 ) +…+anT(vn )
La transformación de un escalar por un vector debe ser igual al escalar por la
transformada de un vector.

4. Ejemplos de las propiedades
• T(0) = 0
• T(0) = T(0+0) = T(0) + T(0).
• 0 = T(0) – T(0) = T(0) + T(0) – T(0) = T(0).
• T (u+v) = T (u) + T (v)
• u= (a,b) T (u)= (3a, a-b)
• v= (c,d) T (v)= (3c,c-d)
• u+v= (a+c,b+d)
• T (u+v)= (3a+3c, (a-b)+(c-d) )
• T (u+v)= (3a,a-b)+ (3c,c-d)
• T(cu)= cT(u)
• cu= (ca,cb) T (cu)= (3ca,ca-cb)
• T (cu)= c (3a,a-b)

5. Bibliografía
Stanley I. Grossman: "Algebra Lineal", Segunda Edición;
Grupo Editorial Iberoamérica
https://www.youtube.com/watch?v=akvDOCPSoIw