Este documento describe la transformada Z, la cual convierte una señal de tiempo discreto a una representación en el dominio de la frecuencia. La transformada Z es análoga a la transformada de Laplace para señales de tiempo continuo. Se define la transformada Z bilateral y unilateral, y se explican conceptos como polos, ceros y región de convergencia. Finalmente, se presentan ejemplos para calcular la transformada Z inversa.

1. REPÚBLICA BOLIVARIANA DE VENEZUELA
INSTITUTO UNIVERSITARIO POLITÉCNICO
“SANTIAGO MARIÑO”
ESCUELA DE INGENIERÍA ELECTRÓNICA
EXTENSIÓN MATURÍN
TRANSFORMADA Z
Materia: Realizado por:
Teoría Moderna de Control Luis Requena
C.I 25.274.444
Maturín, Febrero de 2017.

2. Mapa conceptual

3. La Transformada Z convierte una señal real o compleja definida en el
dominio del tiempo discreto en una representación en el dominio de la
frecuencia compleja.
El nombre de Transformada Z procede de la variable del dominio. Un
nombre más adecuado para la TZ podría haber sido Transformada de Laurent, ya
que está basada en la serie de Laurent. La TZ es a las señales de tiempo discreto
lo mismo que Laplace a las señales de tiempo continuo.
Es un modelo matemático que se emplea entre otras aplicaciones en el
estudio del Procesamiento de Señales Digitales, como son el análisis de Circuitos
Digitales, los Sistemas de Radar o Telecomunicaciones y especialmente los
Sistemas de Control de Procesos por computadoras.
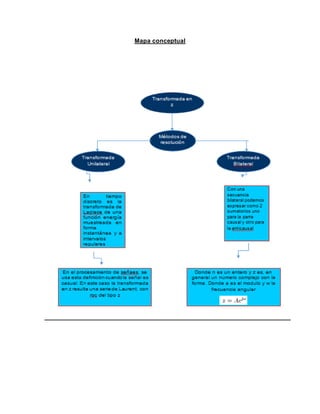
La transformada Z, al igual que otras transformaciones integrales, puede ser
definida como una transformada unilateral o bilateral.
 Transformada Z bilateral
La TZ bilateral de una señal definida en el dominio del tiempo discreto x[n] es
una función 𝑋(𝑧) que se define
Donde n es un entero y z es, en general, un número complejo de la forma
Donde A es el módulo de z, y ω es el argumento de ese complejo que bien
podría representar la frecuencia angular (pulsación) en radianes por segundo
(rad/s).

4.  Transformada Z unilateral
De forma alternativa, en los casos en que x[n] está definida únicamente
para n ≥ 0, la transformada Z unilateral se define como
En el procesamiento de señales, se usa esta definición cuando la señal
es causal. En este caso, la Transformada Z resulta una serie de Laurent, con RDC
del tipo ; es decir que converge hacia afuera.
Un ejemplo interesante de la TZ unilateral es la función de generación de
probabilidades, donde x[n] es la probabilidad que toma una variable
discreta aleatoria en el instante n, y la función X(z) suele escribirse como X(s), ya
que s = z−1
. Las propiedades de las transformadas Z son útiles en la teoría de la
probabilidad
La transformada Z puede mostrarse gráficamente mediante su diagrama
de polos y ceros. Los polos se representan mediante aspas y los ceros
mediante círculos.
Si se dispone de una expresión de la transformada Z que utilice polos y
ceros:
Las posiciones de los polos determinan la frontera de la RDC, ya que la
RDC no puede contenerlos.
Si x(n) es causal, la RDC se extiende del polo más externo al infinito

5. Ej: x(n) causal
𝑋(𝑧) = 2
1 − 0.5𝑧−1
1 + 2𝑧−2
Transformada z inversa
Formalmente la transformada z inversa de define como:
Donde el contorno cerrado de integración es en el plano complejo. La
definición de tal contorno implica unos requerimientos matemáticos fuera del
alcance de este trabajo. Para fines prácticos es suficiente encontrar x[n]
mediante el método de las fracciones simples tal y como se indica en el ejemplo
siguiente:
Ejemplo: Una señal x[n] tiene la transformada z definida por la
ecuación:
Calcular x[n] . Solución
EJERCICIOS
Ejemplo 1
Usando el método por la transformada en z inversa
Método de expansión en fracciones parciales.
Halle X[n] para n = 0, 1, 2, 3, 4, cuando

6. Solución
Dividiendo el numerador por el denominador se obtiene:
X[Z]=10Z-1
+17Z-2
+18.4Z-3
+18.68Z-4
+ ...
Al comparar esta expansión X[Z] en una serie infinita
Se obtiene: X[0]=0, X[1]=10, X[2]=17, X[3]=18.4, x[4]=18.68
En la mayoría de los casos no resulta tan sencillo identificar el término general
mediante la observación de algunos valores de la secuencia.
El método más utilizado es la descomposición en fracciones parciales de
X[Z]. En vista de la unicidad de la transformada Z, se puede utilizar la tabla de
parejas de transformadas para identificar las secuencias correspondientes
Ejemplo 2
Usando el método por la transformada en z inversa
Método de la integral de inversión
Para hacer más didáctico el proceso de conceptualización de la Transformada
Inversa, se cumplimentarán los siguientes pasos:

7.  Se considerará un pulso de ancho 2.a y altura 1.
 A este pulso se le hallará la Transformada de Fourier [F(w)]. De modo que,
en el proceso de inversión, se conozca el resultado exacto con el objeto de
realizar comparaciones.
 Finalmente se aplicará la Fórmula de Inversión (7-2) para hallar fs(t).
Para hallar la Transformada de Fourier, se hace uso de (6-1):
Se requiere hacer el proceso inverso (Antitransformada)

8. Donde:
Es la llamada función Seno Integral. Existen tablas para calcular sus
valores, pero resultará más práctico resolver el problema a través de Mathcad.
Si ahora se
observa el gráfico resultante: