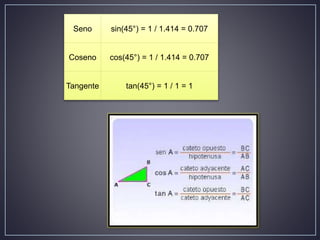
La trigonometría estudia las relaciones entre los lados y ángulos de los triángulos. Se define el seno, coseno y tangente de un ángulo como las razones entre los lados opuestos, adyacentes e hipotenusa de un triángulo rectángulo. Estas funciones trigonométricas junto con la cosecante, secante y cotangente se aplican en campos como la geometría, medición y otras áreas donde se requiere precisión.

2. La trigonometría es una rama de la matemática, cuyo significado
etimológico es 'la medición de los triángulos'. Deriva de los
términos griegos τριγωνο trígono 'triángulo' y μετρον metron 'medida'.
En términos generales, la trigonometría es el estudio de las razones
trigonométricas: seno, coseno; tangente,
cotangente; secante y cosecante. Interviene directa o indirectamente en
las demás ramas de la matemática y se aplica en todos aquellos ámbitos
donde se requieren medidas de precisión. La trigonometría se aplica a
otras ramas de la geometría, como es el caso del estudio de las esferas
en la geometría del espacio.

3. Un ángulo es la región del plano comprendida entre dos semirrectas
con origen común.
A las semirrectas se las llama lados del ángulo. El origen común es
el vértice.
El ángulo es positivo si se desplaza en sentido contrario al movimiento
de las agujas del reloj y negativo en caso contrario

4. Antes de concentrarnos en las funciones, nos ayudará dar
nombres a los lados de un triángulo rectángulo, de esta manera:

5. Las tres funciones más importantes en trigonometría son el seno,
el coseno y la tangente. Cada una es la longitud de un lado
dividida entre la longitud de otro
Para el ángulo θ:
Función seno: sin(θ) = Opuesto / Hipotenusa
Función
coseno:
cos(θ) = Adyacente / Hipotenusa
Función
tangente:
tan(θ) = Opuesto / Adyacente

6. o El seno (abreviado como sen, o sin por llamarse "sĭnus" en
latín) es la razón entre el cateto opuesto sobre la hipotenusa.
o El coseno (abreviado como cos) es la razón entre el cateto
adyacente sobre la hipotenusa.

7. o La tangente (abreviado como tan o tg) es la razón entre el
cateto opuesto sobre el cateto adyacente.
Ejemplo 1: ¿cuáles son el seno, coseno y tangente de 30° ?
El triángulo clásico de 30° tiene hipotenusa de longitud 2, lado
opuesto de longitud 1 y lado adyacente de longitud √3:

8. Seno sin(30°) = 1 / 2 = 0.5
Coseno cos(30°) = 1.732 / 2 = 0.866
Tangente tan(30°) = 1 / 1.732 = 0.577
Ejemplo 2: ¿cuáles son el seno, coseno y tangente de 45°?
El triángulo clásico de 45° tiene dos lados de 1 e hipotenusa
√2:

9. Seno sin(45°) = 1 / 1.414 = 0.707
Coseno cos(45°) = 1 / 1.414 = 0.707
Tangente tan(45°) = 1 / 1 = 1

10. • La Cosecante: (abreviado como csc o cosec) es la razón inversa
de seno, o también su inverso multiplicativo:

11. • La Secante: (abreviado como sec) es la razón inversa de
coseno, o también su inverso multiplicativo:
• La Cotangente: (abreviado como cot o cta) es la razón inversa
de la tangente, o también su inverso multiplicativo:

12. Ejemplo:
Dado el triángulo de lados a= b=2 y c=3, vamos a calcular las
razones trigonométricas asociadas al dicho triángulo.
Entonces:
sin(x)= 2/3 cos(x)= 2/3 tan(x)= 2/2 = 1
Las razones trigonométricas inversas asociadas son:
csc(x)= 3/2 sec(x)= 3/2 cot(x)= 1

13. Normalmente se emplean las relaciones trigonométricas seno,
coseno y tangente, y salvo que haya un interés específico en
hablar de ellos o las expresiones matemáticas se simplifiquen
mucho, los términos cosecante, secante y cotangente no suelen
utilizarse.