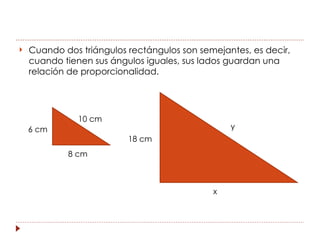
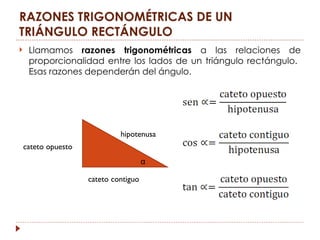
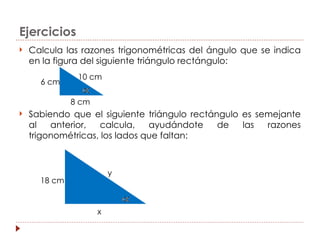
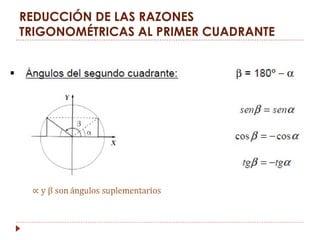
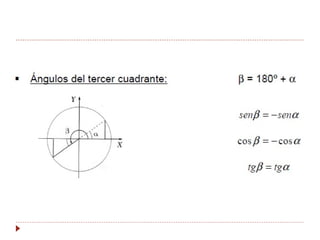
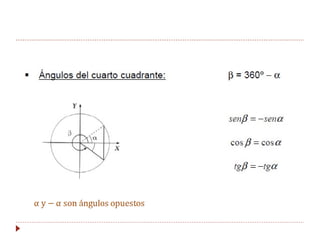
La trigonometría estudia las relaciones entre los lados y ángulos de los triángulos rectángulos. Esto permite calcular alturas y distancias inaccesibles. Las razones trigonométricas (seno, coseno y tangente) relacionan los catetos y la hipotenusa de un triángulo rectángulo con un ángulo dado. La circunferencia goniométrica muestra las razones trigonométricas para cualquier ángulo.

1. TRIGONOMETRÍA
MATEMÁTICAS 4º ESO

2. LA IMPORTANCIA DE LA TRIGONOMETRÍA
 Trigonometría, etimológicamente, significa medida de
triángulos.
 Conocidos dos lados de un triángulo rectángulo, aplicamos
habitualmente el Teorema de Pitágoras para conocer el
tercer lado.
h2 = c12+c22
c1 = 3 cm ¿h?
h = 5 cm
c2 = 4 cm
 Pero, ¿y si lo que conocemos es un lado y un ángulo?
Por ejemplo, podemos medir el ángulo con el que
avistamos una montaña. Luego medimos la distancia desde la
que medimos ese ángulo y la base de la montaña. Con estos
datos deseamos conocer la altura de la montaña. Aquí entra
en juego la trigonometría.

3. APLICACIONES DE LA TRIGONOMETRÍA
 Altura de un edificio  Distancia a un punto
inaccesible
 … entre otras

4.  Cuando dos triángulos rectángulos son semejantes, es decir,
cuando tienen sus ángulos iguales, sus lados guardan una
relación de proporcionalidad.
10 cm
6 cm y
18 cm
8 cm
x

5. RAZONES TRIGONOMÉTRICAS DE UN
TRIÁNGULO RECTÁNGULO
 Llamamos razones trigonométricas a las relaciones de
proporcionalidad entre los lados de un triángulo rectángulo.
Esas razones dependerán del ángulo.
hipotenusa
cateto opuesto
α
cateto contiguo

6. Ejercicios
 Calcula las razones trigonométricas del ángulo que se indica
en la figura del siguiente triángulo rectángulo:
10 cm
6 cm
8 cm
 Sabiendo que el siguiente triángulo rectángulo es semejante
al anterior, calcula, ayudándote de las razones
trigonométricas, los lados que faltan:
y
18 cm
x

7. RAZONES TRIGONOMÉTRICAS DE
ÁNGULOS IMPORTANTES
sen cos tan
45º
30º
60º

8. RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO
CUALQUIERA:
LA CIRCUNFERENCIA GONIOMÉTRICA

9. Ejercicios
 Indica en qué cuadrante se encuentran los siguientes ángulos
y el signo de sus razones trigonométricas:
IMPORTANTE: El radián es una unidad de medida de ángulos que se define
como el ángulo determinado por un arco de circunferencia cuya longitud
coincide con el radio de dicha circunferencia.
El factor de conversión de radianes a grados es:

10. RELACIONES ENTRE RAZONES
TRIGONOMÉTRICAS
Ejercicios:
Calcula las razones trigonométricas restantes:
a) α∈ 1er cuadrante
b) α∈ 4o cuadrante
c) α∈ 3er cuadrante

11. REDUCCIÓN DE LAS RAZONES
TRIGONOMÉTRICAS AL PRIMER CUADRANTE

14. Ángulos complementarios: β = 90º – α