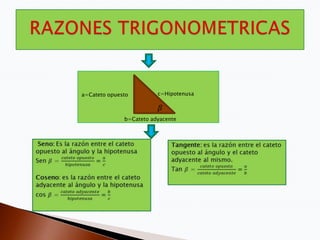
Este documento presenta varios problemas de trigonometría y sus soluciones. Se explican conceptos como las funciones trigonométricas seno, coseno y tangente y cómo se usan para resolver triángulos oblicuángulos. Se resuelven cuatro problemas que involucran hallar lados desconocidos, distancias recorridas, y áreas de triángulos usando propiedades trigonométricas. El documento provee ejemplos prácticos de cómo aplicar conceptos trigonométricos para resolver problemas de la vida real.

2. POR MEDIO DE DIAPOSITIVAS QUEREMOS MOSTRAR
LAS DIFERENTES RAZONES TRIGONOMETRICAS CON
SUS RESPECTIVAS APLICACIONES A LA VIDA REAL
CONOCINDOLAS POR DIFERENTES TIPOS DE
PROBLEMAS QUE SE SOLUCIONAN EN ESTE TRABAJO.

3. a=Cateto opuesto c=Hipotenusa
b=Cateto adyacente

4. c=Hipotenusa

5.  Encontrar el valor de x.
11cm
42°
x
Solución es necesario encontrar la longitud del lado adyacente al ángulo de
42°. la longitud de la hipotenusa. La razón trigonométrica que relaciona el lado
adyacente con la hipotenusa es la razón coseno.
cos 42° = x/11
11(cos 42°)= x Multiplica ambos lados por 11.
x= 8.17

6. El sonar de un barco de salvamento localiza los restos de un naufragio
en un ángulo de depresión de 12°. Un buzo es bajado 40 metros hasta
el fondo del mar. ¿Cuánto necesita avanzar el buzo por el fondo para
encontrar los restos del naufragio?
La distancia que el buzo es
bajado (40 m) es la longitud del
lado opuesto al
ángulo de 12°. La distancia que
el buzo necesita avanzar es la
longitud del
lado adyacente al ángulo de
tan 12°= 40/d 12°. Establece la razón
d(tan 12°) = 40 tangente.
d =40/tan 12°
d =188.19
El buzo necesita avanzar aproximadamente 188
metros para llegar a los restos del
naufragio.

7.  Un árbol de hoja perenne está sostenido por un alambre que se
extiende desde 1.5 pies debajo de la parte superior del árbol hasta
una estaca en el suelo. El alambre mide 24 pies de largo y forma un
ángulo de 58° con el suelo. ¿Qué altura tiene el árbol?
La longitud de la hipotenusa está dada, y la
distancia desconocida es la longitud del lado
opuesto al ángulo de 58°. Establece la razón
seno.
sin 58° =x/24
24(sin 58°) = x
20.4 = x
La distancia desde el suelo hasta el punto donde
el alambre se sujeta al árbol es aproximadamente
20.4 pies. Como el alambre se sujeta a 1.5 pies
debajo de la parte superior del árbol, la altura es
aproximadamente:
20.4 +1.5=21.9 pies.

8.  Una avioneta despega de un aeropuerto elevándose con un ángulo
de inclinación de 7°31minutos. A 2km del aeropuerto en línea recta
con la pista hay una torre de 215m de alto. Diga si la avioneta de
estrella con la torre.
h.av
h
d
d
h.av>h
La avioneta no se estrella

9.  La torre Eiffel en su base cuadrangular mide 50m de lado, ¿Cuál es
su altura si una persona que mide 1,8m de estatura al mirar la punta
mide un ángulo de elevación de 85,4°?
Si tan 85,4° = h/25
25tan85,4°= h
h= 310,72m
Altura de la torre= 310,72+1,8= 312,52

10. Un problema de resolución de triángulos oblicuángulos consiste
en hallar tres de sus elementos, lados o ángulos, cuando se
conocen los otros tres (uno de los cuales ha de ser un lado).

11. Se utilizan tres propiedades:

12.  Casos en la resolución de triángulos:

13.  Annie y Sashi están acampando en la Sierra Nevada. Caminan 8 km
desde su campamento base, con un rumbo de 42°. Después del
almuerzo, cambian de dirección con un rumbo de 137° y caminan
otros 5 km.
 a. ¿A qué distancia están Annie y Sashi de su campamento base?

14.  Considera como formada por dos partes, la parte a la izquierda de la
vertical y la parte a la derecha. Usando la Conjetura AIA, la parte a la
izquierda tiene una medida de 42°. Como la parte a la derecha y el
ángulo de 137° son un par lineal, la parte a la derecha tiene una
medida de 43°. Por lo tanto, la medida de es 42° 43°, u 85°. Ahora
usa la Ley de los cosenos.
 r2 82 52 2(8)(5)(cos 85°)
 r 82 52 2(8)(5)(cos 85°)
 r 9.06
 Sashi y Annie están aproximadamente a 9.1 km de su campamento
base.

15.  PROBLEMA 2: Un topógrafo toma las dimensiones de un
terreno, estableciendo también los ángulos que se forman en sus
lados, cual es el área del terreno.
Solución: Puesto que la suma de los ángulos internos es 180o ,
tenemos que C = 180°-35°-21°=124°.
Luego encontramos el lado AC por la ley de los senos:

16. Por lo tanto, el triángulo quedaría así:
Ahora calculamos la altura del triángulo: sen 21° = h/4.84 h = 4.84 sen 21°
h = 1.73.
Por lo tanto, el área del triángulo es: A = (1/2)(7)(1.73) = 6.06 m2.

17.  PROBLEMA 3: Un viajero parte con una velocidad de 90km/h, a los
10minutos se da cuenta de que se ha equivocado de carretera y toma
otra que forma un ángulo de 120° con la anterior, aunque mantiene la
misma velocidad. Calcular a que distancia del punto de partida se
encuentra una vez transcurrida media hora de viaje
x2 =152 + 302 -2*15*30*cos120

19.  PROBLEMA 4: un globo parte desde un punto A hasta un punto B si
en el transcurro del camino se detiene y observa que del punto A
hasta donde se encuentra hay 2630 metros y desde el puto B hasta
donde se ubica el globo hay 1960 metros. Hallar la distancia entre A
y B sabiendo que el Angulo de diferencia entre A y B es de 63°
63° d2 =26302+19602 -2.2630.1960.cos63
2630 m. 1960 m. d2 =10758500-4680460,45
d2 = 6078039,54
d= 2465,36 m.
A d B

20.  PROBLEMA 4: hallar el lado b de un triangulo cuando:
B= 61° C=42° A=? c=30 cm
B
c=30 Sen B/b=sen C/30
b=30*senB/sen C
A C b=30*sen61°/sen42°
b=26,23/0,66
b=39,21 cm

21.  El primer paso para lograr un buen rendimiento
en esta área o en general en todas las demás
materias es tener un alto gradado de
responsabilidad, para obtener buenos resultados
académicamente con esto estamos seguros de
que se logrará un buen resultado.
Complementando lo anterior decimos que se
deben hacer talleres lúdicos siguiendo con
excelentes trabajos como los del blog
tecnológico, que permitan el desarrollo tanto
académico como ético.