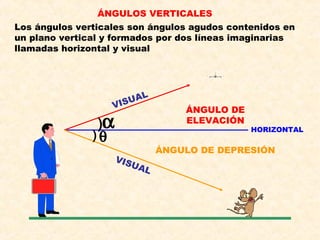
El documento presenta información sobre el teorema de Pitágoras, las razones trigonométricas de ángulos agudos y sus propiedades, la resolución de triángulos rectángulos, el cálculo de áreas de triángulos, ángulos verticales y horizontales, y la determinación de razones trigonométricas de la mitad de un ángulo agudo.

1. RRUUBBÉÉNN AALLVVAA CCAABBRREERRAA

3. TEOREMA DE PITÁGORAS
A
CATETO
HIPOTENUSA
B C
CATETO
(CATETO)2 + (CATETO)2 = (HIPOTENUSA)2
5 4 12 5
3
13
21 29
20

4. RAZONES TRIGONOMÉTRICAS DE
ANGULOS AGUDOS
q
q= CatetoOpuestoa
sen
Hipotenusa
q = q CatetoAdyacentea
cos
Hipotenusa
q =
q
Hipotenusa
sec
CatetoAdyacentea
q = CatetoAdyacentea
q
q =
q
q
Hipotenusa
csc
CatetoOpuestoa
cot
CatetoOpuestoa
q = q
q
CatetoOpuestoa
tan
CatetoAdyacentea
CATETO
OPUESTO
A
CATETO ADYACENTE A q
q
HIPOTENUSA
q
SENO COSENO
TANGENTE COTANGENTE
SECANTE COSECANTE

5. H 12
H2 = 122 + 352
35
TEOREMA DE PITÁGORAS
H = 1369 = 37
senq =
cos q =
tanq = 12
37
35
37
12
35
cot q =
secq =
cscq = 35
12
37
35
37
12
EJEMPLO :
EJEMPLO :
Sabiendo que q es un ángulo agudo tal que senq=2/3.....
3 2
q
q

6. PROPIEDADES DE LAS RAZONES
TRIGOMOMÉTRICAS DE ÁNGULOS AGUDOS
RAZONES TRIGONOMÉTRICAS RECÍPROCAS
sen 1
csc
q =
q
cos 1
sec
q =
q
tan 1
cot
q =
q
senq csc q = 1 cos q secq = 1 tanq cot q = 1
EJEMPLOS
o
A) 1
sen36
B) 1
cos17
= csc36o o
= sec17o
C) tan49o cot49o= 1 D)sen2q csc2q = 1
E)cos63o sec q = 1 q = 63o
F) tan2fcot q = 1 2f = q

7. PROPIEDADES DE LAS RAZONES
TRIGOMOMÉTRICAS DE ÁNGULOS AGUDOS
RAZONES TRIGONOMÉTRICAS DE ÁNGULOS COMPLEMENTARIOS
PROPIEDAD :
“LAS RAZONES TRIGONOMÉTRICAS DE TODO ÁNGULO AGUDO
SON RESPECTIVAMENTE IGUALES A LAS CO-RAZONES
TRIGONOMÉTRICAS DE SU ÁNGULO COMPLEMENTARIO”
A LAS RAZONES TRIGONOMÉTRICAS SENO Y COSENO
TANGENTE Y COTANGENTE ;SECANTE Y COSECANTE
SE LES DENOMINA :CO-RAZONES TRIGONOMÉTRICAS
f senq = cos f
b c
q
cos q =
tanq =
senf
cot f
a
cot q =
secq =
cscq =
tanf
cscf
secf

8. EJEMPLOS
A)sen25o =
B) tan43o =
C)sec60o =
cos65o
cot47o
csc30o
...............
...............
...............
25o + 65o = 90O
43o + 47o = 90O
60o + 30o = 90O
D)senq = cos20o
q + 20o = 90O q = 70o
E) tan5a = cota
5a + a = 90o a = 15o
F)sen
æ p ö çè = cos 5
ø¸ q
5 2
q + p = p
q = p - p
2 5
3 rad
10
q = p

9. TRIÁNGULOS NOTABLES
)
60O 1
1 2
3
30o(
2
45o
1
45o
(
)
3
4
5
37o
53o
(
)
sen30o = 1
2
tan60o = 3
sec 45o = 2 cot 37o = 4
3
tan30o = 1
3
x 3
3
3
3
=
sen45o = 1
2
x 2
2
2
2
=

10. 3 3
o 37 o 45q
)
)
(
(
30o
4 3
4
3 3
CALCULAR : cot q
8 cot 3 3
4
q =

11. RESOLUCIÓN DE TRIÁNGULOS RECTÁNGULOS
CASO 1 : DATOS , HIPOTENUSA y ÁNGULO AGUDO q
q
CASO 2 : DATOS ; CATETO ADYACENTE Y ÁNGULO AGUDOq
q
H Hsenq
Hcos q
Lsecq
L tanq
L
5
62o
5sen62o
5cos62o
8secb 8tanb
8
b

12. CASO 3 : DATOS; CATETO OPUESTO y ÁNGULO AGUDOq
L
Lcsc q k
q
Lcot q
k csc24o
24o
k cot24o
EJEMPLO
a
) q
)
m
Calcular L en términos
de m;a y q
L

13. SOLUCIÓN
a
q
m
L mtana
L mtan
+ a = cot q L + mtana = mcot q
m
L = mcot q -mtana L = m(cot q - tana)
NOTA : DESCOMPOSICIÓN DE UN VECTOR
F
a
y F
x F X
Y
x F = Fcos a
y F = Fsena

14. ÁREA DEL TRIÁNGULO
C
b a
A B
c
S ab senC
=
2
S bc senA
=
2
S ac senB
2
=
EJEMPLO
5m
8m
60O
S (5)(8) sen60o
2
=
S (5)(8) ( 3 )
= = 10 3m2
2 2

15. ÁNGULOS VERTICALES
Los ángulos verticales son ángulos agudos contenidos en
un plano vertical y formados por dos líneas imaginarias
llamadas horizontal y visual
a
q
ÁNGULO DE
ELEVACIÓN
HORIZONTAL
ÁNGULO DE DEPRESIÓN
VISUAL
VISUAL
)
)

16. EJEMPLO :
Una persona observa en un mismo plano vertical dos ovnis
volando a una misma altura con ángulos de elevación de
530 y 370 si la distancia entre los ovnis es de 70m ¿A qué
altura están los ovnis?
SOLUCIÓN
)) o 37
70
12k 12k ) O 53
9k
) 16k
+
9k +70 = 16k k = 10 H = 120
=H

17. ÁNGULOS HORIZONTALES
Los ángulos horizontales son ángulos agudos contenidos en
un plano horizontal, se determinan tomando como
referencia los puntos cardinales norte(N) , sur(S) , este(E) y
oeste(O).
DIRECCIÓN
La dirección de B respecto de A
es N30oE E60oN
La dirección de C respecto de A
es
o
o
S56oO O34oS
RUMBO
El rumbo de Q respecto de P
47o
al oeste del norte
El rumbo de M respecto de P
27o al este del sur
N
O E
S
30O
56O
A
B
C
N
O E
P
S
Q
47o
27o
M
) (
( )

18. ROSA NÁUTICA
Gráfico que contiene 32 direcciones notables, cada dirección
forma entre ellas un ángulo cuya medida es 11o15'
En el gráfico adjunto sólo se muestran 16 direcciones notables,
cada una forma entre ellas un ángulo cuya medida es 22o30'
N
NO NE
O E
SO SE
S
NNE
ENE
NNO
ONO
OSO
SSO
ESE
SSE

19. Las otras 16 direcciones se obtienen trazando las bisectrices de
los 16 ángulos que se muestran en el gráfico anterior.
NE1 4E
E
NE
N
NNE
ENE
E1 4NE
N1 4NE
NE1 4N
N1 4NO
NNO
NO1 4N
NO1 4O NO
ONO
O1 4NO
O
¿Cuánto mide el ángulo entre las direcciones
NE1/ 4N y NO1/ 4O?
Rpta. 90o

20. EJEMPLO :
Un insecto parte de un punto F y recorre 40 km en la dirección
N530O luego recorre 402 km en la dirección SO, finalmente
recorre 60 km hacia el este. ¿A qué distancia se encuentra el
insecto de F ?
SOLUCIÓN N
53o )
37o
O E
S
45o
45o
40
40 2
60
x
24
16 32
40 20 12
16
OBSERVA QUE EL
TRIÁNGULO DE COLOR
ROJO ES NOTABLE
X = 20
F

21. RAZONES TRIGONOMÉTRICAS DE LA MITAD DE UN
ÁNGULO AGUDO (método gráfico)
2 q
q
2
q
c b
a
c )
)
(
) q 2
tan
æ q ö çè ø¸
= 2
b
c a
=
+
c -
a
b
+

22. EJEMPLO :
Sabiendo que : tan 8q=24/7, calcula tan2q
SOLUCIÓN
8q
24
7
25
4q
25
tan4 24
25 7
q =
+
tan4 24
32
q =
tan4 3
4
q =
tan2 3
q = tan2 1
4q 2q
3
4
5
5
9
3
q =
(