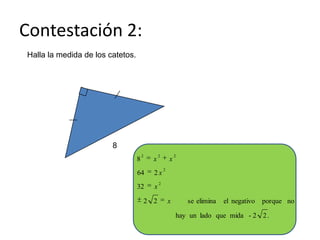
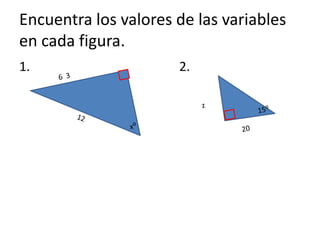
El documento presenta información sobre triángulos rectángulos. Explica la relación entre los lados de un triángulo rectángulo usando el Teorema de Pitágoras. También cubre conceptos como triángulos rectángulos semejantes y relaciones entre los ángulos y lados de triángulos rectángulos con ángulos de 45°, 60° y 90°. Finalmente, presenta ejercicios para practicar el uso de estas propiedades para calcular lados desconocidos.

1. TriángulosRectángulosProf. Carmen BatizUGHS

2. Llena la tablasiguiente con la informaciónque se teofrecerámásadelante.

3. BADC

4. 1. ¿Quépuedesobservar de los resultados de la tabla? 2. ¿Quépuedesconcluir en cuanto a la relaciónquetienen los lados de de un triángulorectángulo ?

5. Teorema de Pitágorasa2 + b2 = c2En un triángulo rectángulo, la suma de los cuadrados de los lados es igual al cuadrado de la hipotenusa

6. El tamaño de un televisorrectángulares dado por la diagonal de de la pantalla. ¿Cuáles el tamaño de la pantalla? 16.2 “ 21.6”

7. La altura de un rectángulomide 21.6 y suanchomide 16.2. Halla la diagonal del rectángulo.a²+ b²= c²16.2 “ (16.2)2 + (21.6) = c² 26 2.44 + 466.56 = c² 729 = c² 21.6” c = 27

8. La diagonal de un rectángulomide 20”. Un lado del rectángulomide 12 “. Halla la medida del otrolado del rectánglo.

9. La diagonal de un rectángulomide 20”. Un lado del rectángulomide 12 “. Halla la medida del otrolado del rectánglo.a² + b²= c²(12²+ b²= (20) ²+ b²= 400b²= 400 – 144b²= 256 b = 1612”20”

10. Los lados de un tríangulo son dados. Determinasiéstosforman un triángulorectángulo. 15, 25, 208, 13, 10

11. Los lados de un tríangulo son dados. Determinasiéstosforman un triángulorectángulo. 15, 25, 208, 13, 10 a2 + b2 = c2 (15)²+ (20) ²= (25) ² 225 + 400 = 625 625 = 625(8) ²+ (10) ²= (13) ² 64 + 100 = 169 164 ≠ 169

12. Teorema de triángulosrectángulossemejantesSi la altura esta trazada en la hipotenusa de un triángulo rectángulo, entonces los dos ángulos formados son semejantes a la figura del triángulo original y a cada otra.C∆ABC ~ ∆ACD ~∆CBDABD

13. Teorema de triángulosrectángulossemejantesEn el ∆ ABC , AB es la hipotenusa y los lados son AC y CB.En el ∆ ACD , AC es la hipotenusa y los lados son CD y AD.En el ∆ ACD , CB es la hipotenusa y los lados son CD y DB.CABD

14. Teorema de triángulosrectángulossemejantesPor lo tanto cada uno de éstos lados son correspondientes y se pueden expresar como: Si ∆ ABC ~ ∆ CBD, entonces AB = CB BC BDCABD

15. Ejemplos: Completa: 1. QS = ? RS PS 2. QS = ? QR QP 3. RQ = PR RS ?PSQR

16. contestaciones: Completa: 1. QS = ? RS RS PS 2. QS = ? PR QR QP 3. RQ = PRRS RS ?PSQR

17. ∆MNQ, XY es la altura de la hipotenusa de MN. Identifica los triángulossemejantes.MYNX

18. ∆MNX, XY es la altura de la hipotenusa de MN. Identifica los triángulossemejantes.MY∆ MNX ~ ∆MXY ~ ∆NXYNX

19. EjercicioLedabcNMPUtiliza el diagramaparacompletarcadaproporción.b = a 2. b + c = d a ? d ?? = e 4. d = b + c e c ? a

20. ContestacionesLedabcNMPUtiliza el diagramaparacompletarcadaproporción.b = a 2. b + c = d a ? d ?? = d 4. d = b + c e c ? ab + cceb

21. Encuentra la medida de x, y y zA6Dy10xzBc

22. Encuentra la medida de x, y y zA6Dy10x∆ABC ~ ∆ACD ~ ∆BCDPOR LO TANTO:AB = AC16 = Y Y²= 96 AC AD Y 6 Y = = (6) ²+ X²= 96+ X²= 96X²= 96- 36X = 60zBcX2 + (10) ²= Z²60 + 100 = Z² = Z²Z = =

23. Utiliza el diagramaparahallar AO, OC.yCAxO

24. Utiliza el diagramaparahallar AO, OC.yCAO = 10 unidadesEn cambio OC se busca con la f’ormula de distancia:AxO

25. Halla la distancia entre los puntos (-4,6) y ( 0,3)

26. Halla la distancia entre los puntos (-4,6) y ( 0,3)5 = ( x₂ – x₁)² + (y₂–y₁) 2 = (0-(-4)²+ (3 -6) ² = 16 + 9 = 85

27. Relaciones de TriángulosRectángulosTriángulo 45⁰- 45⁰- 90⁰en estecaso el triánguloesisósceles.Triángulo 30⁰-60⁰-90⁰45⁰a45⁰a30⁰2a60⁰a

28. 45º,45º, 90ºSi los dos ángulos de un triángulo rectángulo rectángulo miden 45º, entonces la hipotenusa mide veces la medida de sus lados.45ºa45ºa

29. EJEMPLO 1:Halla la medida de la hipotenusa.45º1045º10

30. Contestación 1:Halla la medida de la hipotenusa.45º1045º10

31. EJEMPLO 2:Halla la medida de los catetos.8

32. Contestación 2:Halla la medida de los catetos.8

33. 30º,60º, 90ºSi los dos ángulos de un triángulo rectángulo miden 30º y 60º entonces la hipotenusa mide dos veces la medida del lado corto y la medida del otro lado es veces la medida del lado corto.30ºa2a60º

34. Ejercicio 3Halla la medida de los catetos.30º1560º

35. Contestación 3Halla la medida de los catetos.El lado más corto es la mitad de la hipotenusa.30º7.515El lado más largo es veces el lado corto. 60º

36. Ejercicio 4Halla la medida de el cateto y la hipotenusa.830º60º

37. Contestación 4:Halla la medida de el cateto y la hipotenusa.830ºLa hipotenusa es el doble del lado corto, que es 8. Por lo tanto la hipotenusa mide 16.1660ºEl otro lado es veces el lado corto.

38. Halla la medida exacta deconocida de cadalado del triangulo. 2.3. 4. AE5 245⁰7DBCFQB60⁰60⁰530⁰P30⁰AC7R

39. Halla la medida exacta deconocida de cadalado del triángulo. 2.3. 4. AE45⁰7DBCFQB60⁰60⁰530⁰P30⁰AC7R

40. TRIGONOMETRÍAsen A = opuestohipotenusacos A = adyacentehipotenusa tan A = opuestoadyacentePara recordarte: sohcahtoaBAC

41. Encuentra los valores de las variables en cadafigura.1. 2. 6 3z15⁰12x⁰20

42. Encuentra los valores de las variables en cadafigura.1. 2. 6 3z15⁰12x⁰20La informaciónqueestandandoesopuesto e hipotenusapor lo tantoutilizaremos:sen x = 6 3 = 3 12 2 x = 60⁰La informaciónqueestandandoesadyacente y opuestopor lo tantoutilizaremos: tan 15⁰ = 20 = z z = 20 tan 15⁰ z ≈ 5.4