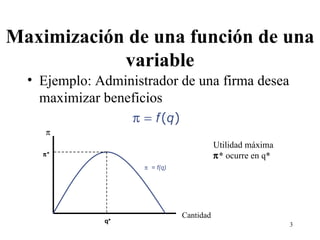
Este documento presenta los conceptos matemáticos básicos de la optimización, incluida la maximización de funciones de una y múltiples variables, derivadas parciales, condiciones de primer y segundo orden, y el teorema de la envolvente. Proporciona ejemplos para ilustrar cómo se aplican estos conceptos para resolver problemas de maximización en economía.





































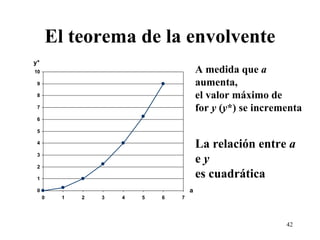







![El teorema de la envolvente Sustituyendo en la función objectivo original resulta en una expresión para el valor óptimo de y ( y *) y * = f [ x 1 *( a ), x 2 *( a ),…, x n *( a ), a ] Diferenciando resulta](https://image.slidesharecdn.com/modulo1-100520110721-phpapp01/85/Modulo-1-Analisis-Matematico-de-la-Optimizacion-50-320.jpg)























![Restricciones de desigualdad Podemos establecer el siguente Lagrangiano L = f ( x 1 , x 2 ) + 1 [ g ( x 1 , x 2 ) - a 2 ] + 2 [ x 1 - b 2 ] + 3 [ x 2 - c 2 ] Con lo cual obtendremos ocho condiciones de primer orden](https://image.slidesharecdn.com/modulo1-100520110721-phpapp01/85/Modulo-1-Analisis-Matematico-de-la-Optimizacion-74-320.jpg)















![Maximización restringida Combinando términos y reordenando d 2 y = f 11 f 2 2 - 2 f 12 f 1 f 2 + f 22 f 1 2 [ dx 1 2 / f 2 2 ] Por lo tanto, para d 2 y < 0, debe ser cierto que f 11 f 2 2 - 2 f 12 f 1 f 2 + f 22 f 1 2 < 0 Esta ecuación caracteriza un conjunto de funciones denominadas funciones cuasi-cóncavas cualquier par de puntos dentro del conjunto puede formar una línea introducida completamente en el conjunto](https://image.slidesharecdn.com/modulo1-100520110721-phpapp01/85/Modulo-1-Analisis-Matematico-de-la-Optimizacion-90-320.jpg)



















