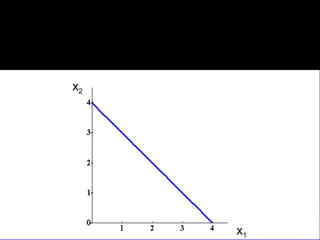
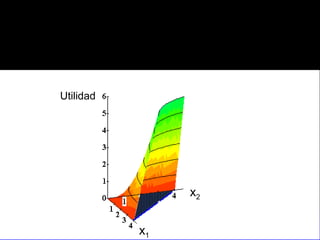
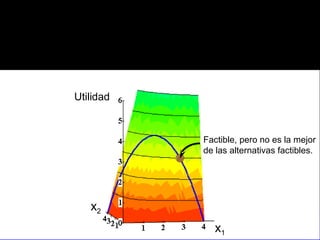
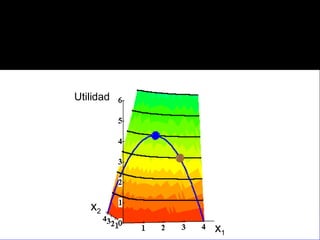
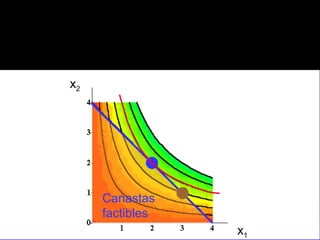
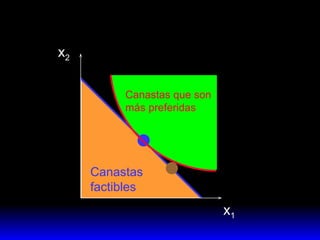
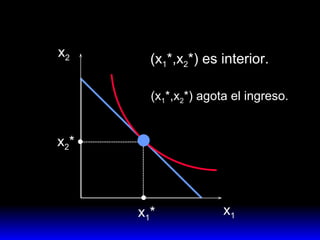
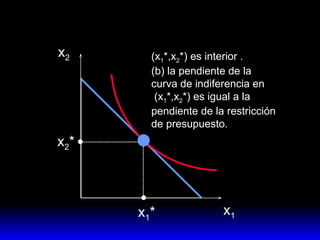
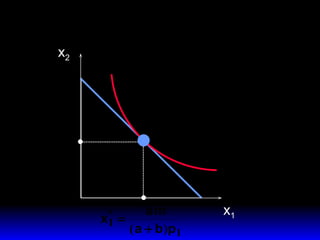
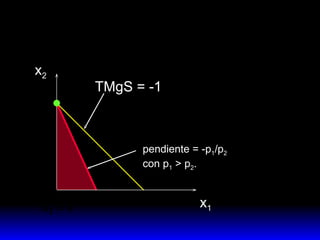
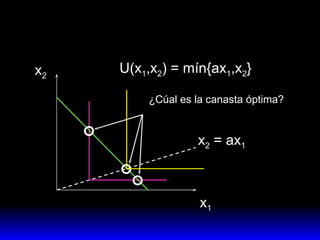
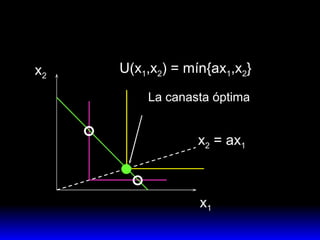
El documento explica los conceptos fundamentales de la demanda del consumidor racional. Indica que el consumidor elige la mejor canasta de bienes de su conjunto de opciones factibles, considerando sus preferencias y restricción presupuestaria. La mejor canasta se conoce como demanda ordinaria y puede ser una solución interior o de esquina, dependiendo de la forma de las curvas de indiferencia y la pendiente de la restricción.

1. Capítulo 5 Óptimo del Consumidor

2. Racionalidad Económica El principal postulado acerca del comportamiento del consumidor dice que escoje la mejor alternativa del conjunto de alternativas factibles. Las alternativas disponibles constituyen el conjunto factible. ¿Cuál es la mejor canasta del conjunto factible?

3. x 1 x 2

4. x 1 x 2 Utilidad

5. Utilidad x 2 x 1

6. x 1 x 2 Utilidad

7. Utilidad x 1 x 2

8. Utilidad x 1 x 2

9. Utilidad x 1 x 2

10. Utilidad x 1 x 2

11. Utilidad x 1 x 2 Factible, pero no es la mejor de las alternativas factibles.

12. x 1 x 2 Utilidad La mejor de las canastas factibles Factible, pero no es la mejor de las alternativas factibles.

13. x 1 x 2 Utilidad

14. Utilidad x 1 x 2

15. Utilidad x 1 x 2

16. Utilidad x 1 x 2

17. x 1 x 2

18. x 1 x 2 Canastas factibles

19. x 1 x 2 Canastas factibles

20. x 1 x 2 Canastas que son más preferidas Canastas factibles

21. x 1 x 2 Canastas factibles Canastas que son más preferidas

22. x 1 x 2 x 1 * x 2 *

23. x 1 x 2 x 1 * x 2 * (x 1 *,x 2 *) es la mejor De las canasta factibles.

24. La mejor de las canastas factibles es conocida como la DEMANDA ORDINARIA a los precios y el ingreso dados. La demanda ordinaria se denota por x 1 *(p 1 ,p 2 ,m) y x 2 *(p 1 ,p 2 ,m).

25. Cuando x 1 * > 0 y x 2 * > 0 la canasta demandada es INTERIOR . Si se compra (x 1 *,x 2 *) el costo es m entonces se agota el ingreso.

26. x 1 x 2 x 1 * x 2 * (x 1 *,x 2 *) es interior. (x 1 *,x 2 *) agota el ingreso.

27. x 1 x 2 x 1 * x 2 * (x 1 *,x 2 *) es interior. (a) (x 1 *,x 2 *) agota el ingreso: p 1 x 1 * + p 2 x 2 * = m.

28. x 1 x 2 x 1 * x 2 * (x 1 *,x 2 *) es interior . (b) la pendiente de la curva de indiferencia en (x 1 *,x 2 *) es igual a la pendiente de la restricción de presupuesto.

29. (x 1 *,x 2 *) satisface dos condiciones: (a) el ingreso se agota: p 1 x 1 * + p 2 x 2 * = m (b) la pendiente de la restricción de presupuesto, -p 1 /p 2 , y la pendiente de la curva de indiferencia que contiene a (x 1 *,x 2 *) son iguales en (x 1 *,x 2 *).

30. Estimando la Demanda Ordinaria ¿Cómo podemos emplear esta información para poder encontrar la canasta (x 1 *,x 2 *) para los precios p 1 , p 2 y el ingreso m?

31. Estimando la demanda ordinara. Ejemplo para una Cobb Douglas Supongamos que las preferencias del consumidor son del tipo Cobb-Douglas.

32. En consecuencia:

33. Y la TMgS:

34. En (x 1 *,x 2 *), se debe cumplir que TMgS = -p 1 /p 2 , en consecuencia

35. (A)

36. Y sabemos que (x 1 *,x 2 *) agota el presupuesto del consumidor: (B)

37. En consecuencia, sabemos que: (A) (B)

38. (A) (B) Sustituyendo

39. (A) (B) y tenemos: y simplificando ….

41. y sustituyendo este valor de x 1 * en Obtenemos:

43. Así hemos descubierto que la mejor canasta factible para el consumidor con preferencias Cobb-Douglas es

44. x 1 x 2

45. Restricciones para el óptimo del consumidor Cuando x 1 * > 0 y x 2 * > 0 y (x 1 *,x 2 *) agota el ingreso, y la curva de indiferencia tiene una forma regular, no especial , la demanda ordinaria se obtiene mediante: (a) p 1 x 1 * + p 2 x 2 * = m (b) la pendiente de la restricción de presupuesto, -p 1 /p 2 , y la pendiente de la curva de indiferencia en la canasta (x 1 *,x 2 *) son iguales.

46. ¿Pero, y si x 1 * = 0? ¿Pero y si x 2 * = 0? Si x 1 * = 0 ó x 2 * = 0 entonces la demanda ordinaria (x 1 *,x 2 *) es una solución de esquina .

47. Ejemplo de soluciones de esquina – el caso de sustitutos perfectos x 1 x 2 TMgS = -1

48. x 1 x 2 pendiente = -p 1 /p 2 con p 1 > p 2 . TMgS = -1

49. x 1 x 2 TMgS = -1 pendiente = -p 1 /p 2 con p 1 > p 2 .

50. x 1 x 2 TMgS = -1 pendiente = -p 1 /p 2 con p 1 > p 2 .

51. x 1 x 2 pendiente = -p 1 /p 2 con p 1 < p 2 . TMgS = -1

52. En consecuencia, si la función de utilidad es = x 1 + x 2 , la canasta óptima es (x 1 *,x 2 *) donde: y si p 1 < p 2 si p 1 > p 2 .

53. x 1 x 2 TMgS = -1 pendiente = -p 1 /p 2 con p 1 = p 2 .

54. x 1 x 2 Todas las canastas en la restricción de presupuesto son canastas óptimas si p 1 = p 2 .

55. Ejemplo de soluciones de esquina – el caso de las preferencias no convexas x 1 x 2 mejor

56. x 1 x 2

57. x 1 x 2 ¿Cuál es la canasta óptima?

58. x 1 x 2 La canasta óptima

59. x 1 x 2 Observe que la solución de tangencia no es la canasta óptima. La canasta óptima

60. Ejemplos de soluciones en “punta” – el caso de complementarios perfectos x 1 x 2 U(x 1 ,x 2 ) = mín{ax 1 ,x 2 } x 2 = ax 1

61. x 1 x 2 TMgS = 0 U(x 1 ,x 2 ) = mín{ax 1 ,x 2 } x 2 = ax 1

62. x 1 x 2 TMgS = -  TMgS = 0 U(x 1 ,x 2 ) = mín{ax 1 ,x 2 } x 2 = ax 1

63. x 1 x 2 TMgS es indefinida U(x 1 ,x 2 ) = mín{ax 1 ,x 2 } x 2 = ax 1 TMgS = -  TMgS = 0

64. x 1 x 2 U(x 1 ,x 2 ) = mín{ax 1 ,x 2 } x 2 = ax 1

65. x 1 x 2 U(x 1 ,x 2 ) = mín{ax 1 ,x 2 } x 2 = ax 1 ¿Cúal es la canasta óptima?

66. x 1 x 2 U(x 1 ,x 2 ) = mín{ax 1 ,x 2 } x 2 = ax 1 La canasta óptima

67. x 1 x 2 U(x 1 ,x 2 ) = mín{ax 1 ,x 2 } x 2 = ax 1 x 1 * x 2 *

68. x 1 x 2 U(x 1 ,x 2 ) = mín{ax 1 ,x 2 } x 2 = ax 1 x 1 * x 2 * (a) p 1 x 1 * + p 2 x 2 * = m

69. x 1 x 2 U(x 1 ,x 2 ) = mín{ax 1 ,x 2 } x 2 = ax 1 x 1 * x 2 * (a) p 1 x 1 * + p 2 x 2 * = m (b) x 2 * = ax 1 *

70. (a) p 1 x 1 * + p 2 x 2 * = m; (b) x 2 * = ax 1 *.

71. (a) p 1 x 1 * + p 2 x 2 * = m; (b) x 2 * = ax 1 *. Substituyendo, tenemos p 1 x 1 * + p 2 ax 1 * = m

73. Y sustituyendo este resultado para obtener x 2 *:

74. x 1 x 2 U(x 1 ,x 2 ) = mín{ax 1 ,x 2 } x 2 = ax 1