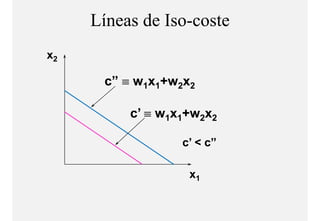
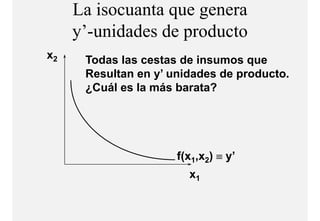
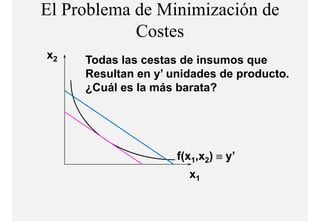
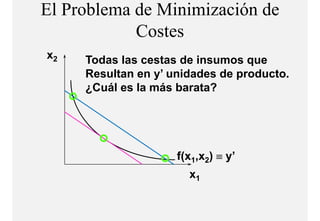
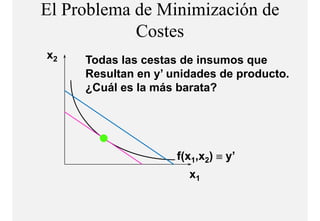
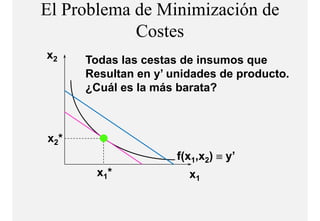
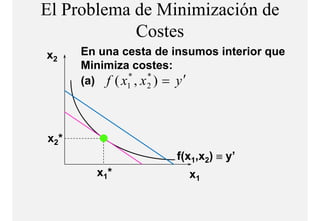
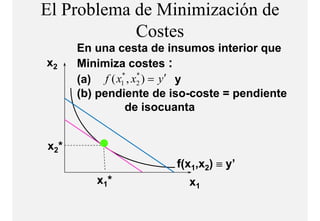
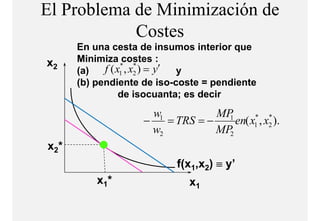
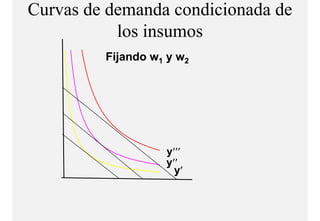
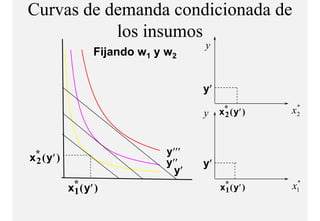
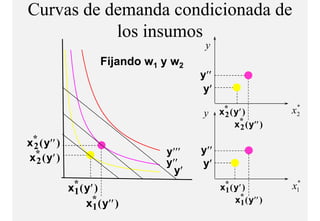
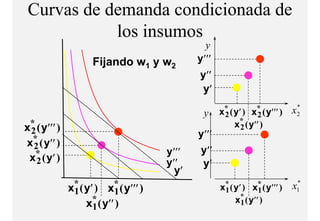
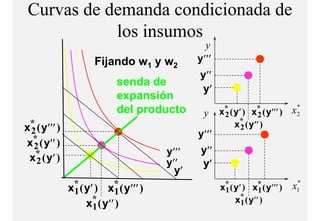
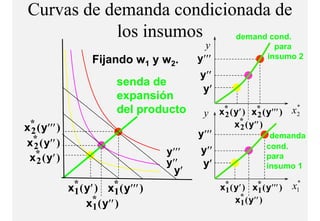
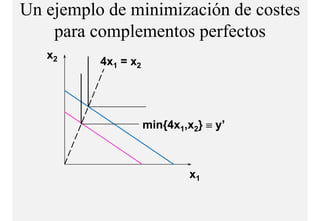
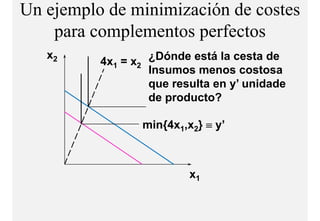
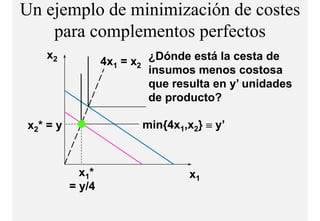
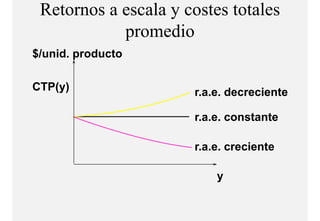
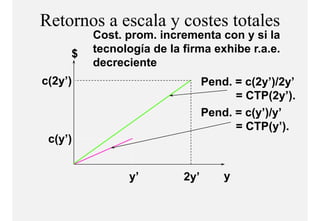
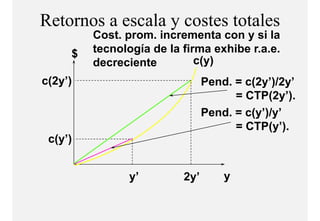
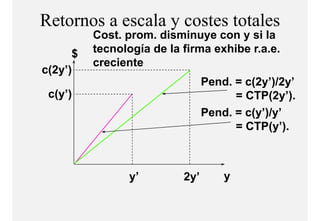
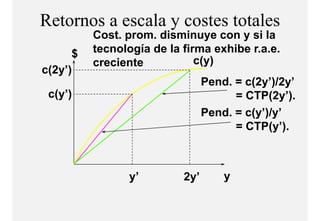
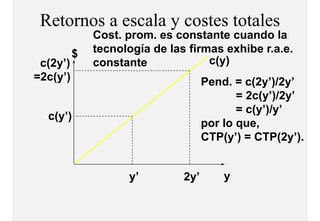
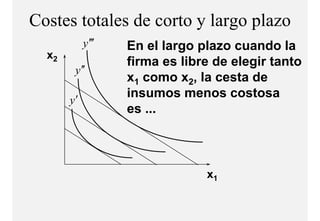
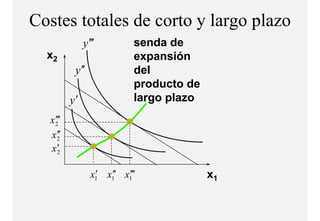
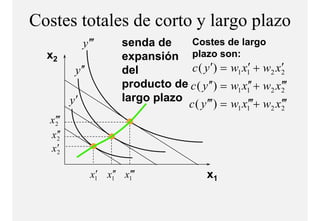
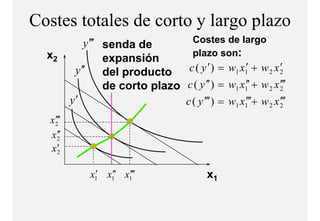
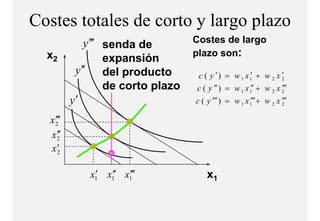
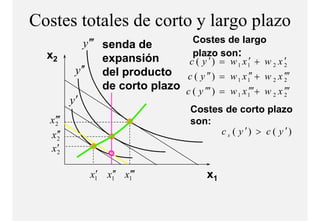
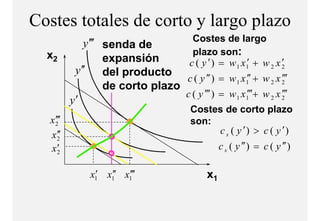
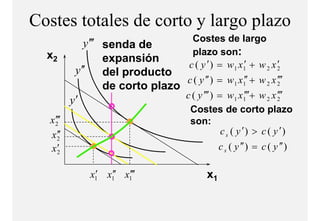
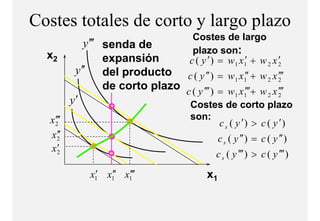
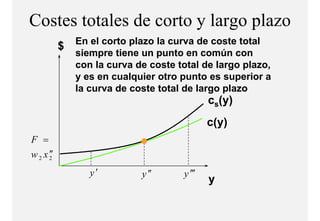
El documento describe el problema de minimización de costos para una firma. Explica que la firma busca producir cada nivel de producción al menor costo total posible. Se define la función de costo total y se describe el problema matemático de minimización sujeto a la función de producción. Finalmente, se presenta un ejemplo numérico con una función Cobb-Douglas para ilustrar cómo se derivan las curvas de demanda condicional de los insumos.

1. Módulo 9
Costos de Producción

2. Minimización de costes
Una firma es minimizadora de costos
si ésta produce cualquier nivel de
producto y ≥ 0 al menor costo total.
c(y) denota el costo total más
pequeño posible de la firma para
producir y unidades de producto
producto.
c(y) es la fución de costo total de la
firma.

3. Minimización de costes
Cuando la firma enfrenta los precios
de los insumos w = (w1,w2,…,wn) la
función total de gasto será
f ó á
c(w1,…,wn,y).
( y)

4. El Problema de Minimización de
Costes
C t
Consideremos una firma que utiliza dos
insumos para producir
La f
L función de producción es
ió d d ió
y = f(x1,x2)
Tomamos como dado el nivel de producto
y≥0
Dado los precios de los insumos w1 y w2,
el coste de una cesta de insumos (x1,x2)
(
es
w1x1 + w2x2

5. El Problema de Minimización de
Costes
C t
Para dados w1, w2 e y el problema de
y,
minimización de costes de la firma
es
min w1 x1 + w 2 x 2
x1 , x 2 ≥ 0
sujeta a f ( x1 , x 2 ) = y .

6. El Problema de Minimización de
Costes
C t
Los niveles x1*(w1,w2,y) y x1*(w1,w2,y)
w y) w y)
en la cesta de insumos menos
costosos son las demandas
condicionales para los insumos 1 y 2
p
El (más pequeño) coste total posible
para producir y unidades es
c ( w1 , w 2 , y ) = w x ( w1 , w 2 , y )
*
1 1
+ w 2 x ( w1 , w 2 , y ).
*
2

7. Demandas de insumo condicional
Dados w1, w2 e y ¿cómo se halla la
y,
cesta de insumos menos costoso?
¿Y cómo se computa la función de
coste total?

8. Líneas de Iso-coste
Una curva que contiene todas las
cestas de insumo que cuestan la
misma cantidad es una curva de iso-
coste
Ej., dado w1 y w2, la línea de iso-
coste $100 tiene la ecuación
w1 x1 + w2 x2 = 100.

9. Líneas de Iso-coste
Generalmente,
Generalmente dado w1 y w2, la
ecuación de isocostes $c es
w1 x1 + w 2 x 2 = c
es decir,
w1 c
x2 = − x1 + .
w2 w2
La
L pendiente es - w1/ 2.
di t /w

10. Líneas de Iso-coste
x2
c” ≡ w1x1+w2x2
c
c’ ≡ w1x1+ 2x2
’ +w
c’ < c”
’ ”
x1

11. Líneas de Iso-coste
x2 pendientes = -w1/w2.
w
c” ≡ w1x1+w2x2
c
c’ ≡ w1x1+ 2x2
’ +w
c’ < c”
’ ”
x1

12. La isocuanta que genera
y’-unidades de producto
’ id d d d t
x2 Todas las cestas de insumos que
Resultan en y’ unidades de producto.
¿Cuál es la más barata?
f(x1,x2) ≡ y’
x1

13. El Problema de Minimización de
Costes
C t
x2 Todas las cestas de insumos que
Resultan en y’ unidades de producto.
¿Cuál es la más barata?
f(x1,x2) ≡ y’
x1

14. El Problema de Minimización de
Costes
C t
x2 Todas las cestas de insumos que
Resultan en y’ unidades de producto.
¿Cuál es la más barata?
f(x1,x2) ≡ y’
x1

15. El Problema de Minimización de
Costes
C t
x2 Todas las cestas de insumos que
Resultan en y’ unidades de producto.
¿Cuál es la más barata?
f(x1,x2) ≡ y’
x1

16. El Problema de Minimización de
Costes
C t
x2 Todas las cestas de insumos que
Resultan en y’ unidades de producto.
¿Cuál es la más barata?
x 2*
f(x1,x2) ≡ y’
x 1* x1

17. El Problema de Minimización de
Costes
C t
x2 En una cesta de insumos interior que
Minimiza costes:
(a) f ( x1 , x 2 ) = y ′
* *
x 2*
f(x1,x2) ≡ y’
x 1* x1

18. El Problema de Minimización de
Costes
C t
En una cesta de insumos interior que
x2 Minimiza costes :
(a) f ( x1 , x2 ) = y′ y
* *
(b) pendiente de iso-coste = pendiente
de isocuanta
x 2*
f(x1,x2) ≡ y’
x y
x 1* x1

19. El Problema de Minimización de
Costes
C t
En una cesta de insumos interior que
x2 Minimiza
Mi i i costes : t
(a) f ( x1 , x2 ) = y′ y
* *
(b) pendiente de iso-coste = pendiente
de isocuanta; es decir
w1 MP
− = TRS = − 1 en( x1 , x2 ).
* *
w2 MP2
x 2*
f(x1,x2) ≡ y’
x y
x 1* x1

20. Un Ejemplo Cobb-Douglas de
Minimización d C t
Mi i i ió de Costes
La función de producción Cobb-
Cobb
Douglas de una firma es
y = f ( x1, x2 ) = x x .
1/ 3 2 / 3
1 2
Los precios de los insumos son w1 y
w 2.
¿Cuáles son l f
C ál las funciones de
i d
demanda condicional de los
insumos?

21. Un Ejemplo Cobb-Douglas de
Minimización d C t
Mi i i ió de Costes
En la cesta de insumos (x1*,x2*) que minimiza
el coste de producir y unidades de producto:
p p
(a) y = (x ) (x )
* 1/ 3
1
* 2/3
2 y
(b) w1 ∂ y / ∂ x1 * −2 / 3
(1 / 3)( x ) ( x ) * 2/3
− =− =− 1 2
w2 ∂ y / ∂ x2 * 1/ 3
(2 / 3)( x ) ( x )
1
* −1 / 3
2
*
x
=− 2
.*
2x 1

22. Un Ejemplo Cobb-Douglas de
Minimización d C t
Mi i i ió de Costes
*
w1 x2
( ) y = (x ) (x )
(a) * 1/ 3
1
* 2/3
2 (b) w = 2 x * .
2 1

23. Un Ejemplo Cobb-Douglas de
Minimización d C t
Mi i i ió de Costes
*
w1 x2
y = ( x1* )1 / 3 ( x 2 ) 2 / 3 (b) w = 2 x * .
*
(a)
( )
2 1
2 w1 *
De ( )
(b), x =
*
2 x1 .
w2

24. Un Ejemplo Cobb-Douglas de
Minimización d C t
Mi i i ió de Costes *
w1 x2
y = (x )
* 1/3 *
(x ) 2/3
= .
(a)
( ) 1 2
(b) w 2 2 x1*
2 w1 *
De ( )
(b), x =
*
2 x1 .
w2
Ahora sustituimos en (a) 2y3 tenemos
Ah tit i ( ) / t
* 1 / 3  2 w1 * 
y = ( x1 )   w x1
 2 

25. Un Ejemplo Cobb-Douglas de
Minimización d C t
Mi i i ió de Costes
*
w1 x2
( ) y = (x )
(a)
* 1/3 *
(x ) 2/3
(b) = *
.
1 2
w2 2 x1
2 w1 *
De ( )
(b), x =
*
2 x1 .
w2
Ahora sustituimos en (a) y tenemos
Ah tit i ( ) t
2/3 2/3
 2 w1 *   2 w1 
y = (x )
*
1
1/3

 w x1 = 
 w
*
x .
1
 2   2 

26. Un Ejemplo Cobb-Douglas de
Minimización d C t
Mi i i ió de Costes *
w1 x2
( ) y = (x )
(a)
* 1/3
1 (x ) *
2
2/3
(b) = *
.
w2 2 x1
2 w1 *
De (b),
D (b) x = *
2 x1 .
w2
Ahora sustituimos en (a) y tenemos
2/3 2/3
 2 w1 *   2 w1 
y = (x )
*
1
1/3

 w x1 = 
 w
*
x .
1
 2   2 
2/3
 w2 
Y x = 
*
1  2w 
 y la dda. condicionada
es
 1  para el insumo 1

27. Un Ejemplo Cobb-Douglas de
Minimización d C t
Mi i i ió de Costes
2/ 3
2w1 *  w2 
Dado x =
*
2 x1 y x =
*
1  2w  y
w2  1
2/ 3 1/ 3
2w1  w2   2w1 
x =
*
  y =  y
w2  2w1  w
2
  2
es la demanda condicionada para el insumo 2
p

28. Un Ejemplo Cobb-Douglas de
Minimización d C t
Mi i i ió de Costes
Por lo que la cesta de insumos más barata
que resulta en y unidades de producto es
(x*
1
*
( w1 , w 2 , y ), x 2 ( w1 , w 2 , y ) )
  w  2 / 3  2 w 1 / 3 
=  2
 2w y ,
 w
1
y .
 1   2 
 

29. Curvas de demanda condicionada de
los i
l insumos
Fijando w1 y w2
y′′′
y′′
y′

30. Curvas de demanda condicionada de
los i
l insumos
y
Fijando w1 y w2
y′
*
y x* ( y′ )
2 x2
y′′′
x* ( y′ )
2 y′′ y′
y′
x* ( y′ )
*
1 x* ( y′ )
1 x1

31. Curvas de demanda condicionada de
los i
l insumos
y
Fijando w1 y w2
y′′
y′
*
y x* ( y′ )
2 x2
x* ( y′′ )
2
x* ( y′′ )
2
y′′′ y′′
x* ( y′ )
2 y′′ y′
y′
x* ( y′ )
*
1 x* ( y′ )
1 x1
x* ( y′′ ) x* ( y′′ )
1
1

32. Curvas de demanda condicionada de
los i
l insumos
y
Fijando w1 y w2 y′′′
y′′
y′
*
y x* ( y′ ) x* ( y′′′ )
2 2 x2
x* ( y′′′ ) x* ( y′′ )
2
2 y′′′
x* ( y′′ )
2
y′′′ y′′
x* ( y′ )
2 y′′ y′
y′
x* ( y′ ) x* ( y′′′ )
*
1 1 x* ( y′ ) x* ( y′′′ )
1 1 x1
x* ( y′′ ) x* ( y′′ )
1
1

33. Curvas de demanda condicionada de
los i
l insumos
y
Fijando w1 y w2 y′′′
y′′
senda de
y′
expansión
del producto y x* ( y′ ) x* ( y′′′ )
2 2
*
x2
x* ( y′′′ ) x* ( y′′ )
2
2 y′′′
x* ( y′′ )
2
y′′′ y′′
x* ( y′ )
2 y′′ y′
y′
x* ( y′ ) x* ( y′′′ )
*
1 1 x* ( y′ ) x* ( y′′′ )
1 1 x1
x* ( y′′ ) x* ( y′′ )
1
1

34. Curvas de demanda condicionada de
los i
l insumos demand cond.
y para
Fijando
Fij d w1 y w2. y′′′ insumo 2
y′′
senda de
y′
expansión
del producto y x* ( y′ ) x* ( y′′′ )
2 2
*
x2
x* ( y′′′ ) x* ( y′′ )
2
2 y′′′ demanda
x* ( y′′ )
2 cond.
y′′′ y′′
x* ( y′ )
2 y′′
para
y′ insumo 1
y′
x* ( y′ ) x* ( y′′′ )
*
1 1 x* ( y′ ) x* ( y′′′ )
1 1 x1
x* ( y′′ ) x* ( y′′ )
1
1

35. Un ejemplo Cobb-Douglas de
minimización de costes
i i i ió d t
Para la función de producción
y = f ( x1 , x 2 ) = x1 / 3 x 2 / 3
1 2
la cesta de insumo más barata para obtener
y unidades de producto es
(x*
1
*
( w1 , w 2 , y ), x ( w1 , w 2 , y )
2 )
  w  2 / 3  2 w 1 / 3 
=  2 y , 1
y .
  2 w1   w
  2  

36. Un ejemplo Cobb-Douglas de
minimización de costes
i i i ió d t
La función de coste total de la firma es
c ( w1 , w2 , y ) = w1 x1* ( w1 , w2 , y ) + w2 x 2 ( w1 , w2 , y )
*

37. Un ejemplo Cobb-Douglas de
minimización de costes
i i i ió d t
La función de coste total de la firma es
c ( w 1 , w 2 , y ) = w 1 x1* ( w 1 , w 2 , y ) + w 2 x 2 ( w 1 , w 2 , y )
*
2/3 1/ 3
 w2   2 w1 
 2w 
= w1  y + w2 
 w  y
 1   2 

38. Un ejemplo Cobb-Douglas de
minimización de costes
i i i ió d t
La función de coste total de la firma es
c ( w1 , w 2 , y ) = w1 x1* ( w1 , w 2 , y ) + w 2 x 2 ( w1 , w 2 , y )
*
2/3 1/ 3
 w2   2 w1 
= w1 
 2w y + w2 
 w y
 1   2 
2/3
1
= 1/ 3
w
1 w 2/3
2 y+2 1/ 3 1/ 3
w
1 w 2/3
2 y
2

39. Un ejemplo Cobb-Douglas de
minimización de costes
i i i ió d t
La función de coste total de la firma es
c ( w 1 , w 2 , y ) = w 1 x1* ( w 1 , w 2 , y ) + w 2 x 2 ( w 1 , w 2 , y )
*
2/3 1/3
 w2   2 w1 
= w1 
 2w   w 
y + w2  y
 1   2 
2/3
1
=  w1 / 3 w 2 / 3 y + 2 1 / 3 w1 / 3 w 2 / 3 y
1 2 1 2
2
1/3
 w1 w  2
= 3
 4 
2
y.
 

40. Un ejemplo de minimización de costes
para complementos perfectos
l t f t
La función de producción de la firma
es
y = min{4 x1 , x2}
i { }.
Los precios de los insumos w1 y w2
están dados
¿Cuáles son l d
C ál las demandasd
condicionadas de los insumos 1 y 2?
¿Y el coste total de la firma?

41. Un ejemplo de minimización de costes
para complementos perfectos
l t f t
x2
4x1 = x2
min{4x1,x2} ≡ y’
x1

42. Un ejemplo de minimización de costes
para complementos perfectos
l t f t
x2
4x1 = x2
min{4x1,x2} ≡ y’
x1

43. Un ejemplo de minimización de costes
para complementos perfectos
l t f t
x2
4x1 = x2 ¿Dónde está la cesta de
Insumos menos costosa
que resulta en y’ unidade
y
de producto?
min{4x1,x2} ≡ y’
x1

44. Un ejemplo de minimización de costes
para complementos perfectos
l t f t
x2
4x1 = x2 ¿Dónde está la cesta de
insumos menos costosa
que resulta en y’ unidades
y
de producto?
x 2* = y min{4x1,x2} ≡ y’
x 1* x1
= y/4

45. Un ejemplo de minimización de costes
para complementos perfectos
l t f t
La función de producción de la firma es
y = min{ 4 x1 , x 2 }
y l demandas condicionadas de los
las d d di i d d l
insumos son
y x ( w1 , w 2 , y ) = y .
*
x ( w1 , w 2 , y ) =
*
1 y 2
4

46. Un ejemplo de minimización de costes
para complementos perfectos
l t f t
La función de producción de la firma es
y = min{ 4 x1 , x 2 }
y l demandas condicionadas de los
las d d di i d d l
insumos son
y x 2 ( w1 , w 2 , y ) = y .
*
x1 ( w1 , w 2 , y ) =
*
y
4
Por lo que la función de coste total es
c ( w1 , w 2 , y ) = w1 x1 ( w1 , w 2 , y )
*
+ w 2 x ( w1 , w 2 , y )
*
2

47. Un ejemplo de minimización de costes
para complementos perfectos
l t f t
La función de producción de la firma es
y = min{ 4 x 1 , x 2 }
y las demandas condicionadas de los
insumos son
y x2 ( w1, w 2 , y ) = y.
*
x1 ( w 1 , w 2 , y ) =
*
y
4
Por lo que la función de coste total es
c ( w 1 , w 2 , y ) = w 1 x 1* ( w 1 , w 2 , y )
+ w 2 x ( w1 , w 2 , y )
*
2
y  w1 
= w1 + w 2 y =  + w2 y.
4  4 

48. Coste total promedio
p
Para niveles de producto positivos,
P i l d d t iti
el coste total promedio de la firma de
producir y unidades es
c ( w1 , w2 , y )
AC ( w1 , w2 , y ) = .
y

49. Retornos a escala y costes totales
promedio
di
Las propiedades de los retornos a escala de
la tecnología de una firma determina cómo
cambia los costes de producción promedio
cuando cambia el nivel de producto
Nuestra fi
N t firma produce actualmente y’
d t l t ’
unidades de procucto
¿Cómo cambia el coste de producción
promedio de la firma si produce 2y’
unidades de producto?

50. Retornos constantes a escala y costes
totales
t t l promediodi
Si la tecnología de una firma exhibe
retornos constantes a escala
entonces duplicando su nivel de
p
producto de y’ a 2y’ requiere
y y q
duplicar todos los niveles de
insumos

51. Retornos constantes a escala y costes
totales
t t l promediodi
Si la tecnología de una firma exhibe
retornos constantes a escala entonces
duplicando su nivel de producto de y’ a
2y’ requiere duplicar todos los niveles de
insumos
El coste total de producción se duplica
p p

52. Retornos constantes a escala y costes
totales
t t l promediodi
Si la tecnología de una firma exhibe
retornos constantes a escala entonces
duplicando su nivel de producto de y ay’
2y’ requiere duplicar todos los niveles de
insumos
El coste total de producción se duplica
El coste promedio de producción no
cambia

53. Retornos decrecientes a escala y costes
totales
t t l promediodi
Si la tecnología de una firma exhibe
retornos decrecientes a escala
entonces duplicando el nivel de
p
producto de y’ a 2y’ requiere más
y y q
que duplicar todos los insumos

54. Retornos decrecientes a escala y costes
totales
t t l promediodi
Si la tecnología de una firma exhibe
retornos decrecientes a escala
entonces duplicando el nivel de
p
producto de y’ a 2y’ requiere más
y y q
que duplicar todos los insumos
El coste total de producción cuesta
más que el doble

55. Retornos decrecientes a escala y costes
totales
t t l promediodi
Si la tecnología de una firma exhibe
retornos decrecientes a escala
entonces duplicando el nivel de
p
producto de y’ a 2y’ requiere más
y y q
que duplicar todos los insumos
El coste total de producción cuesta
más que el doble
Se incrementa el coste promedio de
p
producción

56. Retornos crecientes a escala y costes
totales
t t l promediodi
Si la tecnología de una firma exhibe
retornos crecientes a escala
entonces duplicando el nivel de
p
producto de y’ a 2y’ requiere menos
y y q
que duplicar todos los insumos

57. Retornos crecientes a escala y costes
totales
t t l promediodi
Si la tecnología de una firma exhibe
retornos crecientes a escala
entonces duplicando el nivel de
p
producto de y’ a 2y’ requiere menos
y y q
que duplicar todos los insumos
El coste total de producción cuesta
menos que el doble

58. Retornos crecientes a escala y costes
totales
t t l promediodi
Si la tecnología de una firma exhibe
retornos crecientes a escala
entonces duplicando el nivel de
p
producto de y’ a 2y’ requiere menos
y y q
que duplicar todos los insumos
El coste total de producción cuesta
menos que el doble
Disminuye el coste promedio de
p
producción

59. Retornos a escala y costes totales
promedio
di
$/unid.
$/unid producto
CTP(y)
CTP( ) r.a.e. decreciente
r.a.e. constante
r.a.e. creciente
y

60. Retornos a escala y costes totales
¿Qué implica esto para las formas de
las funciones de coste total?

61. Retornos a escala y costes totales
Cost. prom. incrementa con y si la
$ tecnología de la firma exhibe r.a.e.
decreciente
c(2y )
c(2y’) Pend. c(2y’)/2y’
Pend = c(2y )/2y
= CTP(2y’).
Pend.
Pend = c(y’)/y’
= CTP(y’).
c(y )
c(y’)
y’ 2y’ y

62. Retornos a escala y costes totales
Cost. prom. incrementa con y si la
$ tecnología de la firma exhibe r.a.e.
decreciente c(y)
c(2y )
c(2y’) Pend. c(2y’)/2y’
Pend = c(2y )/2y
= CTP(2y’).
Pend.
Pend = c(y’)/y’
= CTP(y’).
c(y )
c(y’)
y’ 2y’ y

63. Retornos a escala y costes totales
Cost. prom. disminuye con y si la
$ tecnología de la firma exhibe r.a.e.
creciente
c(2y’)
Pend. c(2y’)/2y’
Pend = c(2y )/2y
c(y’) = CTP(2y’).
Pend.
Pend = c(y’)/y’
= CTP(y’).
y’ 2y’ y

64. Retornos a escala y costes totales
Cost. prom. disminuye con y si la
$ tecnología de la firma exhibe r.a.e.
creciente c(y)
c(2y’)
Pend. c(2y’)/2y’
Pend = c(2y )/2y
c(y’) = CTP(2y’).
Pend.
Pend = c(y’)/y’
= CTP(y’).
y’ 2y’ y

65. Retornos a escala y costes totales
Cost. prom. es constante cuando la
$ tecnología de las firmas exhibe r.a.e.
c(2y’) constante c(y)
=2c(y’)
(y ) Pend. c(2y’)/2y’
Pend = c(2y )/2y
= 2c(y’)/2y’
= c(y’)/y’
c(y )/y
c(y’)
por lo que,
CTP(y ) CTP(2y’)
CTP(y’) = CTP(2y ).
y’ 2y’ y

66. Costes totales de corto y largo p
g plazo
En el largo plazo una firma puede
variar el nivel de todos sus insumos
Consideremos una firma que no
puede cambiar el nivel del insumo 2
de x2’ unidades
¿Cómo se comparan las curvas de
Có l d
costes totales de corto y largo plazo
de producir y unidades de producto?

67. Costes totales de corto y largo p
g plazo
El problema de minimización de
costes de largo plazo es
min w 1 x1 + w 2 x 2
i
x1 , x 2 ≥ 0
sujeto a
j t f ( x1 , x 2 ) = y .
El problema de minimización de
costes de corto plazo es
′
min w 1 x1 + w 2 x 2
x1 ≥ 0
sujeto a ′
f ( x1 , x 2 ) = y .

68. Costes totales de corto y largo p
g plazo
El problema de min. de coste de corto
p
plazo es el problema de largo plazo
sujeto a la restricción extra x2 = x2’
Si la elección de largo plazo para x2
fuera x2’ entonces la restricción extra
x2 = x2’ no es en realidad una
restricción y por ello los costes de
corto y largo plazo de producir y
unidades de producto son los mismos

69. Costes totales de corto y largo p
g plazo
El problema de min. de costes de corto
p
plazo es por lo tanto el problema de
largo plazo sujeto a la restricción extra
x2 = x2”
Pero, si la elección de largo plazo para
x2 ≠ x2” entonces la restricción extra x2
= x2” evita que la firma logre en el
corto plazo su coste total de
producción de largo plazo de producir
y unidades de producto

70. Costes totales de corto y largo p
g plazo
y ′′′
x2 Consideremos 3 niveles de
y ′′ producto
y′
x1

71. Costes totales de corto y largo p
g plazo
y ′′′ En el largo plazo cuando la
x2
firma es libre de elegir tanto
y ′′
x1 como x2, la cesta de
insumos menos costosa
y′
es ...
x1

72. Costes totales de corto y largo p
g plazo
y ′′′ senda de
x2 expansión
y ′′ del
producto de
y′ largo plazo
x 2′′
′
x 2′
′
x2 ′
x1 x1′ x1′′
′ ′ ′ x1

73. Costes totales de corto y largo p
g plazo
y ′′′ senda de Costes de largo
x2 expansión plazo son:
y ′′ del c ( y ′) = w1 x1 + w2 x2
′ ′
producto de c ( y ′′) = w1 x1′ + w2 x2′′
′ ′
y′ largo plazo
c ( y ′′′) = w1 x1′′+ w2 x2′′
′ ′
x 2′′
′
x 2′
′
x2 ′
x1 x1′ x1′′
′ ′ ′ x1

74. Costes totales de corto y largo p
g plazo
Ahora supongamos que la firma
tiene la restricción de corto plazo
x2 = x2”

75. Costes totales de corto y largo p
g plazo
y ′′′ senda de Costes de largo
x2 plazo son:
expansión
ió
y ′′ del producto c ( y ′) = w1 x1 + w 2 x 2
′ ′
d corto plazo c ( y ′′) = w1 x1′ + w 2 x 2′′
de t l ′ ′
y′ c ( y ′′′) = w1 x1′′+ w 2 x 2′′
′ ′
x 2′′
′
x 2′
′
x2 ′
x1 x1′ x1′′
′ ′ ′ x1

76. Costes totales de corto y largo p
g plazo
y ′′′ senda de Costes de largo
x2 plazo son:
expansión
ió
y ′′ del producto c ( y ′ ) = w 1 x 1′ + w 2 x 2 ′
de
d corto plazo
t l c ( y ′′ ) = w 1 x 1′′ + w 2 x 2′′
′
y′ c ( y ′′′ ) = w 1 x 1′′′+ w 2 x 2′′
′
x 2′′
′
x 2′
′
x2 ′
x1 x1′ x1′′
′ ′ ′ x1

77. Costes totales de corto y largo p
g plazo
y ′′′ senda de Costes de largo
x2 plazo son:
expansión
ió c ( y ′ ) = w 1 x 1′ + w 2 x 2
′
y ′′ del producto c ( y ′′ ) = w x ′′ + w x ′′′
1 1 2 2
de
d corto plazo c ( y ′′′ ) = w x ′′′+ w x ′′′
t l
′
1 1 2 2
y
Costes de corto plazo
x 2′′
′ son:
x 2′
′ c s ( y ′) > c ( y ′)
x2 ′
x1 x1′ x1′′
′ ′ ′ x1

78. Costes totales de corto y largo p
g plazo
Costes de largo
y ′′′ senda de
x2 plazo son:
expansión
ió c ( y ′ ) = w 1 x1 + w 2 x 2
′ ′
y ′′ del producto
c ( y ′′ ) = w 1 x 1′ + w 2 x 2′′
′ ′
de
d corto plazo
t l
c ( y ′′′ ) = w 1 x 1′′+ w 2 x 2′′
′ ′
y′
Costes de corto plazo
x 2′′
′ son:
x 2′
′ c s ( y ′) > c ( y ′)
x2 ′ c s ( y ′′ ) = c ( y ′′ )
x1 x1′ x1′′
′ ′ ′ x1

79. Costes totales de corto y largo p
g plazo
Costes de largo
y ′′′ senda de
x2 plazo son:
expansión
ió ′ ′ ′
y ′′ del producto c ( y ) = w 1 x1 + w 2 x 2
c ( y ′′ ) = w 1 x1′ + w 2 x 2′′
′ ′
de
d corto plazo
t l
′ c ( y ′′′ ) = w 1 x1′′+ w 2 x 2′′
′ ′
y
Costes de corto plazo
x 2′′
′ son:
x 2′
′ c s ( y ′) > c ( y ′)
x2 ′ c s ( y ′′ ) = c ( y ′′ )
x1 x1′ x1′′
′ ′ ′ x1

80. Costes totales de corto y largo p
g plazo
Costes de largo
y ′′′ senda de
plazo son:
p
x2 expansión
ió c ( y ′ ) = w 1 x1 + w 2 x 2
′ ′
y ′′ del producto c ( y ′′ ) = w x ′′ + w x ′′′
1 1 2 2
de
d corto plazo c ( y ′′′ ) = w x ′′′+ w x ′′′
t l
′
1 1 2 2
y Costes de corto plazo
x 2′′
′ son:
c s ( y ′) > c ( y ′)
x 2′
′ c s ( y ′′ ) = c ( y ′′ )
x2 ′
c s ( y ′′′ ) > c ( y ′′′ )
x1 x1′ x1′′
′ ′ ′ x1

81. Costes totales de corto y largo p
g plazo
Coste total de corto plazo es
superior al coste total de largo plazo
excepto para el nivel de producto
donde la restricción del nivel de
insumo de corto plazo es la elección
del nivel de insumo de largo plazo
Esto significa que la curva de coste
tota
total de largo plazo siempre t e e u
a go p a o s e p e tiene un
punto en común con cualquier curva
de coste total de corto plazo

82. Costes totales de corto y largo p
g plazo
$ En el corto plazo la curva de coste total
siempre tiene un punto en común con
con la curva de coste total de largo plazo,
y es en cualquier otro punto es superior a
la curva de coste total de largo plazo
cs(y)
c(y)
F =
w 2 x 2′
′
y′ y ′′ y ′′′
y