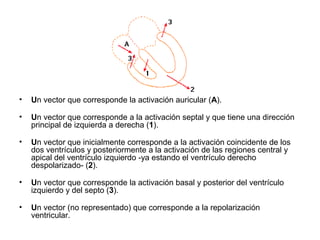
Los vectores se pueden usar para representar la actividad eléctrica del corazón durante la despolarización y repolarización. La despolarización se representa con un vector cuya cabeza es positiva y cola negativa, mientras que la repolarización es lo opuesto, con la cabeza del vector siendo negativa y la cola positiva. La orientación del vector respecto a los electrodos determina si la señal en el ECG es positiva o negativa.

1. Vectores
• Un vector es un ente matemático que
posee dirección sentido y magnitud.
• La dirección se refiere a la posición del
vector: Horizontal, vertical, oblicuo, etc.
• El sentido señala la orientación: De arriba
hacia abajo, de Norte a Sur etc.
• La magnitud es tamaño del vector, es el
valor numérico del mismo.

2. Representación gráfica de vectores

3. • Gráficamente: Un vector se representa como un
segmento orientado, identificando sus extremos
mediante dos letras mayúsculas, o colocado una sola
letra minúscula en al segmento.

4. Suma gráfica de vectores

5. Con más de dos vectores

6. Componentes de un vector
• Podemos definir la posición de un vector en el plano mediante sus
componentes referidas a unos ejes de coordenadas.
• Para hallar las componentes de un vector basta ver cuantas
unidades avanza horizontal y verticalmente desde su origen hasta
su extremo. Para ello hallamos la diferencia entre las coordenadas
del punto extremo y el punto origen del vector.

7. Escrito matemáticamente
• Sea α el ángulo que
forma con el eje
horizontal
• Sea axy ay las
proyecciones en los ejes
x e y respectivamente

8. Usando trigonometría, recordemos:
Hipotenusa
opuestocat
sen
.
=α
Cat. Opuesto
al ángulo
Cat. adyacente
al ángulo
Hipotenusa
adyacentecat.
cos =α
α
α
α
cos
tan
sen
=

9. Luego:
a
a
sen
y
=α
a
ax
=αcos
x
y
a
asen
==
α
α
α
cos
tan

10. Sea por lo tanto cada componente escrita de la siguiente
forma

11. Donde:
a

Representa el módulo del vector “a”
kji ˆ;ˆ;ˆ Representan vectores unitarios
para los ejes x,y,z respectivamente

12. Operaciones con vectores
• Suma de vectores:
• Un vector que posee diferentes
componentes se sumara a otro
respetando estas componentes, es decir
se sumaran los términos que
correspondan al mismo grupo de pares
ordenados.

13. Sumando dos vectores y sus proyecciones

14. Producto punto
• El producto o multiplicación de vectores
se puede realizar de la misma forma en
que se resuelven los polinomios, pero
respetando un par de reglas para los
vectores unitarios.

15. 1ˆˆˆˆˆˆ =⋅=⋅=⋅ kkjjii
0ˆˆˆˆ
0ˆˆˆˆ
0ˆˆˆˆ
=⋅=⋅
=⋅=⋅
=⋅=⋅
ikki
jkkj
ijji

16. Ejemplo:
• Sean los siguientes
vectores:
kbjbibB
kajaiaA
zyx
zyx
ˆˆˆ
ˆˆˆ
++=
++=


BAC

⋅=

17. )ˆˆˆ()ˆˆˆ( kbjbibkajaiaC zyxzyx ++⋅++=
)ˆˆ()ˆˆ()ˆˆ(
)ˆˆ()ˆˆ()ˆˆ(
)ˆˆ()ˆˆ()ˆˆ(
kkbajkbaikba
kjbajjbaijba
kibajibaiibaC
zzyzxz
zyyyxy
zxyxxx
⋅⋅⋅+⋅⋅⋅+⋅⋅⋅
+⋅⋅⋅+⋅⋅⋅+⋅⋅⋅+
+⋅⋅⋅+⋅⋅⋅+⋅⋅⋅=
0 0
00
0 0

18. )ˆˆ()ˆˆ()ˆˆ( kkbajjbaiibaC zzyyxx ⋅⋅⋅+⋅⋅⋅+⋅⋅⋅=
1 1 1
zzyyxx bababaC ⋅+⋅+⋅=
El resultado es un escalar (NO VECTOR)

19. Módulo de un vector
AAA

⋅=
Matemáticamente se escribe:
si
kajaiaA yyx
ˆˆˆ ++=

El modulo representa el tamaño del vector
Y es un escalar.

20. 222
zyx aaaA ++=

Además se define el vector unitario del
vector A
A
A
A 

=ˆ

21. Producto Cruz
• El producto cruz (X) es otro tipo de
producto entre vectores, a diferencia del
producto usual o punto su resultado es un
vector.
• Al igual que en el caso anterior existen
reglas que se deben respetar.

22. 0ˆˆˆˆˆˆ =×=×=× kkjjii
jik
jki
ijk
ikj
kij
kji
ˆˆˆ
ˆˆ
ˆˆˆ
ˆˆˆ
ˆˆˆ
ˆˆˆ
=×
−=×
−=×
=×
−=×
=×
No es conmutativo

23. Existe una regla mnemotécnica para el producto cruz
iˆ
jˆ
kˆ
X
=
( + )
Producto en sentido Horario
es positivo

24. iˆ
jˆ
kˆ
X
=
( - )
Producto en sentido anti-
horario es negativo

25. Ejemplo:
• Sean nuevamente los
siguientes vectores:
kbjbibB
kajaiaA
zyx
zyx
ˆˆˆ
ˆˆˆ
++=
++=


BAC

×=

26. )ˆˆˆ()ˆˆˆ( kbjbibkajaiaC zyxzyx ++×++=

)ˆˆ()ˆˆ()ˆˆ(
)ˆˆ()ˆˆ()ˆˆ(
)ˆˆ()ˆˆ()ˆˆ(
kkbajkbaikba
kjbajjbaijba
kibajibaiibaC
zzyzxz
zyyyxy
zxyxxx
×⋅⋅+×⋅⋅+×⋅⋅
+×⋅⋅+×⋅⋅+×⋅⋅+
+×⋅⋅+×⋅⋅+×⋅⋅=
 0
0
0

27. )ˆˆ()ˆˆ(
)ˆˆ()ˆˆ(
)ˆˆ()ˆˆ(
jkbaikba
kjbaijba
kibajibaC
yzxz
zyxy
zxyx
×⋅⋅+×⋅⋅
+×⋅⋅+×⋅⋅+
+×⋅⋅+×⋅⋅=

iˆ
jˆ
kˆ jˆ−
kˆ−
iˆ−

28. )ˆ()ˆ()ˆ(
)ˆ()ˆ()ˆ(
ibajbaiba
kbajbakbaC
yzxzzy
xyzxyx
−⋅⋅+⋅⋅+⋅⋅+
+−⋅⋅+−⋅⋅+⋅⋅=

)ˆ()(
)ˆ()()ˆ()(
jbaba
ibabakbabaC
zxxz
yzzyxyyx
⋅⋅−⋅+
+⋅⋅−⋅+⋅⋅−⋅=

)ˆ()(
)ˆ()()ˆ()(
kbaba
jbabaibabaC
xyyx
zxxzyzzy
⋅⋅−⋅+
+⋅⋅−⋅+⋅⋅−⋅+=
 Reordenando

29. Ejemplo numérico
kjiB
kjiA
ˆ4ˆ2ˆ1
ˆ3ˆ1ˆ2
++=
++=


BAC

×=

30. )ˆˆ(6)ˆˆ(3
)ˆˆ(4)ˆˆ(1)ˆˆ(8)ˆˆ(4
)ˆ4ˆ2ˆ1()ˆ3ˆ1ˆ2(
jkik
kjijkijiC
kjikjiBAC
×+×+
+×+×+×+×=
++×++=×=


)ˆ(6ˆ3ˆ4)ˆ(1)ˆ(8ˆ4 ijikjkC −+++−+−+=

iC ˆ2−=

jˆ5− kˆ3+

31. Una aplicación simple de vectores
• El ciclo cardíaco puede representarse de forma simple con los
siguientes vectores que aparecen de forma sucesiva en el tiempo:

32. VECTORES ELÉCTRICOS
El potencial que registra un electrodo depende de la variación
en el tamaño, la geometría y la posición que ocupa
sucesivamente la superficie que separa el área activa de la de
reposo durante la despolarización y la repolarización. Durante
la despolarización el área activa será negativa con respecto a
la que aún está en reposo, es decir, que la excitación se
propaga como un frente que lleva cargas positivas en la
”cabeza” y deja cargas negativas en la ”cola”. Estos dipolos
pueden representarse mediante vectores que se dirigen hacia
la parte positiva y cuya magnitud depende de la superficie libre
del órgano que está despolarizada. Si este vector se proyecta
sobre una línea de derivación el tamaño y polaridad de esta
proyección corresponde a la amplitud y la polaridad de la onda
que se registra en ese momento.

33. Para la proyección de los vectores en el plano, se
supone que los miembros forman los vértices de
un triángulo equilátero (Triángulo de Einthoven)
cuyo centro es ocupado por el corazón y cuyos
lados constituyen las líneas de derivación Dl, Dll
y Dlll. Se supone también que el cuerpo se
comporta como un conductor homogéneo.

34. . Proyecciones de un vector (flecha sombreada) sobre el triángulo de
Einthoven y el sistema triaxial

36. • Un vector que corresponde la activación auricular (A).
• Un vector que corresponde a la activación septal y que tiene una dirección
principal de izquierda a derecha (1).
• Un vector que inicialmente corresponde a la activación coincidente de los
dos ventrículos y posteriormente a la activación de las regiones central y
apical del ventrículo izquierdo -ya estando el ventrículo derecho
despolarizado- (2).
• Un vector que corresponde la activación basal y posterior del ventrículo
izquierdo y del septo (3).
• Un vector (no representado) que corresponde a la repolarización
ventricular.

37. • En pocas palabras.
• La despolarización o activación y la
repolarización o activación de los
miocitos, se representa con un vector con
diferentes cargas en su cabeza (punta del
vector) y en su cola (origen del vector).
• La despolarización: se representa con un
vector cuya cabeza es positiva y cola
negativa.

38. • La orientación angular o derivación de
todo electrodo del vector, lo que define el
carácter positivo o negativo del mismo da
origen al ECG.
• En la repolarización el vector será
negativo en la cabeza del mismo y
positivo en la cola.

39. Por lo dicho anteriormente, cada una de estas
zonas tiene su correspondencia en el ECG