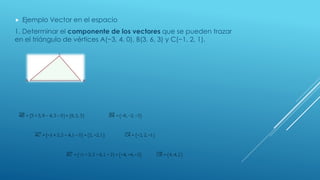
Este documento presenta conceptos básicos sobre vectores en el plano y en el espacio. Define un vector como un segmento orientado con magnitud, dirección y sentido. Explica que un vector en el plano se caracteriza por su dirección, origen, punto de aplicación y longitud. Incluye ejemplos de vectores en el plano y en el espacio. También define los componentes de un vector como magnitud, dirección y sentido.

1. BACHILLER:
GARCIA CARRASQUEL
JUAN CARLOS
C:I: 26.632.536

2. EJEMPLO DE PLANO Y 2 EJEMPLOS DE
ESPACIO
Temas en desarrollo:
 Vectores en el Plano
 Ventores en el espacio (Definición Y Características)
 Magnitud
 Dirección
 Sentido

3.  Vectores en el Plano
Un vector es un segmento orientado que tiene una dirección
determinada, un sentido y un módulo.
Los vectores han sido utilizados en diversos ámbitos de la ciencia
no tan solo en matemáticas.
 Un vector en el plano se Caracteriza por :
 a) Su dirección
 b) Su origen o sentido
 c) Su punto de aplicación
 d) Su longitud o módulo

4.  Ejemplo Vector plano
1. Dado el vector U = (2, - 1), determinar dos vectores equivalentes a U , AB y
CD , sabiendo que A(1, -3) y D(2, 0). Para que los vectores sean
equivalentes debe cumplirse:
U = AB
(2, -1 ( XB - 1, YB + 3)
2 = XB - 1 XB = -3
AB = 3, -4
-1 = YB + 3 YB = -4
Independientemente, para obtener otro vector equivalente:
U = CD
(2, -1 = (2 –XC, 0-YC)
2=2- XC XC= 0
(CD = 0,1)
-1 =YC YC= 1

5.  Vector en el espacio:
Un vector en el espacio es cualquier segmento orientado que tiene
su origen en un punto y su extremo en el otro.
 Características:
Es el punto exacto sobre el que actúa el vector.
Módulo: Es la longitud o tamaño del vector. Para hallarla es
preciso conocer el origen y el extremo del vector,
Para saber cuál es el módulo del vector, debemos medir desde su
origen hasta su extremo.

6.  Ejemplo Vector en el espacio
1. Determinar el componente de los vectores que se pueden trazar
en el triángulo de vértices A(−3, 4, 0), B(3, 6, 3) y C(−1, 2, 1).

7.  Ejemplo 2.
Dados los vectores y , hallar los módulos de y

8.  Magnitud:
La magnitud es una propiedad que poseen los Fenómenos o las
relaciones entre ellos
Permite que puedan ser medidos (expresados por números reales
no negativos y usando la unidad pertinente).
Dicha medida, es representada por una Cantidad.
Una magnitud es el resultado de una medición;
Magnitudes matemáticas tienen definiciones abstractas, mientras
que las magnitudes físicas se miden con instrumentos apropiados.

9.  Dirección:
Es la dirección de la recta que lo contiene. Si dos vectores tienen la
misma recta o son paralelos tienen la misma dirección.
depende del Sistema de Referencia en el que se describa el
movimiento; es decir el punto de vista del observador.

10.  Sentido:
El sentido es uno de los componentes de un vector, deben ser
definidas por su modulo y dirección en las matemáticas. En física,
la especificación de un vector todavía necesita una cuarta
especificación, la unidad de medición.
la dirección y sentido se representan como flechas, y la dirección
es indicada por el Angulo entre la flecha y el plano de referencia y
la dirección indicada por el extremo de la flecha.