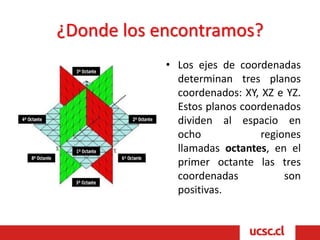
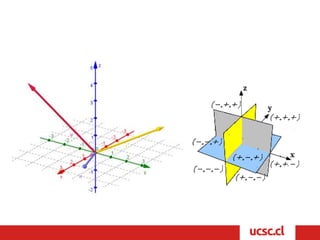
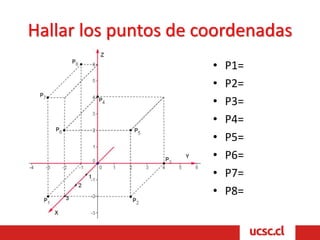
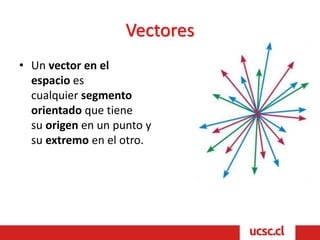
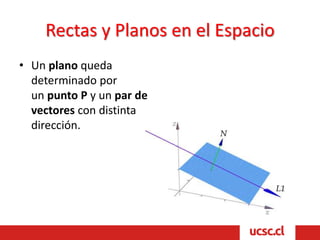
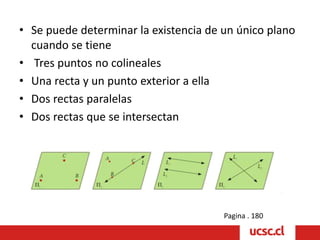
Este documento describe conceptos básicos de vectores y geometría en el espacio tridimensional. Explica que un sistema de coordenadas tridimensional se construye trazando ejes perpendiculares X, Y y Z, y que cada punto en el espacio se define por tres coordenadas. También describe cómo los ejes dividen el espacio en ocho regiones llamadas octantes, y define vectores como segmentos orientados con origen y extremo, cuyas componentes son las coordenadas del extremo menos las del origen. Finalmente, introduce conceptos básicos de planos

1. Vectores en el Espacio
Profesor: Luciano Rojas C.
4to medio

2. ¿Donde los encontramos?
• Un sistema de
coordenadas
tridimensional se
construye trazando un eje
Z, perpendicular en el
origen de coordenadas a
los ejes X e Y.
• Donde cada punto viene
determinado por tres
coordenadas P(x, y, z).

3. ¿Donde los encontramos?
• Los ejes de coordenadas
determinan tres planos
coordenados: XY, XZ e YZ.
Estos planos coordenados
dividen al espacio en
ocho regiones
llamadas octantes, en el
primer octante las tres
coordenadas son
positivas.

6. Hallar los puntos de coordenadas
• P1=
• P2=
• P3=
• P4=
• P5=
• P6=
• P7=
• P8=

7. Vectores
• Un vector en el
espacio es
cualquier segmento
orientado que tiene
su origen en un punto y
su extremo en el otro.

8. Vectores
Componentes
• Si las coordenadas de A y B son:
A(x1, y1, z1) y B(x2, y2, z2)
Las coordenadas o componentes
del vector son las coordenadas
del extremo menos las
coordenadas del origen.
• 𝐴𝐵 = 𝑥2 − 𝑥1, 𝑦2 − 𝑦1 , 𝑧2 −

9. Modulo del vector
Cálculo del módulo conociendo
sus componentes
• El módulo de un vector es
la longitud del segmento ori
entado que lo define.
• El módulo de un vector es
un número siempre positiv
o y solamente el vector
nulo tiene módulo cero.
• 𝑢 = 𝑥2
+ 𝑦2
+ 𝑧2

10. ¿En que octante se encuentran?
Dibuje
• 𝑢 = 1,1,1
• 𝑏 = −4,5,6
• 𝑎 = 2, −6,2
• 𝑡 = 0,0, −1
• 𝑤 = −5 , −12,6
• 𝑣 = 8, −3, −7
• 𝑝 = −1, −1, −1
• 𝑞 = 1, −1,1
• 𝑙 = 5,3, −1

11. Rectas y Planos en el Espacio
• Un plano queda
determinado por
un punto P y un par de
vectores con distinta
dirección.

12. • Se puede determinar la existencia de un único plano
cuando se tiene
• Tres puntos no colineales
• Una recta y un punto exterior a ella
• Dos rectas paralelas
• Dos rectas que se intersectan
Pagina . 180

13. • Dos planos en el espacio pueden ser paralelos,
coincidentes o secantes.
• Paralelos: NO tienen punto de intersección.
• Secantes: Cuando su intersección determina una
recta y, por ende, posee infinitos puntos de
intersección: todos los puntos que pertenecen a esa
recta.
• Coincidentes: Cuando tienen todos sus puntos en
Común

14. Observación ¿Qué sucede si…?
• ¿Que sucede si dos
rectas en el espacio no
son paralelas, ni
secantes?.
• Esto quiere decir que
son rectas alabeadas y
no se puede definir en
el plano que las
contenga.