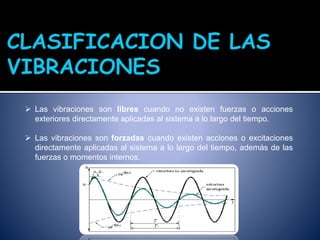
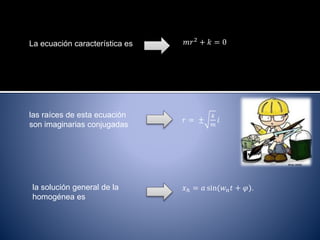
El documento describe las vibraciones mecánicas. Explica que las vibraciones son oscilaciones alternativas alrededor de una posición de equilibrio. Las vibraciones pueden ser libres o forzadas dependiendo de si hay una fuerza externa aplicada. También cubre la clasificación de las vibraciones, la ecuación diferencial que las describe, y el fenómeno de resonancia que ocurre cuando la frecuencia forzada es igual a la frecuencia natural del sistema.

1. VIBRACIONES
MECANICAS

2.  Se dice que un cuerpo vibra cuando experimenta
cambios alternativos, de tal modo que sus puntos
oscilen sincrónicamente en torno a sus posiciones
de equilibrio, sin que el campo cambie de lugar.

3. Este intercambio de energía puede ser
producido por:
 Como otro concepto
de vibración, se
puede decir que es
un intercambio de
energía cinética en
cuerpos con rigidez
y masas finitas, el
cual surge de una
entrada de energía
dependiente del
tiempo.
Desequilibrio
en máquinas
rotatorias
Entrada de
Energía
Acústica
*
Circulación de
Fluidos o masas
Energía
Electromagnética
*

4. 𝑚𝑥´´ + 𝑐𝑥´ + 𝑘𝑥 = 𝑓(𝑡)

5. Cualquier sistema de un solo grado de libertad puede describirse por
medio de la misma forma de ecuación diferencial escrita anteriormente, si
la fuerza del resorte es proporcional al desplazamiento y la fuerza de
rozamiento es proporcional a la velocidad. Para el sistema general de un
solo grado de libertad podemos escribir:
𝑚 𝑒 𝑥´´ + 𝑐 𝑒 𝑥´ + 𝑘 𝑒 𝑥 = 𝑓(𝑡)
 Donde me ,ce, ke son la masa equivalente, la constante de
amortiguamiento equivalente y la constante del resorte
equivalente, respectivamente. El desplazamiento X puede ser
lineal o angular.

6.  Las vibraciones son libres cuando no existen fuerzas o acciones
exteriores directamente aplicadas al sistema a lo largo del tiempo.
 Las vibraciones son forzadas cuando existen acciones o excitaciones
directamente aplicadas al sistema a lo largo del tiempo, además de las
fuerzas o momentos internos.

7. Las vibraciones mecánicas pueden clasificarse desde
diferentes puntos de vistas dependiendo de: a) la
excitación, b) la disipación de energía, c) la linealidad
de los elementos y d) de las características de la señal.

8.  Una Vibración libre es cuando un sistema vibra debido a una
excitación del tipo instantánea, mientras que la vibración forzada se
debe a una excitación del tipo permanente.
 Esta importante clasificación nos dice que un sistema vibra
libremente si solo existen condiciones iniciales del movimiento, ya sea
que suministremos la energía por medio de un impulso (energía
cinética) o debido a que posee energía potencial, por ejemplo
deformación inicial de un resorte.

9.  El amortiguamiento es un sinónimo de la perdida de energía de sistemas
vibratorios y se manifiesta con la disminución del desplazamiento de vibración.
Este hecho puede aparecer como parte del comportamiento interno de un
material por ejemplo la fricción, o bien, o como un elemento físico llamado
precisamente amortiguador.
 Por lo tanto, la vibración amortiguada es aquella en la que la frecuencia de
oscilación de un sistema se ve afectada por la disipación de la energía, pero
cuando la disipación de energía no afecta considerablemente a la frecuencia
de oscilación entonces la vibración es del tipo no amortiguada.

10.  Si el comportamiento de cada uno de los parámetros de los componentes
básicos de un sistema es del tipo lineal la vibración resultante es lineal, en
caso contrario será del tipo no lineal. En la realidad todo elemento se
comporta como un elemento no lineal pero si bajo ciertas condiciones se
puede considerar como un elemento lineal, entonces el análisis se facilita
considerablemente.
 Por ejemplo, un resorte helicoidal en donde según la ley de Hooke el
comportamiento fuerza-deformación es lineal aunque en la realidad los
resortes helicoidales tienen un comportamiento no lineal pero este que puede
ser aproximado a un elemento lineal y facilitar su estudio sin afectar
considerablemente el comportamiento real.

11. VIBRACIONES
FORZADAS NO
AMORTIGUADAS

12.  Para mantener un sistema oscilando es necesario suministrar energía al
sistema, cuando esto se lleva a cabo se dice que la vibración es
forzada.
 Si se introduce energía en el sistema a un ritmo mayor del que se
disipa, la energía aumenta con el tiempo, lo que se manifiesta por un
aumento de la amplitud del movimiento. Si la energía se proporciona al
mismo ritmo que se disipa, la amplitud permanece constante con el
tiempo.
La ecuación diferencial del
movimiento, teniendo en cuenta
que la fuerza es de tipo periódico,
es:
𝑚𝑥′′
+ 𝑘𝑥 = 𝐹 = 𝐹0 cos 𝜔𝑡

13. La ecuación característica es 𝑚𝑟2 + 𝑘 = 0
las raíces de esta ecuación
son imaginarias conjugadas
𝑟 = ±
𝑘
𝑚
𝑖
la solución general de la
homogénea es
𝑥ℎ = 𝑎 sin(𝑤 𝑛 𝑡 + 𝜑).

14. La solución particular de la completa es 𝑥 𝑝 = 𝐴 cos 𝑤𝑡 .
Así, la solución general tiene por expresión:
𝑥 = 𝑎 cos(𝑤 𝑛 𝑡 + 𝜑) +
𝐹𝑜
𝑘
1 −
𝑤2
𝑤 𝑛
2

15.  En todo sistema no amortiguado y forzado armónicamente, el
movimiento resultante se compone de la suma de dos armónicos, uno
de frecuencia natural 𝑤 𝑛 y otro de frecuencia de la fuerza exterior 𝑤.
 La amplitud del primero depende de las condiciones iniciales y se
anula para unos valores particulares, la amplitud del segundo depende
de la proximidad de ambas frecuencias a través de la expresión
denominada factor de resonancia:
𝜌 =
1
1 −
𝑤2
𝑤0
2
=
𝐴
𝑥 𝑐𝑠𝑡

16.  Fenómeno producido cuando la frecuencia natural del
sistema 𝑤 𝑛 toma un valor muy próximo a la frecuencia de la
fuerza exterior 𝜔, es decir, en el caso particular en que 𝑤 𝑛 =
𝜔 + ∆𝜔 . Para perturbación inicial nula 𝑥 𝑜 = 𝑥′ 𝑜 = 0 se
obtiene:
𝑥 =
𝐹𝑜 𝑤0
𝑘∆𝜔
sin
∆𝜔
2
𝑡 sin 𝑤0 𝑡

17.  Una característica muy significativa del movimiento oscilatorio tiene lugar
cuando la fuerza excitadora de las vibraciones tiene unas frecuencias
particulares, para cada sistema dado, produciéndose cambios de
configuración de los sistemas mecánicos que alcanzan amplitudes
notables, y generalmente, ocasionan un fallo estructural del material
sometido a esfuerzos de rotura: efectos resonantes.
 Este riesgo se produce incluso con fuerzas excitadoras muy pequeñas ya
que depende de las características del material sometido a vibración.

18.  Cuando la frecuencia de la fuerza exterior es igual a la frecuencia
natural del sistema 𝜔 = 𝜔 𝑛 , es decir, cuando ∆𝜔 → 0, se produce la
resonancia, la ecuación que rige dicho fenómeno es:
𝑥 =
𝐹0 𝜔
2𝑘
𝑡 sin 𝜔 𝑛 𝑡
 Expresión que corresponde a un movimiento armónico de frecuencia
𝑤 𝑛 y cuya amplitud tiende a infinito cuando 𝑡 → ∞.

19. GRACIAS