Un resumen sobre los primeros geómetras

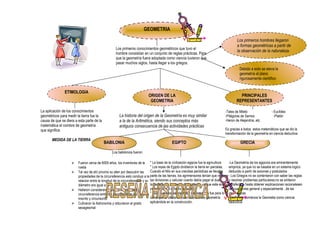
1. GEOMETRIA
Los primeros conocimientos geométricos que tuvo el
hombre consistían en un conjunto de reglas prácticas. Para
que la geometría fuera adoptada como ciencia tuvieron que
pasar muchos siglos, hasta llegar a los griegos.
Debido a esto se eleva la
geometría al plano
rigurosamente científico
ETIMOLOGIA
La aplicación de los conocimientos
geométricos para medir la tierra fue la
causa de que se diera a esta parte de la
matemática el nombre de geometría
que significa:
MEDIDA DE LA TIERRA
ORIGEN DE LA
GEOMETRIA
La historia del origen de la Geometría es muy similar
a la de la Aritmética, siendo sus conceptos más
antiguos consecuencia de las actividades prácticas
Los primeros hombres llegaron
a formas geométricas a partir de
la observación de la naturaleza.
PRINCIPALES
REPRESENTANTES
BABILONIA EGIPTO GRECIA
 Fueron cerca de 6000 años, los inventores de la
rueda
 Tal vez de ahí provino su afan por descubrir las
propiedades de la circunsferencia esto condujo a la
relacion entre la longitud de la circunsferencia y su
diámetro era igual a 3
 Hallaron considerando que la longitud de la
circunsferencia entre los perímetros de los cuadros
inscrito y circunscrito
 Cultvaron la Astronomia y obtuvieron el grado
sexagesimal
Los babilonios fueron:
* La base de la civilización egipcia fue la agricultura
* Los reyes de Egipto dividieron la tierra en parcelas.
Cuando el Nilo en sus crecidas periódicas se llevaba
parte de las tierras, los agrimensores tenían que rehacer
las divisiones y calcular cuanto debía pagar el dueño de
la parcela por concepto de impuesto ya que este era
proporcional a la tierra cultivada
* Para la necesidad de medir las tierras no fue para lo
único que la utilizaron pues cultivaron la geometría
aplicándola en la construcción.
-La Geometría de los egipcios era eminentemente
empirica, ya que no se basaba en un sistema logico
deducido a partir de axiomas y postulados
- Los Griegos no se contentaron con saber las reglas
y resolver problemas particulares;no se sintieron
satisfechos hasta obtener explicaciones racionalesen
las cuestiones general y especialmente , de las
geometricas
-En Grecia comienza la Geometia como ciencia
deductiva.
-Tales de Mileto - Euclides
-Pitágoras de Samos -Platón
-Heron de Alejandria, etc.
Es gracias a todos estos matemáticos que se dio la
transformación de la geometría en ciencia deductiva

2. La historia del origen de la Geometría es muy similar a la de la Aritmética, siendo sus conceptos más antiguos consecuencia de las actividades prácticas. Los primeros hombres llegaron a
formas geométricas a partir de la observación de la naturaleza.
El sabio griego Eudemo de Rodas, atribuyó a los egipcios el descubrimiento de la geometría, ya que, según él, necesitaban medir constantemente sus tierras debido a que las
inundaciones del Nilo borraban continuamente sus fronteras. Recordemos que, precisamente, la palabra geometría significa medida de tierras.
En los matemáticos de la cultura helénica los problemas prácticos relacionados con las necesidades de cálculos aritméticos, mediciones y construcciones geométricas continuaron
jugando un gran papel. Sin embargo, lo novedoso era, que estos problemas poco a poco se desprendieron en una rama independiente de las matemáticas que obtuvo la denominación de
"logística". A la logística fueron atribuidas: las operaciones con números enteros, la extracción numérica de raíces, el cálculo con la ayuda de dispositivos auxiliares, cálculo con fracciones,
resolución numérica de problemas que conducen a ecuaciones de 1er
y 2º grado, problemas prácticos de cálculo y constructivos de la arquitectura, geometría, agrimensura, etc... Al mismo
tiempo ya en la escuela de Pitágoras se advierte un proceso de recopilación de hechos matemáticos abstractos y la unión de ellos en sistemas teóricos. Junto a la demostración
geométrica del teorema de Pitágoras fue encontrado el método de hallazgo de la serie ilimitada de las ternas de números "pitagóricos", esto es, ternas de números que satisfacen la
ecuación a2
+b2
=c2
.
En este tiempo transcurrieron la abstracción y sistematización de las informaciones geométricas. En los trabajos geométricos se introdujeron y perfeccionaron los métodos de
demostración geométrica. Se consideraron, en particular: el teorema de Pitágoras, los problemas sobre la cuadratura del círculo, la trisección de un ángulo, la duplicación del cubo, la
cuadratura de una serie de áreas (en particular las acotadas por líneas curvas). Paralelamente, al ampliarse el número de magnitudes medibles, debido a la aparición de los números
irracionales, se originó una reformulación de la geometría, dando lugar al álgebra geométrica. Esta nueva rama incluía entre otros conceptos el método de anexión de áreas, el conjunto de
proposiciones geométricas que interpretaban las cantidades algebraicas, división áurea, expresión de la arista de un poliedro regular a través del diámetro de la circunferencia circunscrita.
Sin embargo, el álgebra geométrica estaba limitada a objetos de dimensión no mayor que dos, siendo inaccesibles los problemas que conducían a ecuaciones de tercer grado o
superiores, es decir, se hacían imposibles los problemas que no admitieran solución mediante regla y compás. La historia sobre la resolución de los tres problemas geométricos clásicos
(sobre la cuadratura del círculo, la trisección de un ángulo, la duplicación del cubo) está llena de anécdotas, pero lo cierto es que como consecuencia de ellos surgieron, por ejemplo, las
secciones cónicas, cálculo aproximado del número pi, el método de exhaución como predecesor del cálculo de límites o la introducción de curvas trascendentes. Asimismo, el surgimiento
de la irracionalidad condicionó la necesidad de creación de una teoría general de las relaciones, teoría cuyo fundamento inicial lo constituyó el algoritmo de Euclides.
THALES DE MILETO
Tales nació en la ciudad de Mileto una antigua ciudad en la
costa occidental de Asia Menor. Fue hijo de Euxamias y de
Cleobulina y al parecer tuvo ascendencia fenicia.
De los babilonios debió aprender astronomía. En su
¨Cronología¨, afirma que murió a la edad de setenta y ocho
años
SU VIDA

3.  En su juventud viajó a Egipto, donde aprendió
geometría de los sacerdotes de Menfis, y
astronomía, que posteriormente enseñaría con
el nombre de astrosofía.
 Fue maestro de Pitágoras y Anaxímedes, y
contemporáneo de Anaximandro
 Fue el primer filósofo griego que intentó dar
una explicación física del Universo, que para él
era un espacio racional pese a su aparente
desorden
 Sin embargo, no buscó un Creador en dicha
racionalidad, pues para él todo nacía del agua,
la cual era el elemento básico del que estaban
hechas todas las cosas, pues se constituye en
vapor, que es aire, nubes y éter; del agua se
forman los cuerpos sólidos al condensarse, y
la Tierra flota en ella.
SUS
ESTUDIOS
 Sus estudios lo condujeron a resolver ciertas
cuestiones como:
o La determinación de las distancias
inaccesibles
o La igualdad de los ángulos de la base
en el triangulo isósceles
o El valor del Angulo inscrito
o La demostración de los conocidos
teoremas que llevan su nombre
relativos a la proporcionalidad de
segmentos determinados en dos rectas
cortadas por un sistema de paralelas
SU
REPRESENTACIÓN
 Representa los comienzos de la geometría
como ciencia racional.
 Fue uno de los siete sabios y fundador de la
escuela jonica a la que pertenecieron
Anaximandro, Anaxagoras, etc.
 En su edad madura se dedico al estudio de
la filosofía y de las ciencias, especialmente
de la GEOMETRIA
PITAGORAS DE SAMOS

4. Pitágoras de Samos nació en la isla de Samos.
Siendo muy joven viajó a Mesopotamia y Egipto fue
un filósofo y matemático griego, famoso sobre todo
por el Teorema de Pitágoras, que en realidad
pertenece a la escuela pitagórica y no sólo al mismo
Pitágoras.
SU VIDA
 Pitágoras, nació en la isla de Samos
 Su escuela de pensamiento afirmaba que la
estructura del universo era aritmética y
geométrica, a partir de lo cual las matemáticas
se convirtieron en una disciplina fundamental
para toda investigación científica.
 Pitágoras pasa por ser el introductor de pesos
y medidas, y elaborador de la teoría musical;
el primero en hablar de "teoría" y de "filósofos",
en postular el vacío, en canalizar el fervor
religioso en fervor intelectual, en usar la
definición y en considerar que el universo es
una obra sólo descifrable a través de las
matemáticas.
SU
FUNDACION
 Se dice que fue discípulo de Tales , pero
apartándose de la escuela jonica, fundo Trotona,
Italia, la escuela pitagórica.
 Se le atribuye también a la escuela pitagórica:
o la demostración de la propiedad de la
suma de los ángulos internos
o la construcción geométrica del polígono
estrellado de cinco lados
o Fueron los pitagóricos los primeros en
sostener la forma esférica de la tierra y
postular que esta, el sol y el resto de los
planetas conocidos, no se encontraban en
el centro del universo, sino que giraban en
torno a una fuerza simbolizada por el
número uno.
TEOREMA
DE
PITAGORAS
En un triángulo rectángulo, el cuadrado de la hipotenusa
es igual a la suma de los cuadrados de los catetos.
Cada uno de los sumandos, representa el área de un
cuadrado de lado, a, b, c. Con lo que la expresión anterior,
en términos de áreas se expresa en la forma siguiente:
El área del cuadrado construido sobre la hipotenusa de un
triángulo rectángulo, es igual a la suma de las áreas de los
cuadrados construidos sobre los catetos.
EUCLIDES

5. Euclides vivió alrededor del año 300 a.C,
Matemático griego. Poco se conoce a ciencia cierta de la
biografía de Euclides, pese a ser el matemático más
famoso de la Antigüedad.
SU VIDA
 Su vida es poco conocida, salvo que vivió en
Alejandría, Egipto. Proclo, el último de los
grandes filósofos griegos, quien vivió alrededor
del 450 dC., es la principal fuente.
 Es probable que Euclides se educara en
Atenas, lo que explicaría con su buen
conocimiento de la geometría elaborada en la
escuela de Platón, aunque no parece que
estuviera familiarizado con las obras de
Aristóteles.
 Existen algunos otros datos poco fiables.
Algunos autores árabes afirman que Euclides
era hijo de Naucrates
OBRAS:
 Euclides fue autor de diversos tratados, pero
su nombre se asocia principalmente a uno de
ellos, los Elementos, que rivaliza por su
difusión con las obras más famosas de la
literatura universal, como la Biblia o el Quijote
 Euclides fue un personaje histórico que
escribió Los Elementos y otras obras
atribuidas a él.
 Euclides fue el líder de un equipo de
matemáticos que trabajaba en Alejandría.
Todos ellos contribuyeron a escribir las obras
completas de Euclides, incluso escribiendo
libros a nombre de Euclides después de su
muerte.
OTROS DATOS
DE SU VIDA:
 La tradición ha conservado una imagen de
Euclides como hombre de notable amabilidad y
modestia
 Enseñó en Alejandría, donde alcanzó un gran
prestigio en el ejercicio de su magisterio durante el
reinado de Tolomeo I Sóter; se cuenta que éste lo
requirió para que le mostrara un procedimiento
abreviado para acceder al conocimiento de las
matemáticas, a lo que Euclides repuso que no
existía una vía regia para llegar a la geometría
 Euclides construye la geometría partir de
definiciones, postulados y axiomas con los cuales
demuestra teoremas que, a su vez, le sirven para
demostrar otros teoremas

6. PLATÓN
Platón fue un filósofo griego, alumno de Sócrates y
maestro de Aristóteles, de familia nobilísima y de la más
alta aristocracia. Su influencia como autor y
sistematizador ha sido incalculable en toda la historia de
la filosofía,
SU VIDA
 Nacido en el seno de una familia aristocrática,
abandonó su vocación política por la Filosofía,
atraído por Sócrates.
 Siguió a éste durante veinte años y se enfrentó
abiertamente a los sofistas (Protágoras,
Gorgias…). Tras la muerte de Sócrates (399 a.
C.), se apartó completamente de la política; no
obstante, los temas políticos ocuparon siempre
un lugar central en su pensamiento, y llegó a
concebir un modelo ideal de Estado.
 Viajó por Oriente y el sur de Italia, donde entró
en contacto con los discípulos de Pitágoras;
luego pasó algún tiempo prisionero de unos
piratas, hasta que fue rescatado y pudo
regresar a Atenas.
FUE FUNDADOR
DE:
 Fue fundador de la Academia de Atenas, donde estudió
Aristóteles. Participó activamente en la enseñanza de la
Academia y escribió sobre diversos temas filosóficos,
especialmente los que trataban de la política, ética, metafísica
y epistemología.
 Se opuso a las aplicaciones de Geometría pues para el la
matematica no tiene como finalidad la practica sino la
cultivación de esta con el unico fin de conocer
 La geometría la dividio en elemental y superior
o La Geometría Elemental comprendia todos los
problemas que se podian resolver con regla y
compas
o Y la Geometría Superior estudiaba los tres
problemas mas famosos de la Geometría
Antigua
- La Cuadratura del Circulo
- La trisección del angulo
- La duplicación del cubo
OBRAS:
 A diferencia de Sócrates, que no dejó obra
escrita, los trabajos de Platón se han
conservado casi completos y se le considera
por ello el fundador de la Filosofía académica
 El contenido de estos escritos es una
especulación metafísica, pero con evidente
orientación práctica. El mundo del verdadero
ser es el de las ideas, mientras que el mundo
de las apariencias que nos rodean está
sometido a continuo cambio y degeneración.

7. ARQUIMEDES DE
SARACUSA
Arquímedes matemático y geómetro griego considerado
el más notable científico y matemático de la antigüedad,
es recordado por el Principio de Arquímedes y por sus
aportes a la cuadratura del círculo
SU VIDA
 Matemático griego. Hijo de Fidias un
astrónomo, quien probablemente le introdujo
en las matemáticas
 Arquímedes estudió en Alejandría, donde tuvo
como maestro a Conón de Samos y entró en
contacto con Eratóstenes; a este último dedicó
Arquímedes su Método, en el que expuso su
genial aplicación de la mecánica a la
geometría, en la que «pesaba»
imaginariamente áreas y volúmenes
desconocidos para determinar su valor.
 De la biografía de Arquímedes, gran
matemático e ingeniero, a quien Plutarco
atribuyó una «inteligencia sobrehumana», sólo
se conocen una serie de anécdotas.
OTROS DATOS
DE SU VIDA
 Se encuentra en el una mentalidad practica, un genio
técnico, que lo llevo a investigar problemas de orden
físico y resolverlos por métodos nuevos
 Por esto después de grandes disputas con los
euclidianos se retiro a Siracusa donde puso sus
descubrimientos al servicio de la técnica.
 La obra Sobre la esfera y el cilindro, fue su teorema
favorito, que por expreso deseo suyo se grabó sobre
su tumba.
 Son célebres los ingenios bélicos cuya paternidad le
atribuye la tradición y que, según se dice, permitieron
a Siracusa resistir tres años el asedio romano, antes
de caer en manos de las tropas de Marcelo; también
se cuenta que, contraviniendo órdenes expresas del
general romano, un soldado mató a Arquímedes por
resistirse éste a abandonar la resolución de un
problema matemático en el que estaba inmerso,
escena perpetuada en un mosaico hallado en
Herculano.
DESCUBRIMIENTOS
 Calculo:
o Un valor más aproximado de π (pi)
o El volumen del cono , de la esfera
o el estudio de la palanca
o el tornillo de Arquímedes
o la Arquímedes que sirve para la
trisección del Angulo y otros aportes a
la matemática, la ingeniería y la
geometría.

8. HERÓN DE
ALEJANDRIA
Herón de Alejandría (c. 20-62 d.C.), matemático y
científico griego. Su nombre también podría ser Hero
(aproximadamente 18 escritores griegos se llamaron Hero
ó Herón, creándose cierta dificultad a la hora de su
identificación).
SU VIDA
 Herón de Alejandría nació probablemente en
Egipto y realizó su trabajo en Alejandría
(Egipto).
 Después de que desapareció el Imperio
Alejandrino y con él la ciencia griega, todavía
existieron algunos destellos de genialidad. Uno
de estos genios fue Herón, que desplegó una
actitud casi moderna para la mecánica
 Sin embargo, es conocido sobre todo como
matemático tanto en el campo de la geometría
como en el de la geodesia (una rama de las
matemáticas que se encarga de la
determinación del tamaño y configuración de la
Tierra, y de la ubicación de áreas concretas de
la misma).
SUS OBRAS:
 Escribió al menos 13 obras sobre mecánica,
matemáticas y física.
 En lo referente a la óptica, Herón, en su
libro Catóptrico, propuso que la luz viaja a lo
largo del camino geométricamente más
corto. Hoy se sabe que esto es falso, según
el principio de Fermat.
 En otro libro, Neumática, describe el diseño
de sifones, de máquinas que funcionan con
monedas y del aelopilo, que vendría a ser el
equivalente de una turbina de vapor
 Estudió la reflexión de la luz en espejos de
distinta forma.
DESCUBRIMIENTOS
 Sus principales descubrimientos son:
o demostró que el angulo de incidencia es igual al de
reflexión, conocido como Ley fundamental de la reflexión.
o Describió un gran número de máquinas sencillas y
generalizó el principio de la palanca de Arquímedes.
o Sin olvidar que realizó grandes trabajos, hizo numerables
innovaciones en el campo de los autómatas, incluyendo
uno el cual debería de hablar.
o Su mayor logro es la invención la primera máquina de
vapor, conocida como eolípila y la fuente de Herón.
o Encuentra diferentes maneras de hallar el área de
triángulos, cuadriláteros, polígonos regulares de tres a
doce lados, círculos, elipses y superficies y volúmenes de
cilindros, conos y esferas.