limite infinito

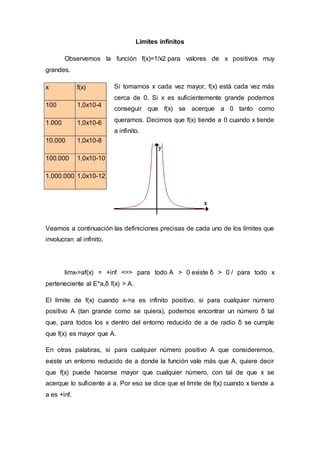
1. Limites infinitos
Observemos la función f(x)=1/x2 para valores de x positivos muy
grandes.
Si tomamos x cada vez mayor, f(x) está cada vez más
cerca de 0. Si x es suficientemente grande podemos
conseguir que f(x) se acerque a 0 tanto como
queramos. Decimos que f(x) tiende a 0 cuando x tiende
a infinito.
Veamos a continuación las definiciones precisas de cada uno de los límites que
involucran al infinito.
limx->af(x) = +inf <=> para todo A > 0 existe δ > 0 / para todo x
perteneciente al E*a,δ f(x) > A.
El límite de f(x) cuando x->a es infinito positivo, si para cualquier número
positivo A (tan grande como se quiera), podemos encontrar un número δ tal
que, para todos los x dentro del entorno reducido de a de radio δ se cumple
que f(x) es mayor que A.
En otras palabras, si para cualquier número positivo A que consideremos,
existe un entorno reducido de a donde la función vale más que A, quiere decir
que f(x) puede hacerse mayor que cualquier número, con tal de que x se
acerque lo suficiente a a. Por eso se dice que el límite de f(x) cuando x tiende a
a es +inf.
x f(x)
100 1,0x10-4
1.000 1,0x10-6
10.000 1,0x10-8
100.000 1,0x10-10
1.000.000 1,0x10-12

2. Limite unilateral por la derecha y por la izquierda.
Hasta el momento hemos visto límites de funciones cuyo trazo es
continuo, sin cortes o saltos bruscos. Sin embargo, existen algunas funciones
que presentan algunas discontinuidades, llamadas funciones discontinuas y
que estudiaremos en el tema continuidad de funciones. Nos dedicaremos ahora
a estudiar los límites que corresponde en este tipo de funciones como tal.
Consideremos la siguiente representación gráfica de una función , en la que
existe una discontinuidad cuando :
notemos que cuando tiende
hacia "a" por la derecha de "a" la
función tiende a 2, pero
cuando tiende hacia "a" por la
izquierda de "a", la función tiende
hacia 1.
Escribimos para indicar que tiende hacia "a" por la derecha, es decir,
tomando valores mayores que "a". Similarmente indica que tiende
hacia "a" por la izquierda, o sea, tomando valores menores que "a". Utilizando
ahora la notación de límites, escribimos y . Estos
límites reciben el nombre de límites laterales; el límite por la derecha es 2 y el
límite por la izquierda es 1.

3. Ejemplo:
Determinaremos los límites en los puntos de discontinuidad de la
función cuya representación gráfica es la siguiente:
Se tiene
que:
y
y
Definiciónde límiteporla
derecha
Se dice que si y solosi para
cada existe tal que
si entonces esel límite
por la derechade en"a".

4. Observe que no hay barras de valor absoluto alrededor de , pues es
mayor que cero ya que .
Definición de límite por la izquierda
Se dice que si y solo si para cada existe tal
que si entonces es el límite por la
izquierda de en "a".
Note que la expresión es mayor que cero, pues por lo que .
En adelante determinaremos los límites laterales a partir de la representación
gráfica de una función cuya ecuación se da.
Ejemplo:
Determinar los límites, en los puntos de discontinuidad, de la función definida
por:

5. Primero hagamos la gráfica de la función:
El punto de discontinuidad se presenta cuando
Luego: y
Observe que el límite por la derecha (3), es diferente al límite por la izquierda
(2).
Límite infinito (+).
La idea intutitiva de esta situación nos decía que cuando x se hace muy grande
(o muy pequeño, respectivamente), f(x) va creciendo indefinidamente, es decir,
podemos hacer que f(x) sea tan grande como se quiera sin más que hacer que
x crezca o decrezca lo suficiente.
De nuevo nos encontramos con conceptos algo ambiguos: "hacerse pequeño"
y "hacerse grande". Al igual que en el caso anterior la cuestión principal es ¿a
partir de qué valor consideramos que un número es grande o pequeño?. Para
responder a esta pregunta procederemos igual que en la situación anterior, es
decir, partiremos de una situación concreta sobre la que se plantean una serie

6. de cuestiones. Las respuestas a estas cuestiones nos permitirán definir con
claridad los conceptos antes mencionados.
Límite infinito(-)
La idea intutitiva de esta situación nos decía que cuando x se hace muy grande
(o muy pequeño, respectivamente), f(x) va decreciendo indefinidamente, es
decir, podemos hacer que f(x) sea tan pequeño como se quiera sin más que
hacer que x crezca (o decrezca) lo suficiente.
De nuevo nos encontramos con conceptos algo ambiguos: "hacerse pequeño"
y "hacerse grande". Al igual que en el caso anterior la cuestión principal es ¿a
partir de qué valor consideramos que un número es grande o pequeño?. Para
responder a esta pregunta procederemos igual que en la situación anterior, es
decir, partiremos de una situación concreta sobre la que se plantean una serie
de cuestiones. Las respuestas a estas cuestiones nos permitirán definir con
claridad los conceptos antes mencionados.
Ejemplos

8. Niedlinger gil 19165784