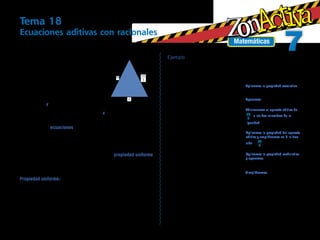
1. Tema 18
7
Ecuaciones aditivas con racionales
Matemáticas
Ejemplo
El perímetro del triángulo isósceles,
Hallemos el valor de la longitud del tercer lado del triángulo de
en la figura de la derecha mide 43
la figura.
m. Los lados congruentes miden 6 10 m 10 m
10 m cada uno. ¿Cuál es la longi- 3 3
3 10 + 10 + x = 43 Aplicamos la propiedad asociativa.
tud del tercer lado? 3 3 6
x 20 + x = 43 Operamos.
Si llamamos x a la longitud desconocida, podemos modelar el 3 6
Adicionamos el opuesto aditivo de
problema con la expresión: 10 + 10 + x = 43 que es una igual- 20 a los dos miembros de la
3 3 6 20 + − 20 + x = 43 + − 20 3
dad en la que aparece un término desconocido. Estas igualdades 3 3 6 3 igualdad.
se denominan ecuaciones.
Aplicamos la propiedad del opuesto
Plantear ecuaciones es una estrategia que se usa para hallar la
0 + x = 43 − 40
aditivo y amplificamos en 2 la frac-
solución de un problema. 6 6 ción − 20 .
3
Las propiedades de las operaciones estudiadas anteriormente,
junto con la siguiente propiedad denominada propiedad uniforme x = 3
Aplicamos la propiedad modulativa
y operamos.
de la adición, sustracción, multiplicación y división son muy útiles 6
para hallar la solución de una ecuación.
x = 1 Simplificamos.
2
Propiedad uniforme: si en ambos miembros de una igualdad,
adicionamos, sustraemos o multiplicamos por el mismo número,
la igualdad se conserva. Lo mismo sucede si dividimos ambos De esta manera, la solución de nuestra ecuación es 1 , es decir,
miembros por un mismo número diferente de cero. la longitud del tercer lado del triángulo es 1 m. 2
2