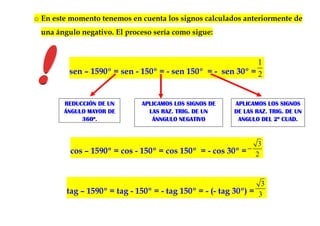
El documento describe los pasos para calcular las razones trigonométricas de ángulos en diferentes cuadrantes y situaciones. Explica cómo reducir ángulos mayores de 360° y negativos a ángulos equivalentes en el primer cuadrante, y aplicar los signos correctos de las razones trigonométricas en cada caso.

1. REDUCCIÓN DE UN ÁNGULO DEL 2º Cuad: AL 1º Cuad.
Calcula las razones trigonométricas de 150º
Seguimos el siguiente guión:
• Localizamos el cuadrante al que pertenece el ángulo; en este caso al SEGUNDO CUADRANTE.
• Anotamos los signos de las respectivas razones trigonométricas del cuadrante del ángulo
problema (α); en este caso (2º Cuad.) sen (+) ; cos ( - ) ; tag ( - )
• Transformamos el ángulo problema a otro ángulo (β) del PRIMER CUADRANTE; en este caso como
el ángulo problema (α) pertenece al SEGUNDO CUADRANTE, aplicamos: 180º - α = β. Como sigue:
180º - α = β 180º - 150º = β β = 30º
• A continuación a partir de las razones trigométricas de 30º (conocidas), podemos calcular las de 150º,
teniendo en cuenta los signos de las razones de 150º (2º Cuadrante):
1
o Sen 150º = sen 30º =
2
3
o Cos 150º = - cos 30º = −
2
3
o Tag 150º = - tag 30º = −
3

2. REDUCCIÓN DE UN ÁNGULO DEL 3º Cuad: AL 1º Cuad.
Calcula las razones trigonométricas de 225º
225º
Seguimos el siguiente guión:
• Localizamos el cuadrante al que pertenece el ángulo; en este caso al TERCER CUADRANTE.
• Anotamos los signos de las respectivas razones trigonométricas del cuadrante del ángulo
problema (α); en este caso (3º Cuad.) sen (-) ; cos ( - ) ; tag ( + )
• Transformamos el ángulo problema a otro ángulo (β) del PRIMER CUADRANTE; en este caso como
el ángulo problema (α) pertenece al TERCER CUADRANTE, aplicamos: α - 180º = β. Como sigue:
α - 180º = β 225º - α = β β = 45º
• A continuación a partir de las razones trigométricas de 45º (conocidas), podemos calcular las de 225º,
teniendo en cuenta los signos de las razones de 225º (3º Cuadrante):
2
o Sen 225º = - sen 45º = −
2
2
o Cos 225º = - cos 45º = −
2
o Tag 225º = tag 45º = 1

3. REDUCCIÓN DE UN ÁNGULO DEL 4º Cuad: AL 1º Cuad.
Calcula las razones trigonométricas de 300º
300º
Seguimos el siguiente guión:
• Localizamos el cuadrante al que pertenece el ángulo; en este caso al CUARTO CUADRANTE.
• Anotamos los signos de las respectivas razones trigonométricas del cuadrante del ángulo
problema (α); en este caso (4º Cuad.) sen (-) ; cos ( + ) ; tag ( - )
• Transformamos el ángulo problema a otro ángulo (β) del PRIMER CUADRANTE; en este caso como
el ángulo problema (α) pertenece al CUARTO CUADRANTE, aplicamos: 360º - α = β. Como sigue:
360º - α = β 360º - 300º = β β = 60º
• A continuación a partir de las razones trigométricas de 60º (conocidas), podemos calcular las de 300º,
teniendo en cuenta los signos de las razones de 300º (4º Cuadrante):
3
o Sen 300º = - sen 60º = −
2
1
o Cos 300º = cos 60º =
2
o Tag 300º = - tag 60º = − 3

4. ÁNGULOS MAYORES DE 360º
Calcula las razones trigonométricas de 1305º
305
Seguimos el siguiente guión:
• Transformamos, mediante una división entre 360º, el ángulo problema (α) , a
otro menor de 360º; para esto analizamos el resto de la división. En nuestro caso:
1305º : 360º Cociente = 3; Resto = 225.
• El cociente representa el número de vueltas completas realizadas por el ángulo;
EL RESTO ES EL VALOR DEL ÁNGULO EQUIVALENTE AL ÁNGULO
PROBLEMA (α); al ser equivalente sus razones trigonométricas son IGUALES
en valor y signo.
• Nuestro ángulo problema (α) se ha transformado en 225º. (α) = 225º. (A partir
de aquí corresponde a un caso resuelto…)
SIGUE

5. • Localizamos el cuadrante al que pertenece el ángulo; en este caso al TERCER CUADRANTE.
• Anotamos los signos de las respectivas razones trigonométricas del cuadrante del ángulo
problema (α); en este caso (3º Cuad.)
sen (-) ; cos ( - ) ; tag ( + )
• Transformamos el ángulo problema a otro ángulo (β) del PRIMER CUADRANTE; en este caso como
el ángulo problema (α) pertenece al TERCER CUADRANTE, aplicamos: α - 180º = β. Como sigue:
α - 180º = β 225º - α = β β = 45º
• A continuación a partir de las razones trigométricas de 45º (conocidas), podemos calcular las de 225º,
teniendo en cuenta los signos de las razones de 225º (3º Cuadrante):
2
Sen 1305º = Sen 225º = - sen 45º = −
2
2
º Cos 225º = - cos 45º = −
2
tag 1305º = Tag 225º = tag 45º = 1

6. ÁNGULOS NEGATIVOS
Calcula las razones trigonométricas de - 1590º
159
Seguimos el siguiente guión:
SIGUE
• Se trata de un ángulo negativo y mayor de 360º. En este caso resolveremos el ejercicio como sigue.
• PARTE 1: CALCULO DEL ÁNGULO MENOR DE 360º EQUIVALENTE AL ANGULO PROBLEMA (α).
o Transformamos el ángulo problema (α) mayor de 360º como sigue (igual que en el
ejercicio anterior):
o Transformamos, mediante una división entre 360º, el ángulo problema (α) , a otro
menor de 360º; para esto analizamos el resto de la división. En nuestro caso:
1590º : 360º Cociente = 4; Resto = 150
o El cociente representa el número de vueltas completas realizadas por el ángulo; EL
RESTO ES EL VALOR DEL ÁNGULO EQUIVALENTE AL ÁNGULO PROBLEMA
(α); al ser equivalente sus razones trigonométricas son IGUALES en valor y signo.
• Nuestro ángulo problema (α) se ha transformado en 150º. (α) = - 150º.

7. • PARTE 2: RELACIONAMOS LAS RAZ. TRIG. DE UN ÁNG. NEGATIVO CON LAS DE UNO POSITIVO:
o sen ( - α ) = - sen α sen – 1590º = sen - 150º = - sen 150º
o cos ( - α ) = cos α cos – 1590º = cos - 150º = cos 150º
o tag ( - α ) = - tag α tag – 1590º = tag - 150º = - tag 150º
o A partir de ahora hay que tener en cuenta los signos calculados de un ángulo
negativo, con los signos propios del cuadrante al que pertenece el ángulo
problema (α) , es decir, (α) = - 150º.
SIGUE

8. • PARTE 3: REDUCCIÓN DEL ÁNGULO PROBLEMA(α) A OTRO DEL PRIMER CUADRANTE (β):
o Reducidos 150º (el signo menos lo tendremos en cuenta mas adelante) a un ángulo
(β) del primer cuadrante (ya resulto en otro ejercicio):
o Localizamos el cuadrante al que pertenece el ángulo; en este caso al SEGUNDO
CUADRANTE.
o Anotamos los signos de las respectivas razones trigonométricas del cuadrante del
ángulo problema (α); en este caso (2º Cuad.) sen (+) ; cos ( - ) ; tag ( - )
o Transformamos el ángulo problema a otro ángulo (β) del PRIMER CUADRANTE; en
este caso como el ángulo problema (α) pertenece al SEGUNDO CUADRANTE,
aplicamos: 180º - α = β. Como sigue:
180º - α = β 180º - 150º = β β = 30º SIGUE
o A continuación a partir de las razones trigométricas de 30º (conocidas), podemos
calcular las de 150º, teniendo en cuenta los signos de las razones de 150º (2º
Cuadrante).

9. o En este momento tenemos en cuenta los signos calculados anteriormente de
una ángulo negativo. El proceso sería como sigue:
1
sen – 1590º = sen - 150º = - sen 150º = - sen 30º = 2
REDUCCIÓN DE UN APLICAMOS LOS SIGNOS DE APLICAMOS LOS SIGNOS
NGULO
ÁNGULO MAYOR DE LAS RAZ. TRIG. DE UN DE LAS RAZ. TRIG. DE UN
360º. ÁNNGULO NEGATIVO ANGULO DEL 2º CUAD.
3
−
cos – 1590º = cos - 150º = cos 150º = - cos 30º = 2
3
tag – 1590º = tag - 150º = - tag 150º = - (- tag 30º) = 3