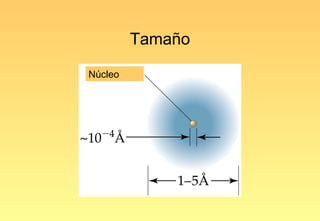
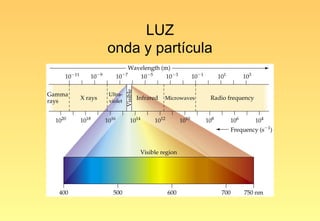
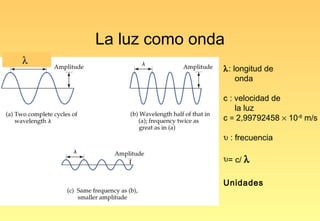
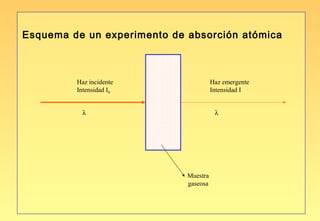
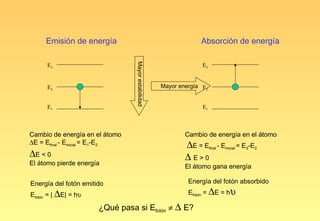
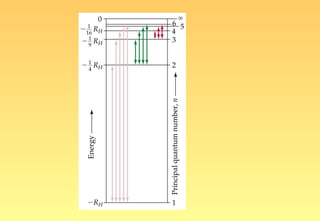
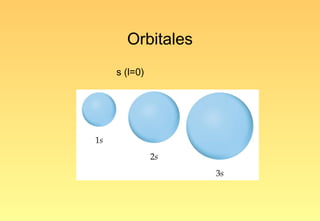
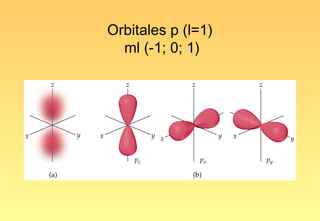
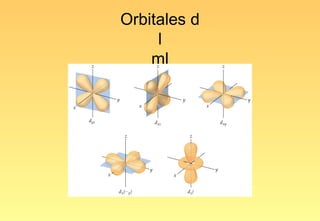
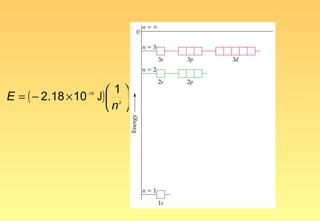
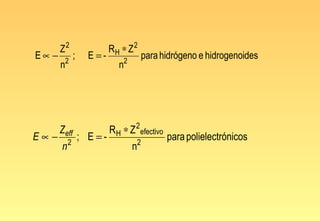
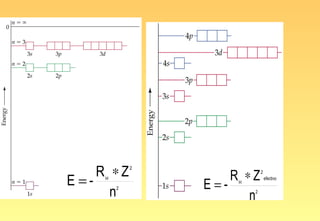
El documento resume la evolución del modelo atómico, desde los primeros modelos de Platón, Aristóteles y Demócrito, hasta el modelo actual basado en la mecánica cuántica. Explica las partículas subatómicas como el electrón y el protón, y cómo experimentos como el de Rutherford llevaron al modelo nuclear del átomo. También describe el comportamiento ondulatorio del electrón, el principio de incertidumbre de Heisenberg, y cómo la ecuación de Schrödinger explica los números cuánticos y los

1. Estructura de la materia
• Platón y Aristóteles: la materia es continua.
• Demócrito (470-370AC): la materia está formada por
átomos (partícula indivisible).
• Dalton (~ 1800):
- La materia esta formada por átomos.
- Elementos diferentes están formados por átomos diferentes.
- Los átomos no se crean ni se destruyen en las reacciones químicas.
- Los átomos se combinan en proporciones diferentes para formar
compuestos.

2. Estructura del átomo
• Thomson (1856-1940): electrón (1897)
• Millikan (1860 – 1953): carga del electrón
• Radiactividad (Becquerel).
• Thomson: modelo del budín.
• Rutherford (1871-1937): experimento de la placa de oro.
Modelo nuclear (1911)
• Rutherford (1919): protón.
• Chadwick (1932): neutrón.

3. Partículas subatómicas
Partícula Masa (uma) Masa Carga*
(gramos) (culombios)
Electrón 0,000549 9,1095 10-28 -1,6 10-19
(5,49 10-4)
Protón 1,00728 1,6726 10-24 1,6 10-19
Neutrón 1,00867 1,6750 10-24 0
* 1,6 10-19 Culombios = 1 unidad

4. Tamaño
Núcleo

5. A
X A : Número másico
Z : Número atómico
Z X : Símbolo químico
ISÓTOPOS: el mismo Z pero distinto A

6. Estructura electrónica de los átomos
• Interacción de la materia con la luz

7. LUZ
onda y partícula

8. La luz como onda
λ
λ: longitud de
onda
c : velocidad de
la luz
c = 2,99792458 × 10-8 m/s
υ : frecuencia
υ= c/ λ
Unidades

9. Planck: cuantización de la energía
• Radiación del cuerpo negro:
la energía sólo puede absorberse o liberarse en los átomos en
cantidades definidas llamadas cuantos.
• La relación entre la energía y la frecuencia de la radiación está
dada por:
E = hν
h es la constante de Planck (6.626 × 10-34 J.s).
(ejemplo: escalera vs rampa)

10. La luz como partícula
• Efecto fotoeléctrico (Einstein 1905): la luz está formada por
partículas, fotones.
Energía de un fotón:
E = hν

11. Esquema de un experimento de absorción atómica
Haz incidente Haz emergente
Intensidad I0 Intensidad I
λ λ
Muestra
gaseosa

14. Espectro visible
Espectro de emisión del átomo de hidrógeno en el visible
Espectro de absorción del átomo de hidrógeno en el visible

15. Espectros de líneas
• 1885. Balmer encontró que las líneas en la región visible del
espectro del hidrógeno responden a la siguiente ecuación:
1 1
ν = - RH ( 2
- 2
)
2 n
• Posteriormente Lyman generalizó esta expresión:
1 1 E = - RH (
1 1
ν = RH ( - ) -
2 n 2
)
n12 n2 2 n1 2
• Donde RH es la constante de Rydberg (3,29 1015 Hz)
• n1 y n2 son números naturales y distintos de cero (n2 > n1).

16. Espectro de emisión de diferentes átomos

17. Los espectros y el modelo atómico de
Bohr (1913)
• Rutherford asumió que los electrones están en órbitas alrededor del
núcleo (modelo planetario). Este modelo no explica los espectros de
líneas.
• Bohr considerando el concepto de cuantización de la energía
propone un nuevo modelo:
- los electrones describen órbitas circulares alrededor del núcleo.
- solamente están permitidas ciertas órbitas.
- los electrones no emiten ni absorben radiación mientras se
encuentren en una órbita permitida. Sólo hay emisión o radiación
cuando el electrón cambia de una órbita a otra permitida.

18. Emisión de energía Absorción de energía
Mayor estabilidad
E3 E3
E2 Mayor energía E2
E1 E1
Cambio de energía en el átomo Cambio de energía en el átomo
∆E = Efinal - Einicial = E1-E2 ∆E = E final - Einicial = E3-E2
∆E < 0 ∆ E>0
El átomo pierde energía El átomo gana energía
Energía del fotón emitido Energía del fotón absorbido
Efotón = | ∆E| = hυ Efotón = ∆E = hυ
¿Qué pasa si Efotón ≠ ∆ E?

19. • Como la energía está cuantizada, la luz emitida o
absorbida por un átomo aparece en el espectro como
una línea.
• Siguiendo una deducción matemática Bohr llega a la
conclusión (para hidrógeno):
 1
E = ( − 2.18 × 10 J)  
−18
n 
2
• n es el número de órbita (número cuántico principal).
n es natural (n=1, 2 , 3, …)

21. • La primer órbita en el modelo de Bohr corresponde a la órbita con
n=1. Es la más cercana al núcleo.
• Los electrones en el modelo de Bohr sólo se pueden mover entre
órbitas emitiendo o absorbiendo energía (cuantizada)
• Como se mencionara, la cantidad de energía absorbida o emitida
durante el movimiento de un electrón entre 2 órbitas está dada por:
∆E = E f − Ei = hν

22. Y entonces:
 1
∆E = hν =
hc
λ
( )
−18  1
= − 2.18 × 10 J 2 − 2 
n 
 f ni 
Si ni > nf, emisión de energía.
Si nf > ni, absorción de energía

23. Limitaciones del modelo de Bohr
• Sólo explica satisfactoriamente el espectro del hidrógeno (e iones
hidrogenoides, 1 electrón).

24. El comportamiento ondulatorio del
electrón
• Considerando las ecuaciones de Einstein y Planck, Louise de
Broglie (1924) demostró:
h
λ=
mv
de Broglie reúne los conceptos de onda y de partícula

25. El principio de incertidumbre
• Al considerar partículas con masas muy pequeñas (escalas atómicas) no
es posible determinar con suficiente precisión y simultáneamente su
posición y su velocidad (Heisemberg 1927).
h
∆x·∆mv ≥
4π
No tiene sentido describir el comportamiento del electrón en torno al núcleo
con las leyes de la mecánica clásica. Hay que considerar su comportamiento
como onda.

26. La ecuación de Schrödinger
• Es una ecuación que incluye las componentes ondulatorias. El movimiento de
una onda se describe matemáticamente mediante una ecuación que se
denomina ecuación de onda.
• Schrödinger describió el comportamiento del electrón girando alrededor del
núcleo como una onda y planteó la ecuación de onda.
• Al resolver matemáticamente esta ecuación se obtienen distintas soluciones
(estados del sistema).
• Para el átomo de hidrógeno existen infinitas soluciones de la ecuación de onda
(infinitos estados o estados electrónicos del sistema). Cada estado electrónico está
caracterizado por 4 números, los números cuánticos:
n, l, ml, ms

27. Números cuánticos
•n: principal 1, 2, 3,..., ∞.
Orbital •l: azimutal 0, 1,..., n-1.
•ml: magnético –l, -l+1,..., l-1, l.
•ms: spin –1/2, +1/2.
Los números cuánticos están relacionados don distintas propiedades de los
estados electrónicos.
La solución de la ecuación de Schrödinger muestra que para el átomo de
hidrógeno el estado caracterizado por el conjunto (n, l, ml, ms) tiene una
energía dada por:
R
E =- H
(para el hidrógeno)
n2

28. Orbitales
s (l=0)

29. Orbitales p (l=1)
ml (-1; 0; 1)

30. Orbitales d
l
ml

31. 1
E = ( − 2.18 × 10 J)  
−18
n 
2

32. Átomos polielectrónicos
• Modelo del campo medio: carga nuclear efectiva.
• La carga nuclear efectiva es la carga
experimentada por un electrón en un átomo
polielectrónico.
• La carga nuclear efectiva no es la misma que la
carga del núcleo por el efecto de los otros
electrones.

33. • Los electrones están atraidos por el núcleo, pero
repelidos por otros electrones.
• La carga nuclear efectiva experimentada por un
electrón depende de su distancia al núcleo y del
número de electrones del core.
Elemento Z efectivo* Z efectivo* Zefectivo*
(1s) (2s) (2p)
H (Z=1) 1,00
He (Z=2) 1,688
Li (Z=3) 2,691 1,279
B (Z=5) 4,680 2,576 2,421
* Calculado por reglas de Slater

34. Z2 RH ∗ Z 2
E∝− 2
; E =- 2
para hidrógeno e hidrogenoides
n n
Zeff R H ∗ Z 2 efectivo
E∝− 2
; E=- 2
para polielectrónicos
n n

35. R ∗Z 2
E =- H
n 2
R ∗Z 2
R ∗Z 2
E =- H
E=- H
efectivo
n 2
n2

36. Configuración electrónica
Configuración electrónica
indica en qué orbitales se encuentran los electrones.
Principio de Pauli
“en un átomo no puede haber dos electrones con los 4
números cuánticos iguales”.
Regla de Hund
“cuando se agregan electrones a una subcapa a medio
llenar, la configuración más estable es aquella que tiene
el mayor número de e- desapareados”.