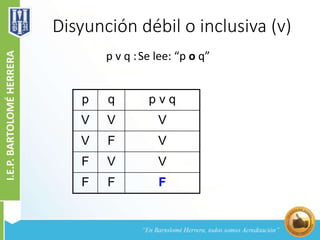
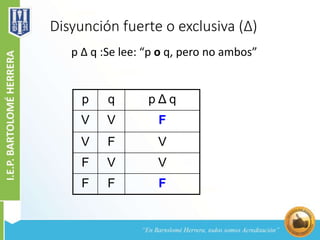
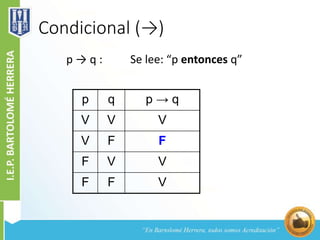
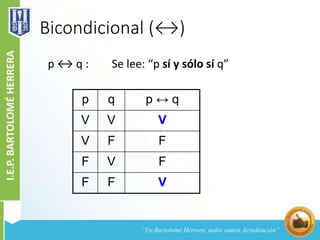
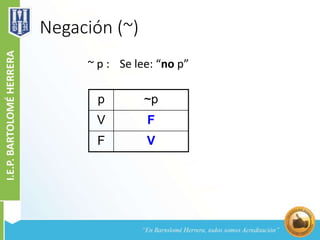
Este documento explica los conceptos básicos de la lógica proposicional, incluyendo enunciados, proposiciones, valores de verdad, variables proposicionales, conectores lógicos como la conjunción, disyunción, condicional y bicondicional, y tablas de verdad. Define cada uno de estos conceptos y provee ejemplos para ilustrar sus significados y valores de verdad.

1. ARITMÉTICA
“Lógica”
SECUNDARIA
4º

2. CAPACIDAD INDICADOR DE LOGRO
Interpreta conceptos
sobre lógica
mostrando interés en
todo momento.
Diferencia a los enunciados
de las proposiciones en un
cuadro de doble entrada.

3. Introducción
La lógica proposicional es la más antigua y simple de
las formas de lógica. Utilizando una representación
primitiva del lenguaje, permite representar y
manipular aserciones sobre el mundo que nos rodea.
Permite el razonamiento, a través de un mecanismo
que primero evalúa sentencias simples y luego
sentencias complejas, formadas mediante el uso de
conectivos proposicionales, por ejemplo Y, O,
Entonces, Si y sólo sí, etc.

4. Enunciado
Es toda oración, frase o expresión matemática.
Mi amiga Rosa es abogada.
¡Viva el Perú!
4 + 5 = 9

5. Proposición
Es aquel enunciado al que se le puede asignar un
valor ya sea de verdad o falsedad.
Hoy es miércoles.
3 x 5 = 8
Hace frío.

6. Valores Veritativos
Son los llamados valores de verdad. Es la
cualidad de una proposición de ser verdadera
(V) o falsa (F).
El profesor Figueroa enseña el curso de
Aritmética. ( V )
El profesor Velarde enseña el curso de
Psicología. ( F )

7. Variable Proposicional
Permite representar una proposición mediante una
letra del alfabeto.
Luis estudia inglés : p
Andrea siempre sonríe : q
45 x 9 = 405 : t
p, q , t : proposiciones simples

8. Conectores Lógicos
Se les llama también operadores lógicos.
Sirven para unir dos o más proposiciones.
Luis estudia inglés o Andrea siempre sonríe
p v q
(Proposición compuesta)

9. Tabla de verdad
Son reglas que determinan el valor veritativo de una
proposición compuesta, haciendo uso de conectores
lógicos.
Nº combinaciones = 2n
n: número de variables proposicionales

10. Conjunción (^)
p ^ q :Se lee: “p y q”
p q p ^ q
V V V
V F F
F V F
F F F

11. Disyunción débil o inclusiva (v)
p v q :Se lee: “p o q”
p q p v q
V V V
V F V
F V V
F F F

12. Disyunción fuerte o exclusiva (Δ)
p Δ q :Se lee: “p o q, pero no ambos”
p q p Δ q
V V F
V F V
F V V
F F F

13. Condicional (→)
p → q : Se lee: “p entonces q”
p q p → q
V V V
V F F
F V V
F F V

14. Bicondicional (↔)
p ↔ q : Se lee: “p sí y sólo sí q”
p q p ↔ q
V V V
V F F
F V F
F F V

15. Negación (~)
~ p : Se lee: “no p”
p ~p
V F
F V

16. Resumen
p q p ^ q p v q p Δ q p → q p ↔ q
V V V V F V V
V F F V V F F
F V F V V V F
F F F F F V V