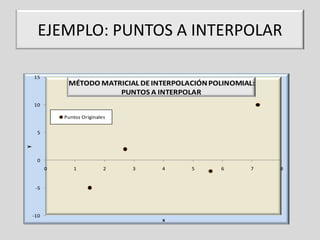
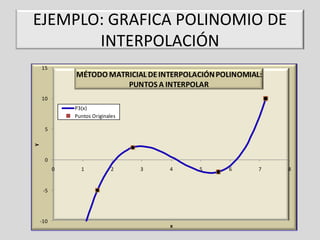
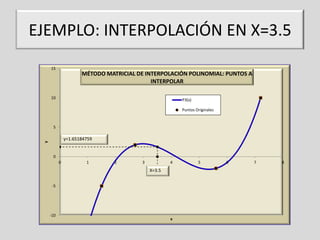
Este documento describe el método matricial para la interpolación polinómica. Explica cómo construir una matriz con los puntos de datos para obtener un sistema de ecuaciones lineales que permite calcular los coeficientes del polinomio de interpolación. También muestra un ejemplo numérico para hallar el polinomio de interpolación de Lagrange para un conjunto de puntos y estimar el valor de la función en un punto dado.

1. REGRESIÓN E INTERPOLACIÓN
MÉTODO MATRICIAL DE
INTERPOLACIÓN POLINOMIAL
MÉTODOS NUMÉRICOS

2. MÉTODO MATRICIAL DE
INTERPOLACIÓN POLINOMIAL
• La idea del método matricial es obtener la
ecuación del polinomio de interpolación, en la
forma
Pn  x   a0  a1 x  a2 x 2   an x n
• Teniendo como base que el polinomio de
interpolación debe satisfacer todos los puntos,
entonces

3. MÉTODO MATRICIAL DE
INTERPOLACIÓN POLINOMIAL
2
Pn  x0   a0  a1 x0  a2 x0 
Pn  x1   a0  a1 x1  a2 x12 
n
 an x0  y0
 an x1n  y1
2
Pn  x2   a0  a1 x2  a2 x2 
n
 an x2  y2
2
Pn  xn   a0  a1 xn  a2 xn 
n
 an xn  yn
• Matricialmente, se podría expresar como
1 x0

1 x1


1 xn

2
x0
x12
2
xn
n
x0   a0   y0 
    
x1n   a1   y1 


    
  
n 
xn   an   yn 

El cual corresponde a un
sistema de ecuaciones
lineales y se puede
resolver por cualquiera de
los métodos vistos

4. MÉTODO MATRICIAL DE
INTERPOLACIÓN POLINOMIAL
• Y si se establece que:
1 x0

1 x1
X


1 xn

 a0 
a 
a   1
 
 
 an 
2
0
2
1
x
x
2
xn
x 

x 

n
xn 

n
0
n
1
 y0 
y 
y   1
 
 
 yn 
Entonces, se
puede escribir
como:
Xa  y
Si se emplea el
método de la
inversa, se
obtendría
a  X 1 y

5. EJEMPLO
Halle el polinomio de interpolación de Lagrange
para el siguiente conjunto de puntos, y estime
el valor de la función para x=3.5 , utilizando este
polinomio
i
0
1
2
3
xi
1.5
2.7
5.6
7.2
f(xi)
-5
2
-2
10

6. EJEMPLO: PUNTOS A INTERPOLAR
15
MÉTODO MATRICIAL DE INTERPOLACIÓN POLINOMIAL:
PUNTOS A INTERPOLAR
10
Puntos Originales
y
5
0
0
1
2
3
4
-5
-10
x
5
6
7
8

7. MÉTODO MATRICIAL DE
INTERPOLACIÓN POLINOMIAL
• Para este caso n=3, entonces:
P3 1.5   a0  a11.5  a21.52  a31.53  5
P3  2.7   a0  a1 2.7  a2 2.7 2  a3 2.73  2
P3  5.6   a0  a1 5.6  a2 5.62  a3 5.63  2
P3  7.2   a0  a1 7.2  a2 7.22  a3 7.23  10

8. MÉTODO MATRICIAL DE
INTERPOLACIÓN POLINOMIAL
• Matricialmente quedaría:
1

1
1

1
1
1

1

1
1.5
2.7
5.6
7.2
1.52
2.7 2
5.62
7.22
1.53   a0   5
    
2.73   a1   2 


3
 a2   2 
5.6
  
3 
7.2   a3  10 
1.5 2.25
3.375   a0   5
2.7 7.29 19.683   a1   2 
    
5.6 31.36 175.616   a2   2 
    
7.2 51.84 373.248  a3  10 
1

1
X 
1

1
1.5
2.7
5.6
7.2
1.52
2.7 2
5.62
7.22
 a0 
a 
a   1
 a2 
 
 a3 
 5 
2
y 
 2 
 
10 
1.53 

2.73 
5.63 

7.23 

9. MÉTODO MATRICIAL DE
INTERPOLACIÓN POLINOMIAL
• El planteamiento para resolver este sistema
por el método de la inversa es el siguiente
1
1
a
1

1
1
1.5 2.25
3.375   5
2.7 7.29 19.683   2 
  
5.6 31.36 175.616   2 
  
7.2 51.84 373.248 10 
a  X 1 y
 3.88189987 3.86206897 1.53280067 0.55263158  5
 2.67008986 3.80076628 1.80246005 0.67178363   2 
 
a
 0.5527029 0.91315453 0.59924306 0.23879142  2

  
0.03565825 0.06385696 0.05256518 0.02436647  10 


10. MÉTODO MATRICIAL DE
INTERPOLACIÓN POLINOMIAL
• FINALMENTE SE OBTIENE:
P x   -35.7255544243282  31.2747382192515x  8.17622389775016 x 2  0.654800256411517 x3
3
Para hallar el valor del polinomio en x=3.5, simplemente se reemplaza este valor
en la expresión obtenida, con lo cual queda:
P 3.5  -35.7255544243282  31.2747382192515  3.5  8.17622389775016  3.5  0.654800256411517  3.5
3
2
P 3.5  1.65184758925629
3
3

11. EJEMPLO: GRAFICA POLINOMIO DE
INTERPOLACIÓN
15
MÉTODO MATRICIAL DE INTERPOLACIÓN POLINOMIAL:
PUNTOS A INTERPOLAR
10
P3(x)
Puntos Originales
y
5
0
0
1
2
3
4
-5
-10
x
5
6
7
8

12. EJEMPLO: INTERPOLACIÓN EN X=3.5
15
MÉTODO MATRICIAL DE INTERPOLACIÓN POLINOMIAL: PUNTOS A
INTERPOLAR
10
P3(x)
Puntos Originales
5
y
y=1.65184759
0
0
1
2
3
4
X=3.5
-5
-10
x
5
6
7
8