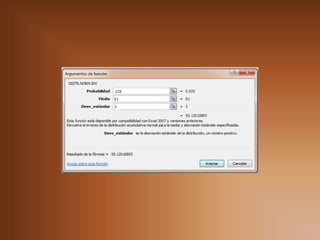
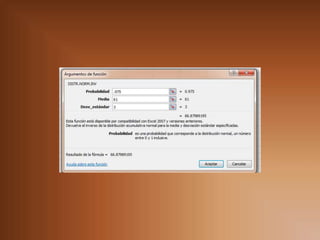
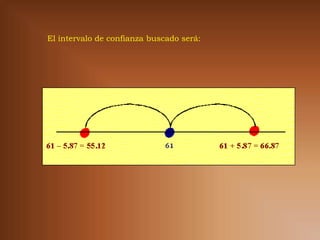
Este documento explica conceptos estadísticos como estimadores, error estándar, intervalos de confianza. Define un estimador como un estadístico que depende de la muestra para predecir un parámetro poblacional. Explica cómo calcular el error estándar para estimadores de la media, proporciones y varianzas. También describe cómo construir intervalos de confianza para la media usando el error estándar cuando se conoce la varianza poblacional.

1. Instituto Tecnológico Superior de
Zacapoaxtla
Departamento de Desarrollo
Académico
María del Consuelo Valle Espinosa

3. Un estimador es un estadístico cuyos valores dependen de la
muestra particular extraída. Se utiliza el valor del estimador,
llamado valor estimado, para predecir un valor de un
parámetro poblacional de interés.
Un estimador cuyo valor esperado coincide con el
parámetro que se desea estimar se dice que es un
estimador insesgado de dicho parámetro
El error estándar es la desviación estándar de la distribución
muestral.
El error estándar proporcionan una medida sobra la
incertidumbre de los datos contenidos en la muestra

5. Denotemos X1, … , Xn como una muestra extraída de una
población cuya media µ es desconocida, se puede utilizar la
media muestral como estimador de la media poblacional debido
a que:

E[ X ]  
La desviación estándar de la distribución de muestre o es:
   
SD  X  
  n
También conocida como error estándar del estimador de la
media poblacional .

6. Ejemplo:
Par un mismo individuo se han de realizar distintas mediciones de
su nivel de potasio en la sangre debido tanto a la imprecisión del
procedimiento de medición como al hecho de que el nivel real varia.
Se sabe que sus niveles de potasio varían alrededor de un valor
medio µ con una desviación estándar de 0.3, con los siguientes
datos estime su nivel medio.
3 .6  3 .9  3 .4  3 .5
 3 .6
4
El error estándar de este estimador es:
    0 .3
SD  X     0 . 15
  n 2
Por consiguiente, se puede tener una confianza en el que el valor de
la media no difiera de 3.6 en más de 0.3.
Si se quiere que el estimador tenga un error estándar de 0.05. Esto
supone dividir el error estándar por 3, y por ello se debe extraer
una muestra con un tamaño 9 veces mayor. Esto es se debe
realizar 36 mediciones.

8. Supongamos que se intenta estimar la proporción de
individuos que están a favor de una determinada propuesta.
Denotemos por p a dicha proporción desconocida ,
seleccionemos una muestra aleatoria, entonces:

X
p 
n
Siendo X el número de individuos de la muestra a favor de la
propuesta y n el tamaño de la muestra, el error estándar de
este estimador es:
 p (1  p )
SD  p  
  n

9. Si la media de una población µ es conocida, el estimador
apropiado de la varianza poblacional es:
n
  Xi   
2
i 1
n
Cuando por el contrario, si la media de la población es
desconocida, el estimado apropiado es:
2

 
n
  Xi  X 
i 1  
n 1

10. Una estimación por intervalo de un parámetro
poblacional es un intervalo para el que se predice que
el parámetro está contenido en él. La confianza que se
da al intervalo es la probabilidad de que el intervalo
contenga al parámetro.

11. Intervalo para la media si se
conoce la varianza
Este caso que planteamos es más a nivel teórico que
práctico: difícilmente vamos a poder conocer con
exactitud la varianza poblacional mientras que μ es
desconocida.
Sin embargo nos sirve para introducir el método que
permite estimar el intervalo de confianza para las medias.

12. Por el Teorema Central de Límite sabemos que mientras
el tamaño de la muestra implicada sea grande y se
conozca la varianza poblacional, la media de los datos
obtenidos de las muestras asume una distribución de
probabilidad normal, con media, la media poblacional y
varianza, la varianza poblacional dividida entre el
tamaño de la muestra.
Con la media muestral se puede construir un intervalo
de confianza de la media poblacional µ con un grado de
certidumbre asociado del (1- α)%.
Es decir, la media muestral es un estimador, tal que
haciendo un muestreo repetidamente y aleatoriamente a
la población se espera que el (1- α)% de los intervalos
numéricos generados contengan µ , eventualmente el α%
no lo hará.

13. Ejemplo:
Se sabe que una estimación puntual no sesgada de µ es 61.
Supóngase que por experiencias anteriores se sabe que X está
normalmente distribuida, con desviación estándar de 3. Se
quiere construir un intervalo de confianza al 95%
1. Consideremos la partición de la curva normal representada
en la siguiente figura.

14. 2. Calculemos los valores en el dominio de la función que
permiten tener áreas bajo la curva normal de .025 y .975

17. El intervalo de confianza buscado será:

18. Se ha construido un intervalo, de tal forma que podemos
confiar en un 95 % que la media poblacional está contenida
en él.

19. Referencia:
ESTADISTICA PARA BIOLOGIA Y CIENCIAS DE LA SALUD
J.SUSAN MILTON
MCGRAW-HILL / INTERAMERICANA DE ESPAÑA, S.A.,
2007
ISBN 9788448159962