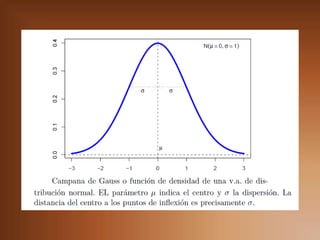
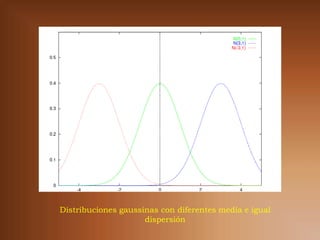
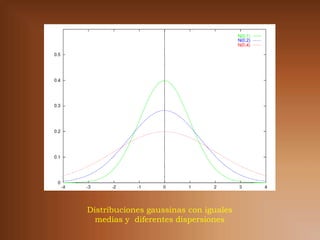
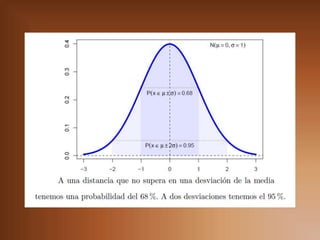
Este documento presenta información sobre distribuciones de probabilidad continua como la distribución exponencial y normal. Explica conceptos clave como función de densidad de probabilidad y cómo calcular probabilidades para valores de una variable aleatoria continua. También describe características específicas de la distribución normal como la regla de aproximación de tres sigmas y cómo calcular probabilidades para una distribución normal estándar. Finalmente, incluye ejemplos numéricos y referencias bibliográficas.

1. Instituto Tecnológico Superior de
Zacapoaxtla
Departamento de Desarrollo
Académico
María del Consuelo Valle Espinosa
 Distribución exponencial.
 Distribución Normal.

2. Una variable aleatoria es continua cuando todos sus
valores posibles forman un intervalo la recta real.
Toda variable aleatoria continua X tiene una curva
asociada a ella. Se puede utilizar esta curva,
formalmente conocida como la función de densidad de
probabilidad de la variable para obtener las
probabilidades referidas a X.
La probabilidad de que X tome un valor comprendido
entre a y b, siendo a menor que b como el área bajo la
curva dentro de este intervalo.
P[a ≤ X ≤ b = área bajo la curva entre a y b

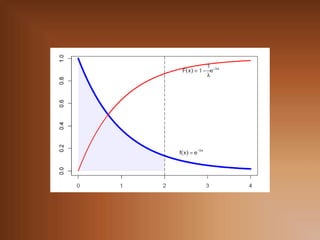
3. La función de densidad de probabilidad entere los punto a y
b es la misma se que los extremos a y b se incluyan o no.
P[a ≤ X ≤ b ] = P[a < X < b]
El área total bajo la curva de densidad debe de ser igual a
1.
La curva densidad nunca está debajo del eje x

9. Una variable aleatoria normal con media 0 y varianza 1 se denomina
normal estándar . Se usa la letra Z para denotarla

10. Distribuciones gaussinas con diferentes media e igual
dispersión

11. Distribuciones gaussinas con iguales
medias y diferentes dispersiones

13. Regla de aproximación
Una variable aleatoria normal con media µ y desviación
estándar σ estará:
Entre σ - µ y σ + µ con una probabilidad aproximada de
0.68
Entre σ - 2µ y σ + 2µ con una probabilidad aproximada de
0.95
Entre σ - 3µ y σ + 3µ con una probabilidad aproximada de
0.97
Esta regla de aproximación permite que nos hagamos una
idea sobre si un determinado conjunto de datos se aproxima
o no a una normal.

14. Ejemplo 1. Encuentre
P[ Z < 1.5]

15. .9331

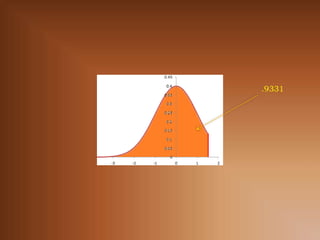
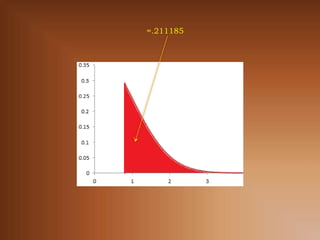
16. Ejercicio 2. Encuentre:
P[ Z ≥ .8]
P[ Z ≥ .8] = 1 - .788144601 = .211185

17. =.211185

18. Referencias:
Bioestadística: métodos y aplicaciones
Autores: Francisca Ríus Díaz, Francisco Javier Barón López,
Elisa Sánchez Font y Luis Parras Guijosa. Universidad de
Málaga .
Sitio en Internet:
http://www.bioestadistica.uma.es/libro/
INTRODUCCIÓN A LA ESTADÍSTICA
ROSS, SHELDON M. Editorial REVERTE