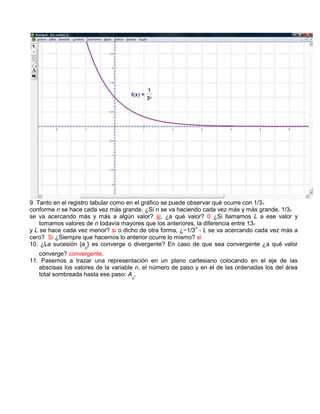
El documento describe un proceso en el que un cuadrado se divide recursivamente en rectángulos más pequeños, sombreando uno en cada paso. Con cada iteración, el área sombreada se aproxima más a 0.5 del área total. El área sombreada en el paso n se representa como an y tiende a 1/3 cuando n es grande. De igual forma, el área total acumulada An tiende a 0.5 cuando n es grande. Ambas sucesiones an y An convergen a estos valores respectivamente.

1. Actividad 2.
Un cuadrado de lado 1 cm. se divide en tres rectángulos iguales y se sombrea uno de ellos (paso
uno). Uno de los rectángulos no sombreados se divide en otros tres rectángulos iguales y se
sombrea uno de ellos (paso 2). Este proceso se continúa indefinidamente. A continuación te
presentamos los primeros seis pasos del proceso.
1. ¿Al terminar el primer paso qué valor tiene el área del rectángulo sombreado? =0.33
2. ¿En el segundo paso cuánta superficie se sombreó?
¿En total cuánta está sombreada? = = 0.4
3. ¿En el tercer paso cuánta superficie se sombreó?
¿En total cuánta está sombreada? = 0.481
4. ¿El total del área de la región sombreada se va a aproximando a un valor? si
De ser así, ¿a qué valor? A 0.5
5. Completa la tabla siguiente:
Área de la región en el paso:
Número de paso: n Área total: A
a. n
n
=0.3333
1

2. 2 = 0.4444
= 0.4814
3
= 0.4938
4
= 0.4979
5
6
= 0.4993
6. Generaliza y obtén una fórmula para a .
n
7. Para obtener la fórmula del área de la superficie en general, te proponemos que compruebes y
completes las siguientes sumas parciales: A1= a1=1/3 A2= a1+ a2= +
A3= a1+ a2 + a3 = + , A4 = ,... =An
Es conveniente que después de obtener la fórmula del área total, la verifiques para los valores de n
que encontraste en la tabla.
El área en cada paso, está dada por los términos de la sucesión infinita { an: }
a1= , a2= , a3= , a4=
cuyo término general es: { }
El área total en el proceso infinito, se puede expresar por medio de la serie:
a1+ a2 + a3 + a4 + ….. an = +
8. Coloca en el eje de las abscisas los valores de la variable n, el número de paso, y en el de las
ordenadas los del área en ese paso: a .
n

3. 9. Tanto en el registro tabular como en el gráfico se puede observar qué ocurre con 1/3 n
conforme n se hace cada vez más grande. ¿Si n se va haciendo cada vez más y más grande, 1/3n
se va acercando más y más a algún valor? si, ¿a qué valor? 0 ¿Si llamamos L a ese valor y
tomamos valores de n todavía mayores que los anteriores, la diferencia entre 13n
y L se hace cada vez menor? si o dicho de otra forma, ¿−1/3n - L se va acercando cada vez más a
cero? Si ¿Siempre que hacemos lo anterior ocurre lo mismo? si
10. ¿La sucesión {a } es converge o divergente? En caso de que sea convergente ¿a qué valor
n
converge? convergente.
11. Pasemos a trazar una representación en un plano cartesiano colocando en el eje de las
abscisas los valores de la variable n, el número de paso y en el de las ordenadas los del área
total sombreada hasta ese paso: A ,
n

4. 12. También en este caso, tanto en el registro tabular como en el gráfico se puede observar qué
ocurre con An conforme n se hace cada vez más grande. ¿Si n se va haciendo cada vez más y
más grande An se va acercando más y más a algún valor? Si , ¿a qué valor? 0.5 ¿Si llamamos
L a ese valor y tomamos valores de n todavía mayores que los anteriores, la diferencia entre Sn
y L se hace cada vez menor, o dicho de otra forma, −nAL se va acercando cada vez más a
cero? si ¿Siempre que hacemos lo anterior ocurre lo mismo? si Por todo ello, →∞limAn ¿a qué es
igual ? tiende a 0.5
13. Verifica que el término general de la sucesión { An } es An = 3n -1
2 3n
3n -1 = 34 -1 = 81 -1 = 80 = .4938
2 3n 2 34 2 81 162
3n -1 = 35 -1 = 243 -1 = 242 = .4979
2 3n 2 35 2 243 486
3n -1 = 36 -1 = 729 -1 = 728 = .4993
2 3n 2 36 2 729 1458
14. Comprueba que lim n →∞A n = lim n →∞( ) = lim n →∞( ) y determina el resultado del
límite.

5. 3n -1 = 3n -1 = 1 - 1__
2 3n 2 3 n n
2 3 2 2 3n
15. ¿La sucesión {An} es converge o divergente?convergente En caso de que sea convergente
a qué valor converge 0.5.
Es claro que si n tiende a infinito, la variación de la expresión de la derecha esta generada por
la variación de , pero como el lim→∞ , podemos concluir que el
lim n →∞A = lim n →∞ ( )=
16. Si el área del cuadrado fuera K, cuál sería el valor del área sombreada al final del proceso?
El concepto de convergencia hace referencia a la propiedad que poseen algunas sucesiones
numéricas de tender a un límite. Este concepto es bien general y dependiendo de la naturaleza
del conjunto donde se encuentre definida la sucesión, puede adoptar varias formas.
Divergente es la desviación
PRESENTA:
SARAHY JOFFRE BARCENAS
Graficador: Se utilizo un software para graficar las funciones
Nombre: “Sketchpag” Software de Geometría Dinámica para explorar
matemáticas
Versión: 4.05