Incrustar presentación
Descargar para leer sin conexión

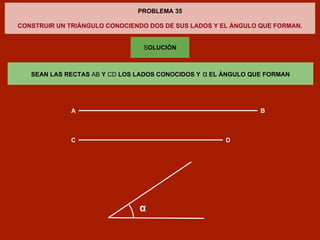




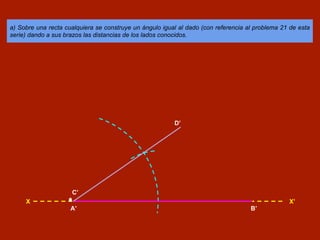
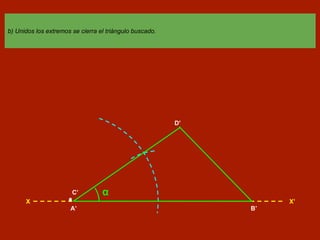

Este documento describe cómo construir un triángulo conociendo dos de sus lados y el ángulo que forman. Primero, se construye un ángulo igual al dado sobre una recta cualquiera, dando a sus brazos las distancias de los lados conocidos. Luego, se unen los extremos para cerrar el triángulo buscado.







