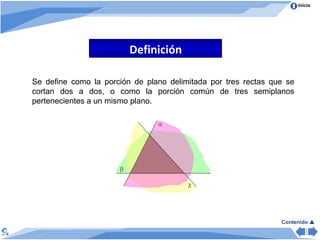
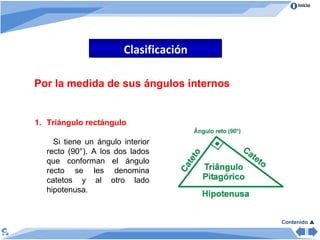
El documento presenta información sobre triángulos. Define el triángulo como una figura geométrica formada por tres segmentos que se unen de dos en dos. Explica los elementos, clasificaciones y propiedades de los triángulos, incluyendo la suma de sus ángulos internos y externos. También incluye ejercicios y recursos interactivos sobre triángulos.
Uso de los triángulos rectángulos, sus partes, hipotenusa y catetos, como poderlos referenciar desde un ángulo dado. Asimismo, poderlos identificar y ubicar dada la gráfica del triángulo rectángulo.
Esta presentación contiene algunos de los aspectos de los polígonos, incluyendo sus propiedades y algunos problemas de aplicación para aprender un poco más.
Uso de los triángulos rectángulos, sus partes, hipotenusa y catetos, como poderlos referenciar desde un ángulo dado. Asimismo, poderlos identificar y ubicar dada la gráfica del triángulo rectángulo.
Esta presentación contiene algunos de los aspectos de los polígonos, incluyendo sus propiedades y algunos problemas de aplicación para aprender un poco más.
Instrucciones del procedimiento para la oferta y la gestión conjunta del proceso de admisión a los centros públicos de primer ciclo de educación infantil de Pamplona para el curso 2024-2025.
1. Triángulos Prof. Jenny M. Portilla López MATEMÁTICA 1er grado de Secundaria Recursos Contenido Temático Presentación Evaluación Créditos Bibliografía Recursos Contenido Temático Contenido Temático Presentación Presentación Créditos
2. La geometría es una parte importante de la cultura del hombre, no es fácil encontrar contextos en que la geometría no aparezca de forma directa o indirecta. Actividades tan variadas como el deporte, la jardinería o la arquitectura por citar algunas se sirven de la utilización, consciente o no, de procedimientos geométricos. El triángulo es el polígono de menor número de lados, y a pesar de ello es el más importante, tanto por la gran cantidad de construcciones que se pueden plantear, como por tratarse de la figura que servirá de base para la construcción de otras más complejas, tanto planas como espaciales. Presentación
3. Contenido Temático Definición Elementos Clasificación Propiedades Taller de polígonos Ejercicios Ejercicio interactivo Video de ángulos
4. Definición Se define como la porción de plano delimitada por tres rectas que se cortan dos a dos, o como la porción común de tres semiplanos pertenecientes a un mismo plano. Contenido
5. Elementos Contenido A B C P Q R VÉRTICES: A, B, C LADOS: ELEMENTOS ASOCIADOS Ángulos internos : Ángulos externos: ABC; BCA y CAB PAB; QBC y RCA AB , BC , y AC
6. Clasificación Por la longitud de sus lados Triángulo equilátero Si sus tres lados tienen la misma longitud Triángulo isósceles Si tiene dos lados de la misma longitud. Triángulo escaleno Si todos sus lados tienen longitudes diferentes. Contenido
17. Recursos Rompecabezas Triángulos Panel Triángulos Pupiletras Triángulos Crucigrama Triángulos (Presiona click en uno de los recursos para ingresar)
